![]()
![]()
 开远一中高二数学测验答题卡
开远一中高二数学测验答题卡
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | C | B | C | D | A | B | A | C | D | C | D |
| 13题 0 14题 15题 16题 |
一.选择题(12×5=60
二.填空题(每题4分,共16分)
|
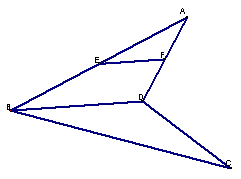
17、(12分) 证明:连结BD,在
又EF 平面BCD,
|
 三:解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.注意:以下所有解答均须填入方框内,否则不给分)
三:解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.注意:以下所有解答均须填入方框内,否则不给分)
| 18(12分)
而
即 |
|
证明:设
则
故EF,GH,KL共面。
|
|
|
证明:以D为坐标原点,DC为X轴的 正半轴,DA的反向延长线为Y轴的 正半轴, 如图所示的空间直角坐标系。 设正方体的边长为2a,则 D(0,0,0),A(0,2a,0) F(a,0,0)
(1)
(2)由
即 (3)由(1),(2)知
|
|
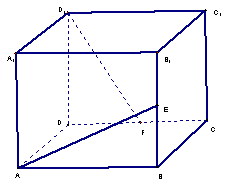
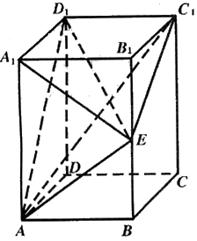 (1)长方体A—C1中,A1D1⊥面ABB1A1,∴A1D1⊥AE. 又AB=1,BB1=2,E为BB1中点, ∴△ABE为等腰直角三角形,AE= ∴∠AEA1=90°,即AE⊥A1E, ∴AE⊥平面A1D1E. (2)取AA1中点O,连OE,则OE⊥AA1,OE⊥A1D1, 于是OE⊥平面ADD1A1.过O作OF⊥AD1于F,连EF, 则AD1⊥EF. ∴∠EFO为二面角E—AD1—A1的平面角. △AOF中,OF=OA·sin∠OAF=OA·
故二面角E—AD1—A1的正切值是 (3)∵AB//C1D1,∴AB//平面C1D1E. ∴A点到平面C1D1E的距离等于B点到平面C1D1E的距离. 而A1—C是长方体,则平面C1D1E⊥平面BC1. 延长C1E与CB的延长线交于N,则平面C1D1E与平面BC1的交线为C1N. 过B在平面C1NC内作BM⊥C1N,垂直足为M,则BM的长就是B点到平面C1D1E的距离.依题意,得 故A点到平面C1D1E的距离为
|
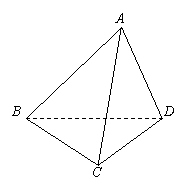 证明:
证明: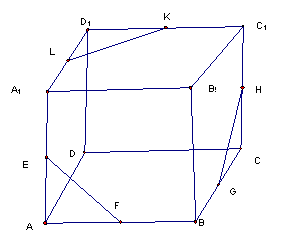 19(12分)
19(12分)
 21、(12分)
21、(12分)