.开远一中高二数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,总分共150分。考试时间为120分钟。注意:所有答案均需填入答题卡内,否则不给分！
第Ⅰ卷(选择题 共60分)
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．下列命题正确的是 （ ）
（A）三点可以确定一个平面 （B）一条直线和一个点可以确定一个平面
（C）三条直线两两相交可以确定一个平面 （D）空间不共线的四点最多可确定四个平面
2．三个互不重合的平面，能把空间分成n部分。则n的所有可能值为 （ ）
（A）4，6 （B）4，6，7 （C）4，6，7，8 （D）4，6，7，9
3．
（ ）
（A）-4 （B）9 （C）-9 （D）4
4．设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是 （ ）
A．
B．
C．
D．
5.分别和两条异面直线平行的两条直线的位置关系是 ( )
(A)平行 (B)相交 (C)异面 (D)相交或异面
6．如图，在平行六面体ABCD–A1B1C1D1中，M为AC
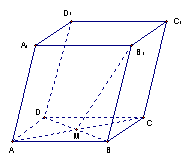与BD的交点.若
,
,
,则下列向
量中与
相等的向量是( )
（A）
（B）
（C）
（D）
7. 如图，点P在正方形ABCD所在平面外，PA⊥平面ABCD，PA=AB，
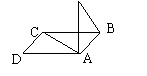则PB与AC所成的角是 （ ）
P
(A)90° (B)60° (C)45° (D)30°
8．已知二面角
的大小为
,如果平面
内一点A到平面
的距离为
,那么A在平面上的射影
到平面的距离是( )
(A)
（B）1 （C） （D）
9． 设有如下三个命题：
甲．两相交直线l，m都在平面内，并且都不在平面内；
乙．直线l，m中至少有一条与平面相交；
丙．平面与平面相交
当甲成立时 （ ）
A）乙是丙的充分但不必要条件； （B）乙是丙的必要但不充分条件；
（C）乙是丙的充要条件； （D）乙是丙的既不充分也不必要条件．
10．a，b表示不同的直线，
表示不同的平面，有下面四个命题：
①若
②若
③
④
上述四个命题中，正确的命题序号是 ( )
A．①④ B．①③ C．②④ D．④
11．给出下列四个命题：
①两条平行直线分别在两个平行平面内，则这两条平行线的距离等于这两个平面间的距离；
②两条异面直线分别在两个平行平面内，则这两条异面直线间的距离等于这两个平面间的距离；
③若平面α∥平面β，直线
，则直线a与平面β的距离等于平面α与平面β的距离。
④若平面α∥平面β，点
则点A到平面β的距离等于平面α与平面β的距离。
其中正确命题的个数是 ( )
A．1 B．2 C．3 D．4
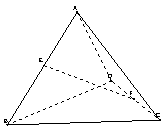12．如图。正四面体A-BCD中，E在棱AB上，F在棱CD上
，使得
，设
分别表示EF与AC，BD
所成的角，则 （ ）
（A）
上的增函数
（B） 
上的减函数
（C）
（D）
第Ⅱ卷(非选择题 共90分)
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.
13.已知
则x= .
14．若P是
所在平面外的一点,PB=PC=AB=AC,M是线段PA上一点,N线段BC的中点,则
.
15.
;类比上述性质得到一般性的结论是
16．正方体
中点,在对角面
上取一点M,使AM+AE最小,其最小值等于
.
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.
17.(12分)已知:空间四边形ABCD中,E,F分别是AB,AD中点(图见答题卡).求证:EF//平面ABCD.
18.(12分)已知(图见答题卡)四面体A－BCD中，AB⊥CD，AD⊥BC.
求证：AC⊥BD
19 (12)已知E,F,G,H,K,L分别为正方体AC1的棱AA1、AB、BC、CC1、C1D1、A1D1的中点,求证:EF,GH,KL三线共面.
20.(12分)如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上.
21. ( 12分)如图(图见答题卡)正方体ABCD–A1B1C1D1中,E、F分别是棱BB1、CD的中点. 证明(1)
(2)求AE与D1F所成的;
(3)证明: 面
22.. 如图（图见答题卡）在长方体ABCD—A1B1C1D1中，AB=BC=1，AA1=2，E是BB1的中点.
（1）求证：AE⊥平面A1D1E；
（2）求二面角E—AD1—A1的正切值；
（3）求顶点A到平面C1D1E的距离.