高二下 9.2 空间直线同步练习
基础练习
1.在正方体ABCD—![]() 中,共有12条棱,指出符合条件的棱所在的直线:
中,共有12条棱,指出符合条件的棱所在的直线:
(1)与直线AB平行的直线有_________;
(2)与直线AB相交的直线有_________;
(3)与直线AB异面的直线有____________________________________;
2.填空:正方体ABCD—![]() 各棱长为a,
各棱长为a,
(1)AC与![]() 的位置关系是_________,AC与
的位置关系是_________,AC与![]() 的位置关系是_________,AC与
的位置关系是_________,AC与![]() 的位置关系是_________;
的位置关系是_________;
(2) ![]() 与
与![]() 的位置关系是_________________,
的位置关系是_________________,![]() 与
与![]() 的大小关系是_________,△
的大小关系是_________,△![]() 与△
与△![]() 的关系是_________;
的关系是_________;
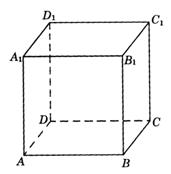
图9-9
(3)AB与![]() 所成的角是_________度,AB与
所成的角是_________度,AB与![]() 所成的角是_________度,
所成的角是_________度,![]() 与CD所成的角是_________度.
与CD所成的角是_________度.
3.指出图9-10中直线a、b的位置关系,其中:(2)中a∥l,且b∥l;(4)中a∥l;(5)中M∈a,N∈b,M∈b,N∈b.
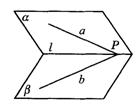
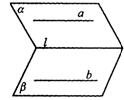
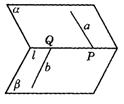
(1) (2) (3)
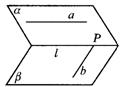
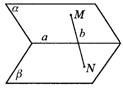
(4) (5)
图9-10
4.判断下列命题是否正确,并说明理由.
(1)空间两条直线可以确定一个平面;
(2)垂直于两条异面直线的直线有且只有一条;
(3)垂直于同一条直线的两条直线平行;
(4)直线a与b平行,b与c平行,则a与c平行;
(5)直线a与b相交,b与c相交,则a与c相交;
(6)直线a与b异面,b与c异面,则a与c异面;
(7)一条直线与两条平行线中的一条垂直,必和另一条也垂直.
5.a、b、l是三条直线,a、b是两个平面,且a∩b =l,a![]() a,b
a,b![]() b,则a与b的位置关系是_________.
b,则a与b的位置关系是_________.
6.直线a和b是平行直线,点A、C在直线a上,点B、D在直线b上,那么直线AB与CD的位置关系是什么?若直线a和b是异面直线呢?
7.在正方体ABCD—![]() 中,六个面内与BD所成的角为60°的对角线共有多少条?
中,六个面内与BD所成的角为60°的对角线共有多少条?
8.A、B、C、D是不在同一个平面内的四点.E是线段AD上一点.证明直线CE和BD是异面直线.
9.已知ABCD-![]() 为正方体,棱长为a.
为正方体,棱长为a.
(1)求异面直线![]() 与
与![]() 之间的距离;
之间的距离;
(2)若E、F分别为棱![]() 、AB的中点,求异面直线EF与
、AB的中点,求异面直线EF与![]() 之间的距离.
之间的距离.
综合练习
1.关于直线a、b有以下三个结论:
甲:a、b相交;乙:a、b平行;丙:a、b不是异面直线.
那么,下列命题中正确的是( ).
A.甲和乙均是丙的充分非必要条件
B.甲和乙均是丙的必要非充分条件
C.甲是丙的充分非必要条件,且乙是丙的必要非充分条件
D.甲是丙的必要非充分条件,且乙是丙的充分非必要条件
2.给出以下四个命题:
①若两条直线和第三条直线成等角,则这两条直线平行
②若两条直线和第三条直线都垂直,则这两条直线平行
③若两条直线都和第三条直线平行,则这两条直线平行
④若两条直线分别在两个相交平面内,则这两条直线不可能平行
其中错误命题的个数是( )个.
A.1 B.2 C.3 D.4
3.在正方体ABCD—![]() 中,与对角线
中,与对角线![]() 异面的棱有( ).
异面的棱有( ).
A.3条 B.4条 C.6条 D.8条
4.三条直线共面的条件可以是( ).
A.这三条直线两两平行B.这三条直线交于一点
C.这三条直线中的一条与另外两条都相交
D.这三条直线两两相交,但不交于一点
5.已知m、n为异面直线,m![]() 平面a,n
平面a,n![]() 平面b,a∩b=l,则l( ).
平面b,a∩b=l,则l( ).
A.与m、n都相交 B.与m、n中至少一条相交
C.与m、n都不相交 D.至多与m、n中的一条相交
6.如图9-11,在正方体ABCD—![]() 中,E、F分别是棱
中,E、F分别是棱![]() 、
、![]() 的中点,求证:EF∥BD,且
的中点,求证:EF∥BD,且![]() .
.
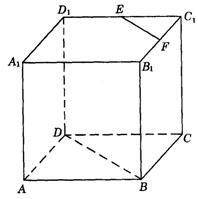
图9-11
7.如图9-12,O是平面ABC外一点,![]() 、
、![]() 、
、![]() 分别在线段OA、OB、OC上,且满足
分别在线段OA、OB、OC上,且满足![]() ,
,![]() .求证:△ABC∽△
.求证:△ABC∽△![]() .
.
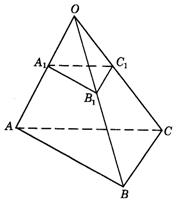
图9-12
8.如图9-13,P是平面ABC外一点,PA=4,![]() ,D、E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
,D、E分别为PC和AB的中点,且DE=3.求异面直线PA和BC所成角的大小.
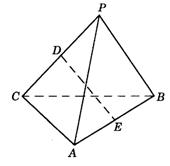
图9-13
9.如图9-14,A是平面BCD外一点,且AB=AC=DB=DC,M、N分别是BC、AD的中点.求证:MN是异面直线AD与BC的公垂线.
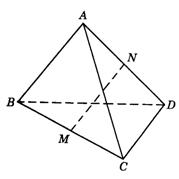
图9-14
10.如图9-15,已知A是平面BCD外一点,满足AC=BD,M、N、P、Q分别是BC、CD、DA、AB的中点.求证:QN⊥PM.
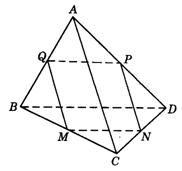
图9-15
11.如图9-16,在棱长为a的正方体ABCD—![]() 中,求异面直线AC和
中,求异面直线AC和![]() 的距离.
的距离.
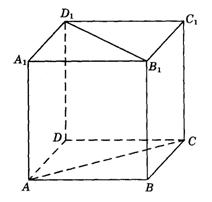
图9-16
12.在长方体ABCD-![]() 中,AB=2,
中,AB=2,![]() ,M、N分别是AD、DC的中点.
,M、N分别是AD、DC的中点.
(1)证明![]() ∥
∥![]() ;
;
(2)求异面直线MN与![]() 所成角的余弦值.
所成角的余弦值.
拓展练习
1.在空间四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,得到四边形EFGH.
(1)四边形EFGH是______________;
(2)当对角线AC=BD时,四边形EFGH是______________;
(3)当对角线满足条件______________时,四边形EFGH是矩形;
(4)当对角线AC、BD满足条件_______时,四边形EFGH是正方形.
2.借助两支铅笔,试研究以下问题:
(1)在平面内,过直线外一点有多少条直线与已知直线平行?在空间呢?
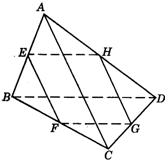
图9-17
(2)在一个平面内,过一点有多少条直线与已知直线垂直?在空间呢?
(3)在一个平面内,与该平面内的已知直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?在空间,与一条直线所成角为60°的直线有多少条?这些直线与已知直线的位置关系如何?
3.如图9-18,已知P为△ABC所在平面外一点,PC⊥AB,PC=AB=2,E、F分别为PA和BC的中点.
(1)求证:EF与PC是异面直线;
(2)EF与PC所成的角;
(3)线段EF的长.
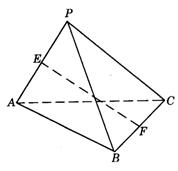
图9-18
4.如图9-19,在棱长为a的正方体ABCD—![]() 中,O是AC、BD的交点,E、F分别是AB与AD的中点.
中,O是AC、BD的交点,E、F分别是AB与AD的中点.
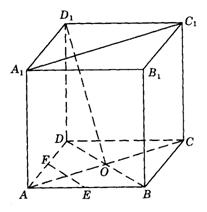
图9-19
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求异面直线EF与![]() 所成角的大小;
所成角的大小;
(3)求异面直线EF与![]() 所成角的正切值;
所成角的正切值;
(4)求异面直线EF与![]() 的距离.
的距离.
5.在空间中,
①若四点不共面,则这四点中任何三点都不共线.
②若两条直线没有公共点,则这两条直线是异面直线.
以上两个命题中,逆命题为真命题的是__________.
(把符合要求的命题序号都填上)
参考答案
基础练习
1.(1)AB∥DC∥![]() ∥
∥![]() ;(2)AD、
;(2)AD、![]() 、
、![]() 、BC;
、BC;
(3)![]() 、
、![]() 、
、![]() 、
、![]() .
.
2.(1)平行,异面,异面;(2)平行,相等,全等;(3)90,45,90.
3.(1)![]() =P;(2)a∥b(公理4);
=P;(2)a∥b(公理4);
(3)a与b是异面直线;(4)a与b是异面直线;(5)a与b是异面直线.
4.(1)不正确.两条异面直线不能确定一个平面.
(2)不正确.垂直于两条异面直线的直线有无数多条,但公垂线——与两条异面直线垂直相交的直线有且只有一条.
(3)不正确.垂直于同一直线的两条直线可能平行、相交或异面.
(4)正确.由公理4可知.
(5)不正确.a、c可能平行,还可能异面.
(6)不正确.a、c可能异面,但也可能平行或相交.
(7)正确.因为直线与两条平行线所成的角相等.
5.平行、相交或异面(参看图答9-10)
6.若a∥b,则a,b共面于a,A、B、C、D均在a内,故AB与CD共面于a,则AB与CD的位置关系可能是平行或相交.若a、b是异面直线,则AB与CD必是异面直线.假设AB与CD共面于b,则AC与BD,即a、b共面.这与已知矛盾.
7.参看图答9-10,与BD相交所成角为60°的面对角线![]() 、
、![]() ,
,![]() ,
,![]() 四条;与BD异面所成角为60°的面对角线有
四条;与BD异面所成角为60°的面对角线有![]() 、
、![]() 、
、![]() 、
、![]() 四条,故一共8条.
四条,故一共8条.
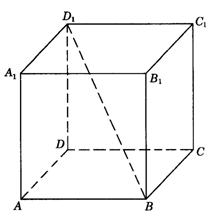
图答9-10
8.设CE、BD不是异面直线,那么CE、BD在同一个平面(设为a)内.由E、D在平面a 内,则直线ED在平面a内,直线ED上的点A也在平面a内,即A、B、C、D都在平面a内,这与A、B、C、D不在同一平面内是相矛盾的,因此CE、BD是异面直线.
9.(1)a(公垂线段为![]() );
);
(2)![]() (公垂线段为
(公垂线段为![]() ).
).
综合练习
1.A
2.C.根据公理4,知③正确,利用正方体判断其余命题均不正确.由![]() 与AB所成角90°,BC与AB所成的角90°,但
与AB所成角90°,BC与AB所成的角90°,但![]() 与BC不平行,从而①、②不正确;
与BC不平行,从而①、②不正确;![]() 在平面
在平面![]() 内,DC在平面ABCD内,虽平面
内,DC在平面ABCD内,虽平面![]() 与平面ABCD相交,仍有
与平面ABCD相交,仍有![]() ∥DC,从而说明④不正确.
∥DC,从而说明④不正确.
3.C.如图答9-10,把正方体的几条棱分为三类,在平面![]() 上的四条棱中有
上的四条棱中有![]() 、
、![]() 与
与![]() 异面,在平面ABCD上的四条棱中有AD、CD与
异面,在平面ABCD上的四条棱中有AD、CD与![]() 异面,上下两底面之间的四条棱中,有
异面,上下两底面之间的四条棱中,有![]() 、
、![]() 与
与![]() 是异面直线,故与
是异面直线,故与![]() 异面的棱共6条.
异面的棱共6条.
4.D.可参看下列图形:
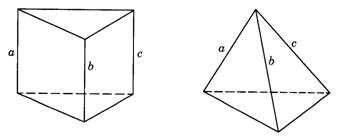
图答9-9
5.B.可参看下列图形:
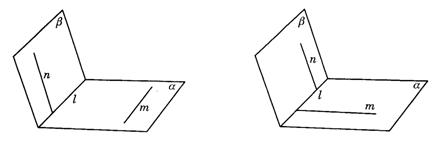
图答9-11
6.连结![]() .∵
.∵ ![]() ∥
∥![]() ,∴ 四边形
,∴ 四边形![]() 是平面图形,又∵
是平面图形,又∵![]() =
=![]() ,∴ 四边形
,∴ 四边形![]() 是平行四边形,∴ BD
是平行四边形,∴ BD![]()
![]() ,在△
,在△![]() 中,∵ E、F分别是
中,∵ E、F分别是![]() 与
与![]() 的中点,∴ EF
的中点,∴ EF![]()
![]() ,由公理4有EF∥BD,且有
,由公理4有EF∥BD,且有![]() .
.
7.∵
![]() ,
,![]() ,∴
,∴ ![]() .在△AOB中,由
.在△AOB中,由![]() ,∴
,∴ ![]() ∥AB,同理
∥AB,同理![]() ∥BC,∵
∥BC,∵
![]() 与∠ABC方向相同,∴
与∠ABC方向相同,∴
![]() =∠ABC,同理
=∠ABC,同理![]() =∠BAC,∴
△
=∠BAC,∴
△![]() ∽△ABC.
∽△ABC.
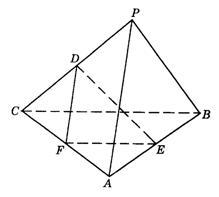
图答9-12
8.取AC中点F,连结DF、EF,在△PAC中,∵ D是PC中点,F是AC中点,则DF∥PA,同理可得EF∥BC,∴
∠DFE为异面直线PA与BC所成的角.在△DEF中,DE=3,又DF=![]() PA=2,EF=
PA=2,EF=![]() BC=
BC=![]() ,∴
,∴ ![]() ,∴ ∠DFE=90°,即异面直线PA与BC所成的角为90°.
,∴ ∠DFE=90°,即异面直线PA与BC所成的角为90°.
9.连结AM、DM.在△ABC和△DBC中,∵ AB=DB,AC=DC,BC=BC,∴△ABC≌△DBC,∴ AM=DM.在等腰△AMD中,∵ N是AD中点,∴ MN⊥AD于N,连结BN、CN,同理可证BN=CN,于是MN⊥BC于M,故MN是直线AD与BC的公垂线.
10.在△ABC中,∵ Q是AB中点,M是BC中点,∴
MQ∥AC,且MQ=![]() AC,同理PN∥AC,且PN=
AC,同理PN∥AC,且PN=![]() AC.∴
QM
AC.∴
QM![]() PN.∴
四边形MNPQ是平行四边形,又 ∵ PQ=
PN.∴
四边形MNPQ是平行四边形,又 ∵ PQ=![]() BD,QM=
BD,QM=![]() AC,AC=BD,∴
PQ=QM,∴
平行四边形MNPQ是菱形,∴
QN⊥PM.
AC,AC=BD,∴
PQ=QM,∴
平行四边形MNPQ是菱形,∴
QN⊥PM.
11.连结![]() 交
交![]() 于
于![]() ,连结BD交AC于O,连结
,连结BD交AC于O,连结![]() ,在矩形
,在矩形![]() 中,
中,![]() 是
是![]() 中点,O是AC中点,则
中点,O是AC中点,则![]() 于O.同理
于O.同理![]() 于
于![]() ,∴
,∴ ![]() 是异面直线AC和
是异面直线AC和![]() 的公垂线.∵
的公垂线.∵ ![]() =
=![]() =a,∴
AC与
=a,∴
AC与![]() 间的距离为a.
间的距离为a.
12.(1)∵ ![]() ∥
∥![]() ∥
∥![]() ,
,![]() =
=![]() =
=![]() ,∴
,∴ ![]() 是平行四边形,∴AC∥
是平行四边形,∴AC∥![]() ,又MN∥AC,因此,MN∥
,又MN∥AC,因此,MN∥![]() .
.
(2)由(1),![]() 是异面直线MN与
是异面直线MN与![]() 所成角.在△
所成角.在△![]() 中,
中,![]() ,
,![]() .于是有
.于是有![]() .
.
拓展练习
1.(1)由三角形中位线定理可知EF![]()
![]() AC,HG
AC,HG![]()
![]() AC,于是EF
AC,于是EF![]() HG,故四边形EFGH为平行四边形;
HG,故四边形EFGH为平行四边形;
(2)当AC=BD时,由EF=![]() AC,EH=
AC,EH=![]() BD,得EF=EH,即平行四边形EFGH的邻边相等,故平行四边形EFGH为菱形;
BD,得EF=EH,即平行四边形EFGH的邻边相等,故平行四边形EFGH为菱形;
(3)要使平行四边形EFGH为矩形,需且只须一个角是直角.如需EF⊥FG,则AC⊥BD;
(4)要使平行四边形EFGH为正方形,需且只须AC⊥ BD,且AC=BD;
2.(1)在一个平面内,过直线外一点有且只有一条直线与已知直线平行;在空间也如此.
(2)在一个平面内,过一点(该点可在直线上,也可在直线外)有且只有一条直线与已知直线垂线;在空间过直线上或直线外一点都有无数条直线和已知直线垂直,这无数条直线在过已知点的一个平面上(以后可知该平面与直线垂直).
(3)在一个平面内,与已知直线成60°角的直线有无数条,这无数条直线平行,且都与已知直线相交;在空间也是有无数条直线与已知直线成60°角,它们与已知直线位置关系是相交或异面.
3.(1)用反证法.假设EF与PC共面于a,则直线PE、CF共面a,则A∈a,B∈a,于是P与A、B、C共面于a,这与已知“P是平面ABC外一点”矛盾.故EF与PC是异面直线.
(2)取PB中点G,连结EG、FG,由E、F分别是线段PA、BC中点,有EG![]()
![]() AB,GF
AB,GF![]()
![]() PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
PC
∴ ∠GFE为异面直线EF与PC所成的角,∠EGF是异面直线PC与AB所成的角,∵ PC⊥AB,∴
EG ⊥GF,即∠EGF=90°.∵
PC=AB=2,∴ EG=1,GF=1,故△EFG是等腰直角三角形,∴ ∠GFE=45°,即EF与PC所成的角是45°.
(3)由(2)知Rt△EGF中EG=1,GF=1,∠EGF=90°,∴ EF=![]() .
.
4.(1)∵ ![]() ∥AC,∴
∥AC,∴
![]() 与AC所成的锐角或直角就是
与AC所成的锐角或直角就是![]() 与
与![]() 所成的角,连结
所成的角,连结![]() 、
、![]() ,在△
,在△![]() 和△
和△![]() ,∵
,∵ ![]() =
=![]() ,
,![]() ,
,![]()
![]()
![]() ,∴△
,∴△![]() ≌△
≌△![]() ,∴
,∴![]() .∴△
.∴△![]() 是等腰三角形.∵ O是底边AC的中点,∴
是等腰三角形.∵ O是底边AC的中点,∴
![]() ,故
,故![]() 与
与![]() 所成的角是90°.
所成的角是90°.
(2)∵
E、F分别是AB、AD中点,∴
EF∥BD,又∵
![]() ∥AC,∴
AC与BD所成的锐角或直角就是EF与
∥AC,∴
AC与BD所成的锐角或直角就是EF与![]() 所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与
所成的角.∵ 四边形ABCD是正方形,∴
AC⊥BD,∴
EF与![]() 所成的角为90°.
所成的角为90°.
(3)∵
EF∥BD,∴
![]() 为异面直线EF与
为异面直线EF与![]() 所成的角.∵ 四边形
所成的角.∵ 四边形![]() 是正方形,∴
是正方形,∴ ![]() ,∴ 在Rt△
,∴ 在Rt△![]() 中,
中,![]() ,
,![]() =
=![]() =
=![]()
![]() ,∴
,∴ 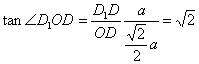 ,即EF与
,即EF与![]() 所成角的正切值为
所成角的正切值为![]() .
.
(4)∵
EF∥BD,BD⊥AC,∴
EF⊥AC,设交点为G.∵ ![]() ⊥AC(由(1)知)于O,则AC是异面直线EF与
⊥AC(由(1)知)于O,则AC是异面直线EF与![]() 的公垂线,OG的长即为EF与
的公垂线,OG的长即为EF与![]() 间的距离,由于G是OA中点,O是AC中点,且
间的距离,由于G是OA中点,O是AC中点,且![]() ,∴
,∴ ![]() ,即EF与
,即EF与![]() 间的距离为
间的距离为![]() .
.
5.②.①的逆命题为:空间四点中若任何三点都不共线,则这四点不共面.此命题是假命题.平行四边形的四个顶点是其反例.
②的逆命题为:若两条直线是异面直线,则这两条直线没有公共点,可知此命题为真命题.