空间直线与直线的位置关系

高二数学单元目标检测题

空间直线与直线的位置关系

班级　　　　　 学号　　　　　  姓名　　　　　　　　　  成绩　　　　　　 

一、选择题：（每小题3分，共36分）

  1.两条异面直线指的是　　　　　　　  （　）

A.没有公共点的两条直线　

B.分别位于两个不同平面内的两条直线

C.某一平面内的一条直线和这个平面外的一条直线

D.不同在任何一个平面内的两条直线

　 2.分别与两条异面直线都相交的直线　　  （　 ）

A.不可能是平行直线　　B. 一定是异面直线

C.不可能是相交直线　　　D.可能是平行直线

3.在空间四边形ABCD的边AB、BC、CD、DA上分别取点E、F、G、H，若EF与HG相交于一点M，则M　　　　　　　　　　 （　）

A.一定在直线AC上　 B.一定在直线BD上

C.可能在直线AC上,也可能在直线BD上　 D. 不在直线AC上，也不在直线BD上

4.关于异面直线的公垂线，下列说法正确的是　（　　 ）

A.垂直于两条异面直线的直线叫这面条异面直线的公垂线

B.在一条直线上取一点作与另一条垂直相交的直线叫这两条异面直线的公垂线

C.和两条异面直线都垂直相交的直线叫这两条异直线的公垂线

D.两条异面直线的公垂线有无数条

5.正方体ABCD-A₁B₁C₁D₁中，与A₁B所成的角为的棱有　　（　）

A.２条　　　B.４条　　C.６条　　D.８条

６.已知E、F、G、H是空间四点，设命题甲:点E、F、G、H不共面;命题乙:直线EF与GH不相交,那么甲是乙的　(　　)

A.充分不必要条件　 B. 必要不充分条件　C. 充要条件　D. 非充分非必要条件

7.已知a、b是异面直线,，则直线 c　　(　　　　　  )

A.必与a、b都相交　　　 B.至多与a、b中的一条平行

C.至多与a、b中的一条相交　　 D.至少与a、b中的一条平行

8.AB、CD、EF是两两异面垂直的直线,BC是AB、CD的公垂线,DE是CD、EF的公垂线,FA是EF、AB的公垂线,BC=3，DE=4,FA=5.则线段AD的长为　(　　)

A．　　B．　 C．　　D．

9.空间四边形ABCD的两对边AB=CD=3,E、F分别是AD、BC上的点,且AE:ED=BF:FC=1:2,EF=则AB与CD所成角大小为　　(　 )

A.　　　B. 　　 C.　　　　 D.

10.异面直线a、b所成角为,直线l与a、b所成的角都等于,则的取值范围是　 (　 )

A．　 B．　C．　 D．

11．对于已知直线a,如果直线b同时满足下列三个条件: (1)与a是异面直线　 (2)与a所成的角为定值　(3)与a的距离为定值,那么,这样的直线有　(　　)

N

A.1条　　 B.2条　　 C.3条　　 D.无数条

C

12 右图是正方体的平面展开图,在这个正方体中,

①　　

D

M

BM与ED平行,

②　　 CN与BE是异面直线,

③　　

B

E

A

CN与BM成角,

④ DM与BN垂直.

F

　以上四个个命题中，正确命题的序号是　　（　　）

　A.①②③　B.②④　　C.③④　　D.②③④

二、填空题：（每小题4分，共16分）

13.没有公共点的两条直线的位置关系是　　　　　　　　 

14.空间两个角和，若AB//A’B’，BC//B’C’, =则的大小是　　　　　　　

15.长方体ABCD-A₁B₁C₁D₁中，AB=4，AD=3，AA₁=2则A₁B₁与DD₁的距离为　　　　　　 

16.在正方体AC₁中，O、O₁分别是对角线BD和A₁D中点，E、F分别是棱

A₁B₁和B₁C₁中点，则异面直线EF和OO₁所成角的大小是　　　　　　　　

 

三、解答题：（共48分）

17.（8分）已知a、b是异面直线，直线c//a，且c不与b相交，求证：b、c是异面直线.

18.（10分）已知a、b是异面直线,点A、Ba,点C、Db,且AB=8,CD=6,AD、BC的中点分别是M、N,MN=5求证：ab

19.(10分)空间四边形ABCD中,AB=CD且AB与CD所成的角为,E 、F分别是

D

BC、AD的中点,求EF与AB所成的角的大小.

A

20.如图,已知ABCD与ABEF

B

是有公共边但不共面的矩形,它

们的面积和为25cm²,AD=2cm,

E

F

AF=3cm,的面积为cm²,求:

(1)　  AD与BE所成角的大小;

(2)AD与BE的距离.

21.(10分)空间四边形ABCD中,点M、N、P、Q分别在AB、BC、CD、DA上,且.

(1)　  求证: M、N、P、Q四点共面;

(2)　  当对角线AC=6,BD=3且MNPQ为正方形时,求AC与BD所成角的大小及k的值.

空间直线与直线的位置关参考答案

一、1 D 2 A 3 A 4 C 5 B 6 A 7 B　8 C  9 C 10 B 11 D　12　C

二、13 平行或异面　 14 或　15　3　　16　

三

17.证明：若b、c共面

∵b与c不相交　 ∴b//c　∵c//a　∴a//b这与a、b异面矛盾

∴b、c是异面直线

A

18. 证明：作BC的中点E，连结ME,NE

B

　　　　∵ME是的中位线

N

M

∴ME//AB,ME=AB=4

D

E

同理：EN//CD,EN=CD=3

　　　　 又∵MN=5

C

　　　　∴MN²=ME²+EN²

　　　　∴EM⊥EN

　　　　 ∵ME//AB,EN//CD

　　　　∴a与b所成的角就是ME与EN所成的角

　　　　∴a⊥b

 19 解:作BD的中点G,连结GF、GE

∵GF、GE分别是、的中位线

A

∴GF//AB,GF=AB;GE//CD,GE=CD

∴GF=GE

F

AB与CD所成的角就是GF与GE所成的角，

D

G

∵AB与CD所成的角为

B

∴或

C

E

∴或

又由AB//GF知EF与AB所成的角就是GF与EF所成的角，即为或

20　　　　　 解：（1）∵

∴

∴

∴或

∵AF//BE　∴AD与BE所成的角就是AD与AF所成的角即为

（2）∵AD⊥AB,AB⊥BE,AD∩AB=A,BE∩AB=B

∴AB是AD与BE的公垂线

∵2AB+3AB=25　∴AB=5cm

A

∴AD与BE的距离是5cm

21　　　　　

M

Q

(1)证明：∵

D

∴QM//BD，NP//BD　∴QM//PN

∴M、N、P、Q四点共面

P

N

B

（2）∵　∴PQ//AC

C

∵MQ//BD

∴AC与BD所成的角就是MQ与PQ所成的角

∵MQ⊥PQ

∴AC与BD所成的角为

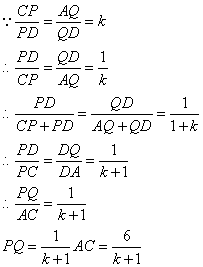
同理得：

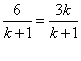∵PQ=MQ　∴　∴k=2