高二数学竞赛试题
一、选择题:本大题共10小题,每小题6分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、满足条件![]() 的集合
的集合![]() 的个数是
的个数是
(A)1个 (B)2个 (C)3个 (D)4个
![]() 2、在直角三角形中两锐角为A和B,则sinAsinB
2、在直角三角形中两锐角为A和B,则sinAsinB
(A)有最大值![]() 和最小值0 (B)既无最大值也无最小值
和最小值0 (B)既无最大值也无最小值
(C)有最大值![]() ,但无最小值 (D)有最大值1,但无最小值
,但无最小值 (D)有最大值1,但无最小值
3、已知![]() ,则下列不等式一定成立的是
,则下列不等式一定成立的是
(A)a2>b2 (B)ln a>ln
b (C)![]() (D)
(D)![]() >
>![]()
4设![]() 、
、![]() 是两个非零向量,则(
是两个非零向量,则(![]() +
+![]() )2=(
)2=(![]() )2+(
)2+(![]() )2是
)2是![]() ⊥
⊥![]() 的
的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
5、已知数列{![]() }的通项公式为an=2n-5,则a1+a2+…+a10=
}的通项公式为an=2n-5,则a1+a2+…+a10=
(A)68 (B)65 (C)60 (D)56
6、方程![]() =
=![]() 的解集是
的解集是
(A)(-1,0)∪(3,+∞) (B)(-1,0![]() ∪[3,+∞
∪[3,+∞![]()
(C)(-∞,-1)∪(0,3) (D)(-∞,-1)∪[0,3]
7、已知直线l1,l2关于直线y=x对称,且l1:y=ax+b(ab≠0),则l2的方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
8、已知cos(α-β)=![]() ,sinβ=-
,sinβ=-![]() ,且α∈(0,
,且α∈(0,![]() ),β∈(-
),β∈(-![]() ,0),则sinα=
,0),则sinα=
(A)![]() (B)
(B)![]() (C)-
(C)-![]() (D)-
(D)-![]()
9、已知x、y满足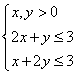 ,则z=x+y的最大值为
,则z=x+y的最大值为
(A)![]() (B)4
(C)1
(D)2
(B)4
(C)1
(D)2
10、计算机是将信息转换成二进制进行处理的,二进制即“逢2进![]() )2转换成十进制形式是
)2转换成十进制形式是
(A)217-2 (B)216-2 (C)216-1 (D)215-1
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
11、等比数列{![]() }中,a4+a6=3,则a5(a3+
}中,a4+a6=3,则a5(a3+
12、设函数f(x)=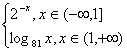 ,则满足f(x)≥
,则满足f(x)≥![]() 的x的取值范围为 .
的x的取值范围为 .
13、椭圆![]() 的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么PF1-PF2=
.
的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么PF1-PF2=
.
14、已知两个圆:x2+y2=1 ①;x2+(y-3)2=1 ②,则由①式减去②式可得上述两个圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为 .
高二数学竞赛试题
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 |
二、填空题
11、 ; 12、 ; 13、 ;
14、
.
三、解答题:本大题共6小题共74分.解答应写出文字说明.证明过程或演算步骤.
15、(本小题满分12分)
解关于x的不等式:![]() .
.
16、(本小题满分12分)
已知向量![]() =(
=(![]() x,x-4),向量
x,x-4),向量![]() =(x,
=(x,![]() x),x∈[-4,5]
x),x∈[-4,5]
(Ⅰ)试用x表示![]() ·
·![]() ;
;
(Ⅱ)求![]() ·
·![]() 的最大值,并求此时的cos<
的最大值,并求此时的cos<![]() 、
、![]() >.
>.
17、(本小题满分12分)
已知点![]() 到两个定点
到两个定点![]() 、
、![]() 距离的比为
距离的比为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程.
的方程.
18、(本小题满分12分)
某蛋糕厂生产某种蛋糕的成本为40元/个,出厂价为60元/个,日销售量为1000个,为适应市场需求,计划提高蛋糕档次,适度增加成本.若每个蛋糕成本增加的百分率为x (0<x<1),则每个蛋糕的出厂价相应提高的百分率为0.5x,同时预计日销售量增加的百分率为0.8x,已知日利润=(出厂价—成本)×日销售量,且设增加成本后的日利润为y.
(Ⅰ)写出y与x的关系式;
(Ⅱ)为使日利润有所增加,问x应在什么范围内?
19、(本小题满分12分)
已知f(x)=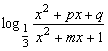 。是否存在实数p、q、m,使f(x)同时满足下列三个条件:①定义域为R的奇函数;②在[1,+∞
。是否存在实数p、q、m,使f(x)同时满足下列三个条件:①定义域为R的奇函数;②在[1,+∞![]() 上是减函数;③最小值是-1.若存在,求出p、q、m;若不存在,说明理由.
上是减函数;③最小值是-1.若存在,求出p、q、m;若不存在,说明理由.
20、(本小题满分14分)
已知某椭圆的焦点是![]() 、
、![]() ,过点F2并垂直到x轴的直线与椭圆的一个交点为B,且
,过点F2并垂直到x轴的直线与椭圆的一个交点为B,且![]() ,椭圆上不同的两点
,椭圆上不同的两点![]() 、
、![]() 满足条件:
满足条件:![]() 、
、![]() 、
、![]() 成等差数列。
成等差数列。
(Ⅰ)求该椭圆的方程;
(Ⅱ)求弦AC中点的横坐标;
(Ⅲ)设弦AC的垂直平分线的方程为![]() ,求m的取值范围。
,求m的取值范围。
高二数学竞赛试题
参 考 答 案
一、选择题
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答 案 | B | C | D | C | A | B | B | A | D | C |
二、填空题
11、9
12、![]() 13、3
13、3![]()
14、设圆方程(x-a)2+(y-b)2=r2 ① (x-c)2+(y-d)2=r2 ②(a≠c或b≠d),
由①-②,得两圆的对称轴方程.
三、解答题
15、![]()
![]()
![]() ,---------------------------------------------3分
,---------------------------------------------3分
当a=0时,原不等式![]()
![]()
![]() x<1,------------------------------------6分
x<1,------------------------------------6分
当a≠0时,原不等式![]()
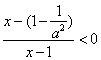
![]()
![]() .---------------11分
.---------------11分
综上可知,当a=0时,原不等式的解为![]() ;当a≠0时,原不等式的解为{x
;当a≠0时,原不等式的解为{x![]() }.-------------------------------------------------------------------12分
}.-------------------------------------------------------------------12分
16、(Ⅰ)![]() ·
·![]() =2x2-6x
-----------------------------------------------------------3分
=2x2-6x
-----------------------------------------------------------3分
(Ⅱ)设f(x)=2x2-6x=2(x-![]() )2-
)2-![]() ,
,
∵x∈[-4,5]
∴当x=-4时,![]() ·
·![]() 的最大值为56
--------------------------------------9分
的最大值为56
--------------------------------------9分
此时,![]() =(-2,-8),
=(-2,-8),![]() =(-4,-6),
=(-4,-6),![]() =
=![]() ,
,![]() =2
=2![]()
设![]() 、
、![]() 的夹角为θ,则cosθ=
的夹角为θ,则cosθ=![]() . ------------------12分
. ------------------12分
17、设点![]() 的坐标为
的坐标为![]() ,由题设有
,由题设有![]()
即![]()
整理得![]() ---------------------------------①--------------------4分
---------------------------------①--------------------4分
因为点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]()
所以∠![]()
![]() 450,直线
450,直线![]() 的斜率为±1
的斜率为±1
直线![]() 的方程为
的方程为![]() ---------------------------②--------------------8分
---------------------------②--------------------8分
将②式代入①式整理得![]()
解得![]()
代入②式得点![]() 的坐标为
的坐标为
(1,2)或(1,-2)--------------------------------------------------------------10分
故直线![]() 的方程为
的方程为![]() ----------------------------------------------------------12分
----------------------------------------------------------12分
18、(Ⅰ)由题意得
![]() ,
,
整理得 ![]() .------------------------------5分
.------------------------------5分
(Ⅱ)要保证日利润有所增加,当且仅当
![]() --------------------------------------------7分
--------------------------------------------7分
即 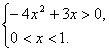 ----------------------------------------------------9分
----------------------------------------------------9分
解不等式得 ![]() .--------------------------------------------------------11分
.--------------------------------------------------------11分
答:为保证日利润有所增加,投入成本增加的比例![]() 应满足
应满足![]() .
.
-----------------------------------------------------------------------12分
19、∵f(x)是奇函数 ∴f(0)=0 得q=1 -------------------------------------1分
又f(-x)=-f(x) ∴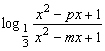 =-
=-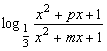
![]() =
=![]() 即(x2+1)2-p2x2=(x2+1)2-m2x2
即(x2+1)2-p2x2=(x2+1)2-m2x2
∴p2=m2
若p=m,则f(x)=0,不合题意。故p=-m≠0
∴f(x)=![]() -----------------------------------------------------5分
-----------------------------------------------------5分
由f(x)在[1,+∞![]() 上是减函数,令g(x)=
上是减函数,令g(x)=![]() =1-
=1-![]() =1-
=1-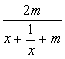
∵![]() 在[1,+∞
在[1,+∞![]() 上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞
上递增,在(-∞,-1)也递增,只有m>0时,在[1,+∞![]() 上g(x)递增,从而f(x)递减.--------------------------------------------------------7分
上g(x)递增,从而f(x)递减.--------------------------------------------------------7分
∴x=-1时,![]() 在(-∞,-1
在(-∞,-1![]() 上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.
上取得最大值-2,此时由f(x)的最小值为-1得g(x)的最大值为3.
1-![]() =3 得m=1, --------------------------------------------------------10分
=3 得m=1, --------------------------------------------------------10分
从而p=-1
综上可知,存在p=-1,q=1,m=1. ------------------------------------------------12分
20、(Ⅰ)∵椭圆的焦点是![]() 、
、![]() ,又点B在椭圆上,且
,又点B在椭圆上,且![]() ,
,
∴
故所求椭圆方程为![]() =1;-----------------------------------------------------4分
=1;-----------------------------------------------------4分
(Ⅱ)由于![]() 在椭圆上,则
在椭圆上,则![]() ,即
,即![]() ,
,
∴ ![]() =
=![]() =
=![]() =
=![]()
=![]() =
=![]() =
=![]() (∵-5≤
(∵-5≤![]() ≤5)
≤5)
同理 ![]() =
=![]() =
=![]() ,
,![]() =
=![]()
∵ ![]() 、
、![]() 、
、![]() 成等差数列,
成等差数列,
∴ 2![]() =
=![]() +
+![]() ,
,
即 ![]() =(
=(![]() )+(
)+(![]() )
)
∴ ![]() +
+![]() =8,
=8,
故弦AC中点的横坐标为4;--------------------------------------------------------8分
(Ⅲ)∵ 点A、C都在椭圆![]() =1上,
=1上,
∴ ![]() ,
,![]() ,
,
两式相减并整理得,![]() ,
,
由于弦AC的垂直平分线的方程为![]() ,
,
∴ ![]() ,又
,又![]() +
+![]() =8,
=8,
∴ ![]() =
=![]() ,
,
即AC中点坐标为M(4,![]() ),点M在直线
),点M在直线![]() 上,
上,
∴ k=-![]() ,
,
又点M在椭圆内,因此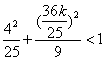 ,
,
则![]() ,即(-
,即(-![]() )2<
)2<![]() ,即
,即![]() ,
,
故m的取值范围为(—![]() ,
,![]() ).------------------------------------------14分
).------------------------------------------14分