高二数学空间向量测试题

高二数学空间向量测试题

班级___________ 姓名___________ 学号___________ 分数___________

一、选择题（共 10 小题）

1、已知直线a平行于平面α，且它们的距离为d，则到直线a与到平面α的距离都等于d的点的集合是（　）。

　 （A）空集　（B）二条平行直线　（C）一条直线（D）一个平面

2、若a, b是异面直线，且a//平面α，那么b与α的位置关系是（　）。

　 （A）b//α　（B）b与α相交　（C）b在α内　（D）不能确定

3、下列命题中正确的是（　）。

　 （A）若平面M外的两条直线在平面M内的射影为一条直线及此直线外的一个点，则这两条直线互为异面直线

　 （B）若平面M外的两条直线在平面M内的射影为两条平行直线，则这两条直线相交

　 （C）若平面M外的两条直线在平面M内的射影为两条平行直线，则这两条直线平行

　 （D）若平面M外的两条直线在平面M内的射影为两条互相垂直的直线，则这两条直线垂直

4、若a, b是异面直线，且a//平面α，那么b与α的位置关系是（　）。

　 （A）b//α　（B）b与α相交　（C）b在α内　（D）不能确定

5、三棱锥P－ABC的三条侧棱长相等，则顶点在底面上的射影是底面三角形的(　　)
A.内心　　　　　 B.外心　　　　　 C.垂心　　　　　　 D.重心

6、从平面α外一点P引直线与α相交，使P点与交点的距离等于1，这样的直线（　）。

　 （A）仅可作两条　　　　　　　　 （B）可作无数条

　 （C）可作一条或无数条和不能作　 （D）仅可作1条

7、若P是等边三角形ABC所在平面外一点，PA＝PB＝PC＝，△ABC的边长为1，则PC和平面ABC所成的角是（　）。

　 （A）30°　（B）45°　（C）60°　（D）90°

8、直线l与平面α内的两条直线垂直，那么l与α的位置关系是（  ）。

　 （A）平行　（B）lα  （C）垂直　（D）不能确定

9、三棱锥P－ABC的三条侧棱与底面所成的角相等，则顶点在底面上的射影是底面三角形的(　　)
A.内心　　　　　  B.外心　　　　　　  C.垂心　　　　　　  D.重心

10、棱台的上、下底面面积分别为4和9，则这个棱台的高与截得该棱台的棱锥的高之比为(　　)
A.1∶2　　　　　  B.1∶3　　　　　　  C.2∶3　　　　　　  D.3∶4

二、填空题（共 5 小题）

1、已知△ABC，点P是平面ABC外的一点，点O是点P在平面ABC上的射影，若点P到△ABC的三个顶点的距离相等，那么点O一定是△ABC的　　　　　　　  。

2、已知向量a＝(3,－2,6),b＝(－2,1,0),则
2a＝____(6,－4,12)_______
－b＝____(－1,,0)____
2a＋3b＝_____(0,－1,12)_____
a－b＝_____(3,－,2)____
a²＝______49_____
b²＝______5______
a·b＝______－8______
(3a＋2b)(a－3b)＝______173_____
<a,b>＝______π－arccos______
a在b上的投影为____－ ______

3、设斜线和平面所成的角为θ，那么斜线和平面内过斜足的所有直线的夹角中，最大角为　　  　　　　　；最小角为　　　　　　  。

4、若直线l与平面α相交于点O，A、B∈l，C、D∈α，且AC//BD，则O、C、D三点的位置关系是　　　　　　　  。

5、过平面α外一点P的斜线段是过这点垂线段的倍，则斜线与平面α所成的角为　　　　　　　  。

三、计算题（共 2 小题）

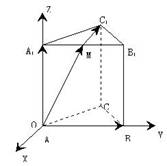
1、如图，正三棱柱ABC—A₁B₁C₁的底面边长为，侧棱长为a.
　(1).建立适当的坐标系，并写出点A、B、A₁、C₁的坐标；
　(2).求AC₁与侧面ABB₁A₁所成的角

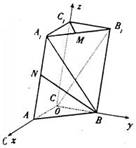2、如图，直三棱柱ABC－A₁B₁C₁底面ΔABC中，CA＝CB＝1，∠BCA＝90o，棱AA₁＝2，M、N分别是A₁B₁、A₁A的中点。
(1)求BN的长；
(2)求cos<>的值；
(3)求证：A₁B⊥C₁M。

四、证明题（共 2 小题）

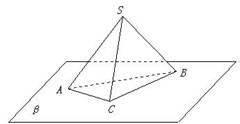1、P是△ABC所在平面外一点，PA⊥BC，PB⊥AC，求证：PC⊥AB.

2、两个全等的正方形ABCD和ABEF不在同一平面内，M、N分别在它们的对角线AC、BF上，且CM＝BN，求证：MN//平面BCE。

空间向量测试题 答案

一、选择题（共 10 小题）

1、B 2、D 3、A 4、D 5、B 6、C 7、A 8、D 9、B 10、B

二、填空题（共 5 小题）

1、外心 2、 3、;θ. 4、共线 5、60°

三、计算题（共 2 小题）

1、解：(1)如图，以点A为坐标原点O，以AB所在直线为Oy轴，以AA₁所在直线为Oz轴，以经过原点且与平面ABB₁A₁垂直的直线为Ox轴，建立空间直角坐标系。
由已知，得A(0,0,0),B(0,a,0),A₁(0,0,a)，
C₁(－
(2)建立坐标系如图。取A₁B₁的中点M，
于是有M(0,，连AM,MC₁有
a,0,0)，且
＝(0,a,0),
由于
所以，MC₁⊥面ABB₁A₁
∴AC₁与AM所成的角就是AG₁与侧面ABB₁A₁所成的角。
∵
∴
而

cos<
所以，所成的角，即AC₁与侧面ABB₁A₁所成的角为30o.

2、解：如图，以C为原点建立空间直角坐标系O－xyz

(1)解：依题意得B(0，1，0)，N(1，0，1)，
　　　∴
(2)解：依题意得A₁(1，0，2)，B(0，1，0)，C(0，0，0)，B₁(0，1，2)。
　　　 ∴ ＝(1，－1，2)，＝(0，1，2)。
　　　　＝3，
　　　∴ cos<
(3)证明：依题意得C₁(0，0，2)，M(，2)
　　 ＝(－1，1，－2)，，0)，
　∴ ＋0＝0，∴

四、证明题（共 2 小题）

1、证明略

2、证明略