高二数学期初测试
(满分:150分 考试时间:120分钟)
第Ⅰ卷(选择题 共60分)
一、选择题
1.已知直线![]() 与
与![]() 平行,则实数
平行,则实数![]() 的取值是
的取值是
A.-1或2 B.0或
2.已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上的任意一点,则
△ABC面积的最小值是
A. 6 B.3+![]() C.
C.![]() D.3-
D.3-![]()
3.已知点P是以![]() 、
、![]() 为焦点的椭圆
为焦点的椭圆![]() 上一点,
上一点,![]() ,则点P与坐标原点O的距离为
,则点P与坐标原点O的距离为
A.
5
B![]() D.
D.![]()
4.抛物线的顶点在坐标系原点,焦点是椭圆4x2+y2=1的一个焦点,则此抛物线的焦点到准线的距离为
A. ![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
5.设有不同的直线a、b和不同的平面α、β、γ,给出下列三个命题:
①若a∥α,b∥α,则a∥b; ②若a∥α,a∥β,则α∥β;
③若α⊥γ,β⊥γ,则α∥β.
其中正确的命题个数是
A.0 B
6.设△ABC和△DBC所在两平面互相垂直,且AB=BC=BD=a,∠CBA=∠CBD=120°,则AD与平面BCD所成的角为
A.30° B.45° C.60° D.75°
7.已知双曲线中心在原点且一个焦点F(![]() ,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,0),直线y=x-1与其相交于M、N两点,MN中点的横坐标为![]() ,则双曲线方程为
,则双曲线方程为
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
8. 设![]() 1是曲线y2=2px(p≠0)与ax2+by2=1(a>b>0)的离心率的比值,
1是曲线y2=2px(p≠0)与ax2+by2=1(a>b>0)的离心率的比值,![]() 2是曲线ax2-by2=1上一点到右准线和右焦点的距离之比,则
2是曲线ax2-by2=1上一点到右准线和右焦点的距离之比,则
A ![]() B
B ![]() C
C ![]() D 以上都不对
D 以上都不对
9.已知平面内有一条线段AB,其长度为4,动点P满足PA-PB=3,O为AB的中点,则PO的最小值为
A ![]() . B.
. B.
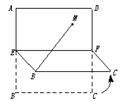
10.正方形ABCD边长为2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图),M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为![]() ,那么点M到直线EF的距离为
,那么点M到直线EF的距离为 
![]() 11.如果直线
11.如果直线![]() 与圆
与圆![]() 交于M、N两点,且M、N关于直线
交于M、N两点,且M、N关于直线![]() 对称,则不等式组
对称,则不等式组 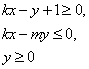 表示的平面区域的面积是
表示的平面区域的面积是
A.1 B.![]() C.2
D.
C.2
D.![]()
12.斜率为1的直线l与椭圆![]() +y2=1相交于A、B两点,则AB的最大值为
+y2=1相交于A、B两点,则AB的最大值为
A.2 B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题
13.直线l经过抛物线y2=4x的焦点,且与准线成60°角,则直线l的方程是 .(注:填上你认为正确的一个方程即可,不必考虑所有可能的情况)
14.已知a、b、c、d是四条互不重合的直线,且c、d分别为a、b在平面![]() 上的射影,给出下面两组四个论断:
上的射影,给出下面两组四个论断:
第一组:①a⊥b,②a∥b;
第二组:③c⊥d,④c∥d.
分别从两组中各选一个论断,使一个作条件,另一个作结论,写出一个正确的命题: .
15.以椭圆![]() +
+![]() =1的中心O为顶点,以椭圆的左准线l1为准线的抛物线与椭圆的右准线l2交于A、B两点,则AB的值为 .
=1的中心O为顶点,以椭圆的左准线l1为准线的抛物线与椭圆的右准线l2交于A、B两点,则AB的值为 .
16.已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、60°,则以OC为棱的二面角A—OC—B的余弦值等于 .
三、解答题
17.(本小题满分12分)
已知x,y满足不等式组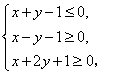 求
求![]() 的最大值和最小值。
的最大值和最小值。
18.(本小题满分12分)
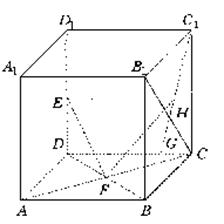
如图,在棱长为1的正方体ABCD—A1B1C1D1中,E、F分别是D1D、DB的中点,![]() 在棱CD上.
在棱CD上.![]() ,H是C1
,H是C1![]() 的中点.
的中点.
(Ⅰ)求证:EF⊥B1C;(Ⅱ)求EF与C1![]() 所成角的余弦值;(Ⅲ)求FH的长.
所成角的余弦值;(Ⅲ)求FH的长.
19.已知点F(1,0),直线![]() ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M。
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M。
(1)求点M的轨迹C的方程;
(2)设![]() 与x轴相交于H,直线BF与曲线C相交于P、Q两点,求证:直线HP、HQ与直线HF的夹角相等。
与x轴相交于H,直线BF与曲线C相交于P、Q两点,求证:直线HP、HQ与直线HF的夹角相等。
20.(本小题满分12分)
已知双曲线的一个集点为![]() ,且渐近线为
,且渐近线为![]() 。过点A(2,1)的直线
。过点A(2,1)的直线![]() 与该双曲线交于
与该双曲线交于![]() 两点。
两点。
(Ⅰ)求线段![]() 的中点P的轨迹方程;
的中点P的轨迹方程;
(Ⅱ)过点B(1,1)能否作直线![]() ,,使
,,使![]() ,与已知双曲线交于两点
,与已知双曲线交于两点![]() ,且B是线段
,且B是线段![]() 的中点,请说明理由。
的中点,请说明理由。
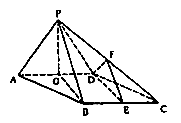
21.(本小题满分12分)如图,在立体图形P-ABCD中,底面ABCD是∠DAB=60°,且边长为a的菱形。侧面PAD为正三角形,其所在平面垂直于底面ABCD。
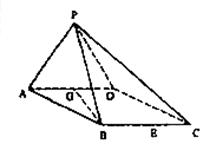
(Ⅰ)若G为AD边的中点,求证BG⊥平面PAD;(Ⅱ)求证AD⊥PB;
(Ⅲ)求二面角A-BC-P的在小;
(Ⅳ)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF⊥平面ABCD,并证明你的结论。
22.(本小题满分14分)
如图所示,在Rt△ABC中,∠CAB=90°, AB=2, AC=![]() , D是线段AB的垂直平分线上的一点, D 到AB的距离为2, 过点C的曲线E上任一点P满足
, D是线段AB的垂直平分线上的一点, D 到AB的距离为2, 过点C的曲线E上任一点P满足![]() 为常数.
为常数.
①建立适当的坐标系,并求出曲线E的方程.
②过点P的直线 l与曲线E相交于不同的两点M , N , 且M点在D, N 之间,若![]() , 求
, 求![]() 的取值范围.
的取值范围.
|
高二数学期末测试参考答案
一、选择题:5×12=60分
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | B | D | A | B | C | C | A | C | D | C |
二、填空题:4×4=16分
13、![]() 14、若a∥b,则c∥d 15、
14、若a∥b,则c∥d 15、![]() 16、
16、![]()
三、解答题:共74分
17. (本题满分12分)如图不等组为不等式所表示的可行域
令u=x-2y
作出![]()
在可行域内平行移动![]() 得
得![]() ,可知A、B为满足条件的最优解。
,可知A、B为满足条件的最优解。
由![]() 得A(1,0),
得A(1,0),![]()
由![]()
得B(3,-2),![]()
∴![]() 。
。
18.(本题满分12分)
(Ⅰ)证明:选取DA1、DC、DD1,分别为Ox、Oy、Oy轴建立空间直角坐标,易知E(0,0,![]() ),F(
),F(![]() ,
,![]() ,0),B1(1,1,1),C(0,1,0),
,0),B1(1,1,1),C(0,1,0),
![]() ,
,
![]()
=0,
![]() .
.
(Ⅱ)解:G(0,![]() ,-1),Cl(0,1,1),
,-1),Cl(0,1,1),
![]()
![]() .
.
(Ⅲ)解:![]() ,
,
![]()
![]()
![]()
19解:(1)由已知易得MF=MB由抛物线定义得点M的轨迹方程为
![]() (
(![]() ≥0)
≥0)
(2)设直线![]() 方程
方程![]() 设P
设P![]()
则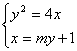 消去
消去![]() 得
得![]() ∴
∴![]()
而![]()
![]()
∴![]()
同理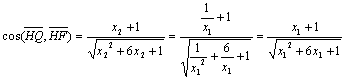
∵向量所成角范围在[0,![]() ]上 ∴结论成立。
]上 ∴结论成立。
20.(本题满分12分)
解:(Ⅰ)双曲线的方程为![]()
设![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,中点P(x,y)
,中点P(x,y)
则![]()
![]()
①②得,![]()
当![]() 时,
时,![]() ③
③
∵![]() 四点共线 ∴
四点共线 ∴![]() ④
④
由③、④得![]() ,即
,即![]()
当![]() 时,x=2,y=0满足此方程。
时,x=2,y=0满足此方程。
∴中点P的轨迹方程是 ![]()
(Ⅱ)假设存在直线L′同(1)可得L′的斜率为2,L′的方程为y=2x-1。
∵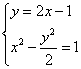 无解,与假设矛盾,∴满足条件的直线L′不存在。
无解,与假设矛盾,∴满足条件的直线L′不存在。
21.(本题满分12分)
(Ⅰ)证明 ∵在菱形ABCD中,∠DAB=60°,G为AD的中点,BG⊥AD,
又平面PAD⊥平面ABCD的,平面PAD∩平面ABCD=AD
∴BG⊥平面PAD。
(Ⅱ)证明 连结PG,因为△PAD为正三角形,G为AD的中点,得PG⊥AD。
由(Ⅰ)知BC⊥AD,PG∩BG=G,PG![]() BG=G,PG
BG=G,PG![]() 平面PGB,BG
平面PGB,BG![]() 平面PGB。
平面PGB。
∴AD⊥平面PGB。
∵PB![]() 平面PGB。
平面PGB。
∴AD⊥PB。
(Ⅲ)解 由(Ⅱ),AD⊥平面PGB,
∵在菱形ABCD中,AD∥BC,
∴BC⊥平面PGB。,
而PB![]() 平面PGB,BG
平面PGB,BG![]() 平面PGB
平面PGB
∴BC⊥PB,BC⊥BG。
∴∠PBG为二面角A-BC—P的平面角。
∵在△PAD中,![]() ,在菱形ABCD中,
,在菱形ABCD中,![]() ,
,
∴在Rt△PGB中,∠PGB=45°
∴二面角A-BC-P为45°。
(Ⅳ)当F为BC中点时,满足平面DEF⊥平面ABCD。
证明 取PC的中点F,连结DE,EF,DF,则由平面几何知识,
在△PBC中,FE∥PB,
在菱形ABCD中,GB∥DE,
而FE![]() 平面DEF,DE
平面DEF,DE![]() 平面DEF,FE∩DE=E,
平面DEF,FE∩DE=E,
∴平面DEF∥平面PGB。
由(Ⅰ),PG⊥平面ABCD,而PG![]() 平面PGB,
平面PGB,
∴平面PGB⊥平面ABCD。
∴平面DEF⊥平面ABCD。
22.(本题满分12分)
解:①以AB、OD所在直线分别为X轴、Y轴建立直角坐标系
![]() ∴动点的轨迹为以A、B为焦点的椭圆
∴动点的轨迹为以A、B为焦点的椭圆
![]()
②l与y轴重合,DM=1,DN=3,![]() ,
,
l不与y轴重合,D(0,2)令直线MN的方程为:y=kx+2与曲线C的方程联立得
![]()
△=![]()
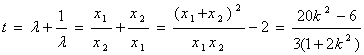
![]()