高二数学期末考试试题

高二数学期末考试试题　　

题号	一	二	三					总分
			21	22	23	24	25
得分

一、填空题：（3*10分）

1、，则　　　　  　

2、设为的单位向量，则的坐标为　　　 　  。

3、 已知F₁=， F₂ =，F₃= ,若F₁、F₂、F₃共同作用在物体上，使物体从点M₁(2,-3,2)移到M₂（4，2，3），则合力所作的功　　　　 　

4、已知点A(3,3)，B（-1，5），直线y=kx+1与线段AB有公共点，则实数k的取值范围为

　　　　　　　

5、直线斜率之积为-1是直线的　 　　　　 条件。

6、若P－ABCDEF为正六棱锥，则∠APB的取值范围为__　 _____。

7、过棱锥高作平行于底面的截面，将棱锥的体积分成上、下相等的两部分，则侧棱被分成上、下两段之比为__ 　______　。

8、已知斜棱柱直截面周长为8，高为4，侧棱与底面成60°角，则斜棱柱侧面积是_________。

9、四面体的一条棱长是x,其余棱长都是1，则该四面体的体积最大时，x的值为　 　　　  。

10、棱长为a的正方体中，连结相邻面的中心，以这些线段为棱的八面体的体积为　　   。

二、选择题：（3*10分）

题号	11	12	13	14	15	16	17	18	19	20
答案

11、经过点（-5，-1），在两坐标轴上截距相等的直线有（　　）

（A）、0条　　　　 （B）、 1条　　 （C）、 2条　　　（D）、3条

12、下列命题中正确的是（　 ）

（A）、　 （B）、若则

（C）、　　　　　 （D）、若是平行向量且则

13、若若平行，则实数a为（　　 ）

（A）、4　　（B）、　　（C）、　　  （D）、0

14、边长为2的等边三角形ABC中，设，

则等于（　　 ）

（A）、0 　 （B）、-3 　 （C）、-6　　  （D）、3

15、在下列条件中，可判断平面α与β平行的是（　　）

　　　　　　　　　　　　　　　　　　　 A．α、β都垂直于平面r.

　　　　　　　　　　　　　　　　　　　 B．α内存在不共线的三点到β的距离相等.

　　　　　　　　　　　　　　　　　　　 C．l，m是α内两条直线，且l∥β，m∥β.

　　　　　　　　　　　　　　　　　　　 D．l，m是两条异面直线，且l∥α，m∥α, l∥β，m∥β.

16、下列四个命题中，其本身与其逆命题都成立的是（　　 ）

A．正四棱柱一定是长方体　　　　　 B．正方体一定是正四棱柱

C．直平行六面体一定是直四棱柱　　 D．侧棱与底面垂直的棱柱是直棱柱

17、一个四棱锥的所有侧面与底面所成的角都是30°，若此棱锥的底面面积为S，则它的侧面面积等于（　　 ）

A．　　　 B．　　　　　 C．　 D．2S

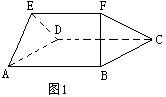
18、如图1，在多面ABCDEF中，已知面ABCD是边长为3的正方形，EF∥AB，，EF与面AC的距离为2，则该多面体的体积为（　　　　　 ）

（A）　　　　（B）5　　　　　（C）6　　　　　　　　 （D）

19、正三棱锥S－ABC的底面边长为a，侧棱长为b，M为AC的中点，N为BC的中点，过MN平行于SC的平面在正三棱锥内的截面面积为（　　  ）

A．　　　 B．　　　　C．　　　 D．

20、已知α，β是平面，m，n是直线.下列命题中不正确的是　　　　（　　）

　　　A．若m∥n，m⊥α，则n⊥α　　　　　　　 B．若m∥α，α∩β=n，则m∥n

　　　 C．若m⊥α，m⊥β，则α∥β　　　　　　 D．若m⊥α，，则α⊥β

三、解答题：

21、（本题6分）

已知与的夹角为

（1）求

（2）若，问实数m为何值时，？

22、（本题6分）

已知三棱锥O-ABC中，OA、OB、OC两两垂直，且OA=x，OB=y，OC=1,又x+y=4,问当x、y为何值时这棱锥的体积最大？最大值是多少？

23、（本题8分）

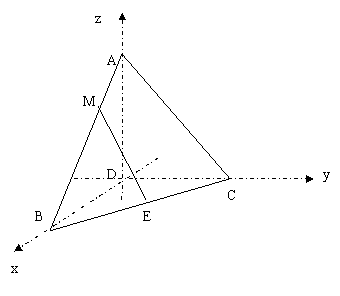
如图，三棱锥A-BCD中，底面BCD，且AD=BD=DC=1，设E为BC的中点，M在AB上且满足，如图建立空间直角坐标系

（1）写出点M、E的坐标，并求异面直线ME与DC所成角的大小

（2）在侧棱AC上是否存在一点P，使？若存在，求出点P的坐标；若不存在，请说明理由。

24、（本题10分）

已知正四棱柱ABCD—A₁B₁C₁D₁，AB=1，AA₁=2，点E为CC₁中点，点F为BD₁中点.

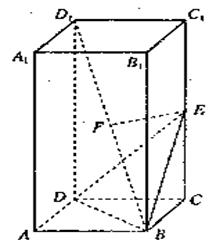
　 （1）证明EF为BD₁与CC₁都垂直；

　 （2）求点D₁到面BDE的距离.

25、（本题10分）

 如图，正三棱柱ABC—A₁B₁C₁的底面边长的3，侧棱AA₁=D是CB延长线上一点，且BD=BC.

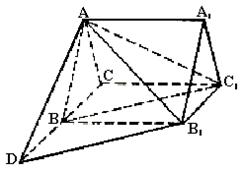
　 （Ⅰ）求证：直线BC₁//平面AB₁D；

　 （Ⅱ）求二面角B₁—AD—B的大小；

　 （Ⅲ）求三棱锥C₁—ABB₁的体积.

2003闵行三中高二期末考试题答案　　 2004-1-8

一、填空题：（3*10分）

1、　  2、 　 3、16　 　　 4、 　　5、充分不必要

6、（0,）　7、　 8、 　 9、　　　　　　　　　10、

二、选择题：（3*10分）

题号	11	12	13	14	15	16	17	18	19	20
答案	D	C	C	C	D	D	C	D	A	B

三、解答题：

21、（1）　　  ……3分

　 （2）　　　 ……3分

22、因为：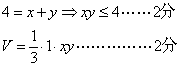　　　　　　 

　　 所以

23、 （1）、

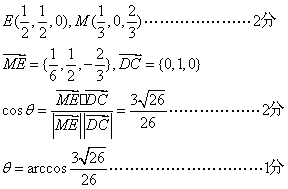
　 （2）、令P（0，b,1-b）　满足题设。　　

24、（1）以D为坐标原点建立空间直角坐标系 　　　　　　　　　　

　　　　　　　 

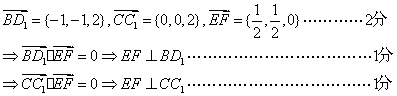
（2）解：设点D₁到面BDE的距离为d，连结ED₁，

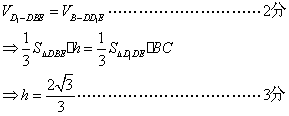
25、（1）证明：CD//C₁B₁，又BD=BC=B₁C₁， ∴ 四边形BDB₁C₁是平行四边形，

∴BC₁//DB₁.又DB₁平面AB₁D，BC₁平面AB₁D，∴直线BC₁//平面AB₁D.

（2）解：过B作BE⊥AD于E，连结EB₁，

∵B₁B⊥平面ABD，∴B₁E⊥AD ，

∴∠B₁EB是二面角B₁—AD—B的平面角，

∵BD=BC=AB，

∴E是AD的中点，

在Rt△B₁BE中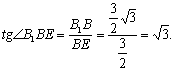，∴∠B₁EB=60°

（3）解法一：过A作AF⊥BC于F，∵B₁B⊥平面ABC，∴平面ABC⊥平面BB₁C₁C，

∴AF⊥平面BB₁C₁C，且AF=

 即三棱锥C₁—ABB₁的体积为　　

　　　　解法二：在三棱柱ABC—A₁B₁C₁中，

　即三棱锥C₁—ABB₁的体积为