高二数学期末试卷
一.选择题:(5![]() 12)
12)
1.
A={xx2-2![]() 0}, B={xx2-4x+3
0}, B={xx2-4x+3![]() 0},则A
0},则A![]() B=
( C )
B=
( C )
(A){xx![]()
![]() 或x
或x ![]() 1} (B){xx
1} (B){xx![]()
![]() 或x
或x![]() 3}
3}
(C)![]() {xx
{xx ![]() -
-![]() 或x
或x![]() 1} (D) R
1} (D) R
2 .a=1是直线x+ay=a+2与直线ax+y=
(A) 充要条件 (B) 充分不必要条件
(C) 必要不充分条件(D)既不充分也不必要条件
3. 奇函数y=f(x)在x ![]() (0, +
(0, +![]() )时,f(x)=x-1,则f(x-1)<0的解集为 ( B )
)时,f(x)=x-1,则f(x-1)<0的解集为 ( B )
(A){x-1<x<0} (B){xx<0,或1<x<2}
(C){x0<x<2} (D){x1<x<2}
4. 过抛物线y2=4x的焦点作直线交抛物线于A(x1 , ,y1)B(x2, ,y2)两点,
若AB与x轴成45![]() ,则AB的长为
( B )
,则AB的长为
( B )
(A)10 ( B) 8 ( C) 6 ( D) 4
5 .定义在R上的偶函数f(x)满足f(x+4)= -f(x),在[0,4]上
为减函数 ,则 ( B )
(A)f(10)<f(13)<f(15), (B)f(13)<f(10)<f(15)
(C)f(15)<f(10)<f(13) (D)f(15)<f(13)<f(10)
6 .设椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,F,A分别是椭圆的左焦点,右顶点,B是它短轴的一个端点,则
,F,A分别是椭圆的左焦点,右顶点,B是它短轴的一个端点,则![]() ABF 为
( C )
ABF 为
( C )
(A) 30 ° (B) 75° (C)90° (D) 120°![]()
7.如果存在实数a,使cosa=![]() 成立,那么实数x的集合是 ( A )
成立,那么实数x的集合是 ( A )
(A){-1.1}(B){xx<0或x=1}(C) { xx>0或x=-1}(D){xx![]() -1 或x
-1 或x![]() 1}
1}
8.若抛物线y2=2px (p>0)上三点的纵坐标的平方成等差数列,那么
这三点的焦半径的关系为 ( A )
(A) 成等差数列 (B)成等比数列
(C) 既成等差数列又成等比数列 (D)既不成等差数列又不成等比数列
9.已知双曲线![]() 的半焦距为c,顶点A(a,0)到渐近线
的半焦距为c,顶点A(a,0)到渐近线
的距离为![]() c,则双曲线的离心率为
( B )
c,则双曲线的离心率为
( B )
(A)![]() (B)
(B)![]() (C)
(C)![]() ,
,![]() (D)
(D)![]()
10.已知函数f(x)=x ![]() G(x)(x
G(x)(x![]() R)在区间(-
R)在区间(-![]() ,0)上为减函数,又G(x)为奇函数,
,0)上为减函数,又G(x)为奇函数,
则对任意实数,下列不等式成立的是 ( A )
(A) f(a2±a+1) ![]() f(-
f(-![]() ) (B) f(a2+a+1) >f(-
) (B) f(a2+a+1) >f(-![]() )
)
(C) f(a2±a+1) ![]() f(-
f(-![]() ) (D) f(a2+a+1) <f(-
) (D) f(a2+a+1) <f(-![]() )
)
11按向量a平移将x2+y2+4x+2y+1=0化简为标准方程
,则向量a的坐标为 ( D )
(A)(-2,1) (B)(2,-1)(C)(-2,-1)(D)(2,1)
12.设F1,,F2为椭圆的两焦点,M是椭圆上的任一点,从任一焦点向
![]() F1MF2的顶点M的外角平分线作垂线,垂足为P,
F1MF2的顶点M的外角平分线作垂线,垂足为P,
则P点的轨迹为 ( A )
(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
二.填空题 (每题4分 )
13.若x,y 满足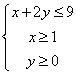 则2x+y的最大值为 18
则2x+y的最大值为 18
14.设F1,,F2为双曲线![]() 的两焦点 ,点P在双曲线上,且
的两焦点 ,点P在双曲线上,且![]() F1PF2 =60
F1PF2 =60![]() ,则
,则![]() F1PF2 的面积为
F1PF2 的面积为
![]()
15.已知不等式2x-t+t-1<0的解集为(-![]() )则t为 0
)则t为 0
16.1.x+x-1>m的解集为R
2.函数f(x)= - (7
若这两个命题中有且仅有一个为真命题,则实数m的范围为 1![]() m<2
m<2![]()
三.解答题:(12+12+12+12+12+14)
17
已知函数f(x)=lg![]() ,
,
(1) 求函数f(x)的定义域
(2)
当a= -1,x![]() (3,+
(3,+![]() )时, 求函数f(x)的值域
)时, 求函数f(x)的值域
(1)解:原函数的定义域等价于 (x-a)(x-1)>0
1.
当a=1 时,![]() ;
;
2. 当a>1时,x>a或x<1;
3. 当a<1时,x>1或x<a
所以原函数的定义域为
当a=1 时,{x![]() }
}
当a>1时,{xx>a或x<1};
当a<1时,{xx>1或x<a}
(2) 当a=-1 时,已知函数f(x)=lg![]() ,
,
x![]() (3,+
(3,+![]() )时,函数的值域为(0,lg2)
)时,函数的值域为(0,lg2)
![]()
![]()
![]() 19.设x1,x2
19.设x1,x2![]() R,常数a>0,定义运算“
R,常数a>0,定义运算“![]() ”:x1
”:x1 ![]() x2=(x1+x2)2
,定义运算“ ”:x1 x2=(x1-x2)2
x2=(x1+x2)2
,定义运算“ ”:x1 x2=(x1-x2)2
![]() (1)若
(1)若![]() ,求动点P(
,求动点P(![]() )的轨迹C的方程
)的轨迹C的方程
(2)已知直线L:y=![]() x+1与(1)中的轨迹交于A(x1,y1),B(x2,y2),若
x+1与(1)中的轨迹交于A(x1,y1),B(x2,y2),若
![]() =8
=8![]() ,试求a的值。
,试求a的值。
解:(1)y=4ax(y![]() 0)
4分
0)
4分
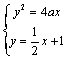 得x2+4(1
得x2+4(1![]() 8分
8分
AB![]() =
= ![]()
解得 a=2![]() 12分
12分
19.设圆C的圆心在直线x-y-1=0上,且与直线4x+3y+14=0相切,又圆C截直线3x+4y+10=0所得的弦长为6,求圆方程
因为圆心在直线x-y-1=0上,所以设圆C的圆心坐标为(a,a-1);
圆方程为(x-a)2+(y-a+1)2 = r 2
因为圆与直线4x+3y+14=0相切,所以![]() ;
;
又圆截直线3x+4y+10=0所得的弦长为6,所以![]()
解得a=2,r=5, 所以圆方程为(x-2)2+(y-1)2=25 12分
20.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,售量为1000辆,本年度为适应市场需求,计划提高产品档次,适度增加投入成本,若每辆车投入成本增加的比例为x(0<x<1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价-投入成本)年销量。
(1)写出本年度预计的年利润y与投入成本增加的比例x 关系式。
(2)为使本年度的年利润比上一年有所增加,问投入成本的比例x应在什么范围内?
(1)y=[1.2(1+0.75x)-1(1+x)](1+0.6x)![]() 1000
(0<x<1) 不写条件扣1分 6分
1000
(0<x<1) 不写条件扣1分 6分
(2)![]() 解得0<x<
解得0<x<![]()
答: (不答扣1分)
21.双曲线![]() (a,b>0),一焦点到其相应准线的距离为
(a,b>0),一焦点到其相应准线的距离为![]() ,过点A(0,-b)B(a,0)的直线与原点的距离为
,过点A(0,-b)B(a,0)的直线与原点的距离为![]()
(1) 求该双曲线的方程
(2)
是否存在直线y=kx+5(k![]() 0,)与双曲线交于相异两点C,D,使得 C,D两点都在以A为圆心的同一个圆上,若存在,求出直线方程 ;若不存在说明理由。
0,)与双曲线交于相异两点C,D,使得 C,D两点都在以A为圆心的同一个圆上,若存在,求出直线方程 ;若不存在说明理由。
解:因为焦点到其相应准线的距离为![]() ,所以
,所以![]() ; 又因为过点A(0,-b)B(a,0)的直线与原点的距离为
; 又因为过点A(0,-b)B(a,0)的直线与原点的距离为![]() ;可设直线方程为
;可设直线方程为![]() ,由点到直线的距离公式得
,由点到直线的距离公式得![]() ,解得a=
,解得a=![]() ,b=1,所以双曲线方程为
,b=1,所以双曲线方程为![]() 5分
5分
(3)
假设存在直线y=kx+5(k![]() 0,)与双曲线交于相异两点C,D,使得 C,D两点都在
0,)与双曲线交于相异两点C,D,使得 C,D两点都在
以A为圆心的同一个圆上
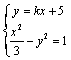 得(1-3k2)x2-30kx-78=0;可得
得(1-3k2)x2-30kx-78=0;可得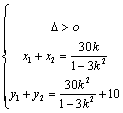
因为C,D两点都在以A为圆心的同一个圆上;所以有AC=AD,
所以直线CD的中点坐标为M![]() 因为AM
因为AM![]() CD,
CD,
所以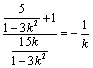 ,解得k=
,解得k=![]() ,所以直线方程为y=
,所以直线方程为y=![]() x+5
12
x+5
12
22.在直角坐标系中,三角形ABC的两个顶点C,A的坐标为(-![]() ,0),(
,0),(![]() ,0),
,0),
三内角A,B,C满足2sinB=![]() (sinA+sinC)
(sinA+sinC)
(1) 求顶点B的轨迹方程
(2)过顶点C作直线与顶点B的轨迹交于P,Q两点当倾斜角在(0,90°)时
求三角形APQ面积的最大值
设三角A、B、C 所对三边为a、b、c,由2sinB=![]() (sinA+sinC)得2b=a+c,
(sinA+sinC)得2b=a+c,
b=2![]() 得a+c=4即BC+CA=4,由椭圆的定义知B的轨迹为以C,A为焦点长轴长为 4,中心在原点的椭圆。
得a+c=4即BC+CA=4,由椭圆的定义知B的轨迹为以C,A为焦点长轴长为 4,中心在原点的椭圆。
所以椭圆的方程为![]() (y
(y![]() 0)
0)
(2)设直线方程为x=ky-![]() ,与椭圆方程联列得
,与椭圆方程联列得
(k2+4)y2-2![]() ky-1=0,所以y1+y2=
ky-1=0,所以y1+y2=![]() ,
,
所以![]() =
=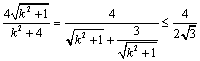 当且仅当k=
当且仅当k=![]() 时取“=”,所以S
时取“=”,所以S![]() =
=![]()