高二数学上学期综合测试1
班级＿＿＿＿姓名＿＿＿＿＿＿
一、选择题（本大题共12小题，每小题5分，共60分）
1、直线xcosα-y+1=0的倾斜角的取值范围是 ( )
A、[0º，90º] B、[0º，180º]
C、[45º，135º] D、[0º，45º]∪[135º，180º]
2、方程x+y=1表示的曲线是 ( )
A、一条直线 B、两条直线 C、正方形 D、四条直线
3、点A（2，1）关于直线x+y+1=0对称点的坐标是 ( )
A、（2，3） B、（2，—3） C、（—2，3） D、（—2，—3）
4、如果椭圆x2+ky2=2表示焦点在y轴上的椭圆，则实数k的取值范围是 ( )
A、(0，+∞) B、(0，2) C、(1，+∞) D、(0，1)
5、“ab<
表示双曲线”的（ ）
A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分又不必要条件
6、直线mx+y+2=0与线段MN有交点，其中M（—2，1），N（3，2），则实数m的取值范围是 ( )
A、
≤m≤
B、m≤或m≥ C、
≤m≤
D、m≤或m≥
7、圆
对称的圆的方程是 （ ）
A、
B、
C、
D、
8、已知点
和
，曲线上的动点P到
、
的距离之差为6，则曲线方程为（ ）
A、
B、
C、或
D、
9、动圆与两圆
和
都相切，则动圆圆心的轨迹为（ ）
A、抛物线 B、圆 C、双曲线的一支 D、椭圆
10、圆2x2+2y2=1与xsin
+y-1=0(
)的位置关系是
A、相交 B、相切 C、相离 D、不确定的
11、与椭圆
共焦点，且两准线间的距离为
的双曲线方程为 （ ）
A、
B、
C、
D、
12、若椭圆
和双曲线
有相同的焦点、，P是两曲线的一个公共点，则
的值是（ ）
A、m-a B、
C、
D、
二、填空题 （本大题共4小题，每小题5分，共20分）
13、抛物线x2-4y-3=0的焦点坐标为_________。
14、椭圆的两焦点把两准线间的距离三等分，则这个椭圆的离心率是_________。
15、已知点P是椭圆64x2+100y2=6400上的一点，F1, F2是焦点，∠F1PF2=60º，则ΔF1PF2的面积是 。
16、设F是椭圆
的右焦点，定点A(2,3)，点P在椭圆上，则PA+2PF的最小值是_________________。
三、解答题（本大题共5小题，每小题14分，共70分）
17、三角形的两条高所在直线方程为：2x -3y+1=0和x+y=0，点A(1，2)是它的一个顶点； 求：(1)BC边所在直线方程； (2)三个内角的大小。
18、圆x2+y2=8内有一点P(-1，2)，AB为过P且倾斜角为α的弦；
(1) 当α=135º时，求AB的长；
(2) 当弦AB被P平分时，写出直线AB的方程。
19、家具公司制作木质的书桌和椅子，需要木工和漆工两道工序。已知木工平均4小时做一把椅子，8个小时做一张书桌，该公司每星期木工最多有8000个工作时；漆工平均2小时漆一把椅子，1个小时漆一张书桌，该公司每星期漆工最多有1300个工作时。又已知制一把椅子和一张书桌的最大利润分别是15元和20元。根据以上条件，怎样安排生产能获得最大利润？
20、若直线l：y=kx-2交抛物线y2=8x于A、B两点，且AB的中点为M(2，y0)，求y0及弦AB的长。
21、设双曲线C的虚轴长、实轴长及焦距依次成等差数列，它的右准线为y轴，且双曲线C的右支过定点M(1,2)，求双曲线C的右顶点轨迹方程。
上学期
高二数学综合测试1参考答案
一、选择题：
1、D 2、C 3、D 4、D 5、A 6、D
7、B 8、D 9、C 10、C 11、A 12、A
二、填空题：
13、(0，
) 14、
15、
16、
-2
三、解答题：
17、(1) BC边所在直线方程为：2x+3y+7=0
(2) 
18、(1) 
(2) x-2y+5=0
19、解：设每星期安排生产椅子x把，书桌y张，利润为z元。
由题意得：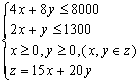
分析得出最优解
20、
21、