高二数学下期期中考试
班次: 学号: 姓名:
一、选择题（每小题3分，共36分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1．下面的结论中正确的是 ……………………………………………( )
A. 若a>b,则a2>b2 B. 若a>b而c∈R,则ac2>bc2
C. 若a>b,则
D.
若a>b,则a2>b2
2．已知直线L1和L2的斜率是方程
的两根，则L1与L2 所成的角是 ……………………………………………………（ ）
A．450 B．300 C．150 D．600
3．有下列命题：
（1）若两条直线平行，则其斜率必相等；
（2）若两条直线互相垂直，则其斜率的乘积必为－1；
（3）过点（－1，1），且斜率为2的直线方程是
；
（4）同垂直于x轴的两条直线一定都和y轴平行。
其中真命题的个数是 ………………………………………… （ ）
A．0 B．1 C．2 D
4、 不等式
的解集为………………………( )
A、
B、
C、
D、空集
5．如果AC<0,且BC<0,那么直线Ax+By+C=0一定不经过…( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6．若
均为大于1的正数，且
，则
的最大值是…………………………………………………………………（ ）
A. 2 B. 
C. 
D. 
7．已知直线C1：y=mx－1;线段C2：y=1,x≤1,要使C1与C2总有公共点，则实数m的取值范围是…………………………………（ ）
A．[－1，1] B．（－∞，1）
C．
D．
8．不等式
的解集是…………………………………（ ）
A.
B.
C.
D.
9．若直线:y=ax+2和直线y=3x-b关于直线y=x对称,则………( )
A.a=3,b=2 B.a=
,b=6 C.a=,b=-2 D.a=3,b=6
10．乘某种出租车,行程不足4千米时,车票为10.4元,行程大于或等于4千米而不足16千米的部分,每0.5千米车票0.8元.计程器每0.5千米计一次价,例如当行驶路程x(千米)满足12≤x<12.5时,按12.5千米计价;当12.5≤x<13时,按13千米计价.若某人乘车从A地到B地共付费28元,则从A地到B地行驶的路程m千米满足…………( )
A.10.5≤m<11 B.11≤m<11.5
C.14.5≤m<15 D.15≤m<15.5
11．两条平行线
和
之间的距离是（
）
A. 
B. 
C. 
D. 
12．下列函数中最小值是2的函数是…………………………( )
A. y=tgx+ctgx B.
y=
C. y=
D.
y=
二、填空题（每小题4分，共20分）
14.过点（－1，1）的所有直线中，与点（2，－1）距离最远的直线方程为 .
15、若2x+y=1, x>0,
y>0，则
的最小值是
.
16．若x,y满足约束条件: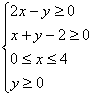 
, 则z=2x+y的最小值是
.
三、解答题（本大题共44分）
18.(此小题满分10分) 已知点A（2，3）、B（1，1）和直线
: 3x+4y+8=0,求满足下列条件的直线的方程：
①
经过点B,且与直线平行；
② 线段AB的中垂线方程;
③
过点A被两直线和
：3x+4y-7=0截得的线段CD长为
的直线方程。
19.(此题满分8分)已知a，b∈R +且a+b = 1，求证：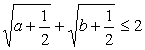
20．(此题8分)某工厂利用纳米技术,生产一种可随意弯曲的彩色魔幻广告灯管.现将长度为L米的一支直灯管弯曲成一个面积最大的扇形形状,试问这个扇形半径为多少米,其面积为多少?
21．(此题8分)解关于x的不等式:ax2-(a+1)x+1>0 (a>0)
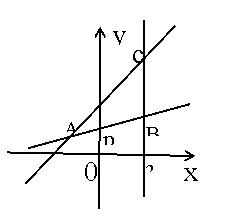22、(此题10分)如图，已知直线
过点P(0,1)，并与直线
：
和
：
分别交于点A、B，与交于点C，的斜率k小于1，
(1) 若
，求直线的方程.
(2) 若使
ABC面积最小，求直线的方程.