高二数学第二学期质检试题
一．选择题：
1、已知三条两两相交的直线，这三条直线最多可确定的平面个数为 （ ）
A． 4 B.
2．空间三条直线互相平行,由每两条平行线确定一个平面,则可确定平面的个数为（ ）
A．3 B．1或
3．若
为异面直线，直线c∥a，则c与b的位置关系是 （ ）
A．相交 B．异面 C．平行 D． 异面或相交
4．垂直于同一条直线的两直线的位置关系是 （ ）
A．平行 B.异面 C.平行、垂直或异面 D.相交、平行或异面
5．已知水平放置的△ABC按“斜二测画法”得到如图所示的直观图，
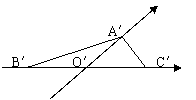其中B′O′=C′O′=1, A′O′=
,那么原△ABC是一个（ ）
A． 等边三角形
B． 直角三角形
C． 三边中有两边相等的等腰三角形
D． 三边互不相等的三角形
|
A．
B．
C．
D．
7．直线与平面平行的充要条件是这条直线与平面内的（ ）．
A．一条直线不相交 B．两条直线不相交
C．任意一条直线都不相交 D．无数条直线不相交
8．已知直线
（ ）
A．异面 B．相交 C．平行 D．不确定
9．用
表示一个平面，l表示一条直线，则平面内至少有一条直线与l（ ）
A．平行 B．相交 C．异面 D．垂直
10．已知A、B、C三点不共线，对平面ABC外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是 （ ）
A．
B．
C．
D．
11．设向量
是空间一个基底，则一定可以与向量
构成空间的另一个基底的向量是 （ ）
A．
B．
C．
D．
12．对空间任意两个向量
的重要条件是 （ ）
A．
B．
C．
D．
二．填空：
13、若a，b是异面直线，P是a，b外的一点，有以下四个命题：
①过P点可作直线k与a，b都相交;
②过P点可作平面与a，b都平行;
③过P点可作直线与a，b都垂直;
④过P点可作直线k与a，b所成角都等于50
.
这四个命题中正确命题的序号是_______
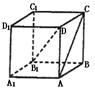
14、ABCD-A1B
，过P、M、N的平面交上底面于PQ，Q在CD上，则PQ=
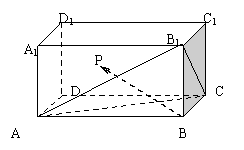15.如图,已知平行六面体ABCD—A1B
，则P点的位置关系有何特点
16、经过一个角的顶点引这个角所在平面的斜线，如果它和已知角两边的夹角为锐角且相等，那么这条斜射线在在平面内的射影是
三．解答题：
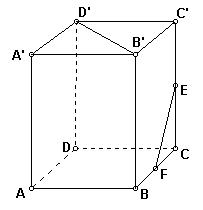
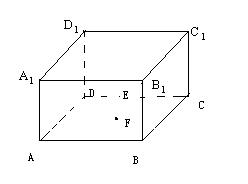
17、如图长方体中，AB=BC=1，AA′=2，E、F分别为棱中点。
（1） 写出所有与AA′垂直的棱；
（2） 求异面直线D′B′与EF所成角的余弦值。
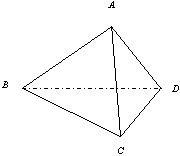
18、如图已知空间四边形ABCD中， 
，
证明：
.
 |
19、如图，长方体
中，E、F为面
上两点，过F在面上作直线
，并写出作法
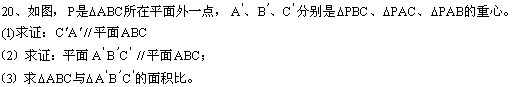
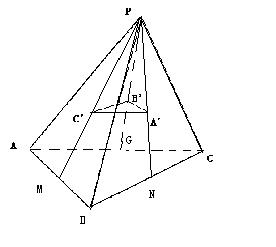
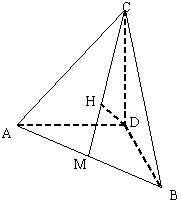21.已知等腰Rt△ABC中,∠ACB=90°,AC=2, 以AB边上的高CD为轴,把△ADC绕轴旋转至∠ADB=90°,并在AB上取中点M, 过D作DH⊥CM于H.
(1) 证明:DH⊥BC
(2) 求:异面直线BC与MD所成的角,
(3) 求:点D到平面ABC射影之间的距离.
一、选择题
1、B，2、C，3、D，4、D，5、A，6、D 7、C 8、C 9、D10、D 11、C12、D
二、填空题
13、③、④ 14、
15、点P在平面AB
三、解答题
17、（1）与AA′垂直的棱有：
AB、BC、CD、DA、A′B′、B′C′、C′D′、D′A′
（2）连结BC′，DB，DC′，在长方体中，有D′B′∥DB，由E、F为棱中点可知EF∥C′B，则可知∠DBC′即为所求的异面直线D′B′与EF所成的角，在△DBC′中，可求得：DB=
，BC′=DC′=
，所以，cos∠DBC′=
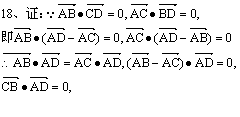
21、解:
(1) 连结MD,AC=BC,M为AB中点
所以CM⊥AB
又旋转前CD⊥AB,所在旋转后, CD⊥AD,CD⊥DB,且AD∩BD=D,所以CD⊥面ABD
又CM⊥AB,所以DM⊥AB(三垂线逆定理)
又CM∩DM=M,所以AB⊥面CMD
由已知DH⊥CM,所以DH⊥BC(三垂线定理)
(2) 取AC中点N, 连结MN,DN,
由M为AB中点,知MN∥
BC,所以∠DMN为异面直线BC与MD所成的角.
(求∠DMN过程略) ∠DMN=60°
(3) 由已知DH⊥CM,又由(1)知DH⊥BC,而且CM∩BC=C
所以DH⊥面ABC,由已知H是垂足,即H是D在平面ABC上的射影
故DH的长为等于点D到平面ABC射影之间的距离.
(求DH的长略)则DH=