高二数学第七章知识总结

	学科：数学
	教学内容：高二数学第七章 知识总结

知识总结:

1.确定直线方程需要有两个互相独立的条件，而其中一个必不可少的条件是直线必须经过一个已知点.确定直线方程的形式很多，但必须注意各种形式的直线方程的适用范围.

名  称	方  程	说  明	适用条件
点斜式	y-y0＝k(x-x0)	(x0,y0)——直线上已知点k——斜率	倾斜角为90°的直线不能用此式
两点式		(x1,y1)(x2,y2)是直线上两个已知点	与坐标轴平行的直线，不能用此式
一般式	Ax+By+C＝0	-——斜率 (0,-)——直线与y轴交点	A、B不同时为零

2.平面上的直线二元一次方程

3.两条直线的夹角，当两直线的斜率都存在且k₁·k₂≠-1时，tanθ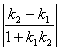＝，当直线斜率不存在时，应结合图形判断、求解，另外注意到角公式与夹角公式的区别.

4.判断两直线是否平行或垂直时，若两直线的斜率都存在，可用斜率的关系来判断.但若直线斜率不确定，则必须用一般式的平行垂直条件来判断.

5.在实际问题中，当我们求轨迹方程时，有时很难或不能找到曲线上点的坐标之间的直接关系.若引进适当的参数，问题往往比较容易解决.如研究运动的物体的轨迹时，常用时间作参数；研究旋转的物体的轨迹时，常用旋转角作参数.

6.化参数方程为普通方程的关键，在于消去参数.反之，选择适当的参数也可以将普通方程化为参数方程.

7.曲线与方程的关系，反映了现实世界空间形成和数据关系之间的某种联系，我们将曲线看作适合某种条件P的点M的集合P＝｛M｜P(M)｝.在建立坐标系后，点集P中任一元素M都有一个有序数对(x,y)和它对应，(x,y)是某个二元方程f(x,y)＝0的解，也就是说，它是解的集合Q＝｛(x,y)｜f(x,y)＝0｝中的一个元素，反之，对于解集Q中任一元素(x,y)，都有一点M与它对应，点M是点集P中的一个元素.P和Q的这种对应关系就是曲线和方程的关系.

8.根据圆的定义，求出了圆的标准方程.又由标准方程推出了圆的一般方程.圆的标准方程的优点，在于它明确地指出了圆心和半径，而圆的一般方程则突出了方程形式上的特点，它没有xy项，且x²、y²项的系数相等.

9.注意圆的参数方程的应用.

10.在学习中注意应用数形结合的数学思想，即把对把几何图形的研究，转化为对代数式的研究，同时又要理解代数问题的几何意义.