高二数学第一学期教学质量检测
试卷
| 题号 | 1-10 | 11-14 | 15 | 16 | 17 | 18 | 总 分 |
| 得分 |
说明：不能使用计算器；本试卷满分100分，在90分钟内完成
一、选择题：（本大题共10小题，每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
每题的4个答案中，只有一个是正确的，请把选出的答案编号填在上面的答题表中
1、设a>b>0，c>d>0，则下列不等式中不正确的是
A、ac>bd B、a-d>b-c C、a+c>b+d D、
2、若实数x，y满足
，则
的最小值是
A、12 B、4 C、8 D、7
3、过点（1，2）且与原点距离最大的直线方程是
A、x–2y+3=0 B、2x+y–4=0 C、x+3y–7=0 D、x+2y–5=0
4、已知直线l的倾斜角为α，若cosα= –
，则直线l的斜率为
A、
B、
C、– D、–
5、已知直线
，则直线l1和l2的夹角为
A、
B、
C、
D、
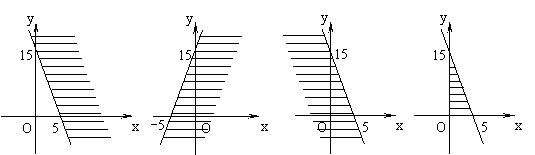6、不等式3x + y ≤15表示的平面区域为
A B C D
7、定长为6的线段，其端点分别在x轴和y轴上移动，则的中点M的轨迹方程是
A、x + y= 6 B、x2 + y2 = 9 C、2x2 + y2 =12 D、x2 + 2y2 =12
8、方程
表示焦点在y轴上的椭圆，则k的整数值有
A、1个 B、2个 C、3个 D、4个
9、顶点在x轴上，两顶点间的距离为8， e =
的双曲线的标准方程为
A、
B、
C、
D、
10、抛物线
上有一点P，P到椭圆
的左顶点的距离的最小值为
A、
B、2+
C、
D、
二、填空题：（本大题共4小题，每小题4分，共16分）
11、不等式
的解集为_________________；
12、两平行直线3x－2y＋4＝0与3 x－2y = 0 之间的距离等于 ；
13、已知圆的参数方程为
，化成圆的一般方程是_________________；
14、2003年10月15日我国成功发射了“神州五号”载人飞船，飞船运行轨迹是以地心 为一个焦点的椭圆，其近地点距地面400 km，远地点距地面800 km，已知地球半径近似为6400 km，现建立一个坐标系，设地心在横轴上且为该椭圆的右焦点，请写出该轨迹的标准方程（以100km为1个单位） .
__________________________
三、解答题：（第15题14分、16题8分，第17题10分，第18题12分，共44分）.
15、（1）解不等式： x2+3x-8 <10；
解：
（2）设a，b，c，d都是实数，且a2+b2=1，c2+d2 =1，证明：ac+bd≤1
证明：
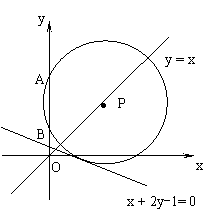16、圆心P在直线y = x上，且与直线x + 2y-1= 0相切的圆，截y轴的上半轴所得的弦 AB长为2，如图所示，求此圆的方程．
解：
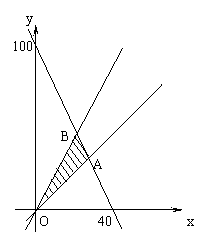
17、景新中学高二（3）班同学捐款2000元，准备为“福源希望小学”购买单价为50元的课桌和20元的椅子，若要使桌椅的总数尽可能多，但椅子数不能少于桌子数，且不多于桌子数的1.5倍，问桌椅各买多少才合适. （要求画出示意图）
解：
18、已知椭圆
（a>b>0）的一条准线方程是
其左、右顶点分别是A、B；双曲线
的一条渐近线方程为3x－5y=0.
（1）求椭圆C1的方程及双曲线C2的离心率；
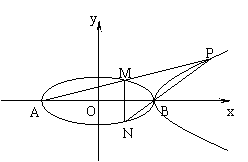
（2）在第一象限内取双曲线C2上一点P，连结AP交椭圆C1于点M，连结PB并延长交椭圆C1于点N，若点M是线段AP的中点. 求证：MN⊥AB
 |
高二数学第一学期教学质量检测参考答案
一、选择题：（本大题共10小题，每小题4分，共40分）
DCDCA CBBAA
二、填空题：（本大题共4小题，每小题4分，共16分）
11、{x-2<x<4}； 12、
； 13、x2+y2+4x-2y+2=0； 14、
.
三、解答题：（第15题14分、16题8分，第17题10分，第18题12分，共44分）.
15、（1）解：原不等式等价与
，…………………………………………………………2分
|
…………………………………………………………2分
由①得：-6<x<3；由②得：x<-2或x>-1 …………………………………………………………2分
所以原不等式的解集为{x-6<x<-2或-1<x<3} …………………………………………………………1分
（2）证明：∵a、b、c、d都是实数，
∴ ac +bd ≤ ac + bd …………………………………………………………2分
≤
…………………………………………………………3分
=
=
…………………………………………………………2分
16、解：∵圆心P在直线y = x上，∴可设P的坐标为（k，k），
作PQ⊥AB于Q，连接AP，在Rt△APQ中，AQ=1，AP=r，PQ=k
∴r=
…………………………2分
又r=点P到直线x + 2y-1= 0的距离
∴
………………………2分
整理，得
解得，k=2或
（舍去） ………………………1分
∵所求圆的半径为
=
………………………1分
∴所求圆的方程为：
…………………2分
（第17题图）
17、解：设桌椅分别买x，y张，z = x + y
由题意得：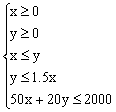
…………………………………………………………5分
满足以上不等式组所表示的区域是以A(
，)，B(25，37.5)，O(0，0)为顶点的△AOB内部.（如图所示）。
………………………………………………………………2分
对△AOB内的点P（x，y），z = x + y，即y=-x+z，这是斜率为-1，在y轴上截距为z的平行直线系。
要使z最大，只有点P与B重合即可，得x=25，y=37.5，但
，∴取y=37…………………2分
所以买桌子25张，椅子37张时是最优选择.
答：应买桌子25张，椅子37张。 …………………………………………………1分
18、解：（1）由已知
……………………………………………3分
∴椭圆的方程为
，
…………………………………………1分
∵双曲线的方程为
，又
∴双曲线的离心率
…………………………………………2分
（2）由（1）A（－5，0），B（5，0）
设M
，∵M为AP的中点，∴P点坐标可设为
将M、P坐标代入C1、C2方程得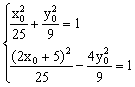
……………………………1分
消去y0得 
，解之得
，即xM =
……………1分
∴点P的坐标为（10，
…………………………………………………………1分
由P（10，，B（5，0），得直线PB：
，即
………1分
求直线PB：与椭圆：
的交点的横坐标，
得
，xN =…………………………………………………1分
∵xM = xN=，∴MN⊥x轴，即MN⊥AB………………………………………………………1分