高二数学第一学期教学质量检测试卷
| 题号 | 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
注:所有计算问题均可使用计算器;本试卷满分150分,在120分钟内完成
一、选择题:(每题5分,共60分,将答案直接填在下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1、已知a lg![]() >0,且a+b>0,则有
>0,且a+b>0,则有
A、![]() >0 B、
>0 B、![]() <
<![]() ≥0 D、
≥0 D、![]() ≤0
≤0
2、不等式![]() <0的解集是
<0的解集是
A、{x![]() 或
或![]() } B、{x
} B、{x![]() 或
或![]() }
}
C、{x ![]() } D、{x
} D、{x![]() 或
或![]() }
}
3、不等式![]() -3<1的解集是
-3<1的解集是
A、{ x 5 < x <16 } B、{x 6 < x < 18} C、{x 7 < x <20} D、{x 8 < x < 22}
4、直线l:![]() x+y-1=0 的倾斜角是
x+y-1=0 的倾斜角是
A、30º B、60º C、150º D、120º
5、直线3x-2y=4 的截距式方程是
A、![]() B、
B、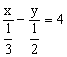 C、
C、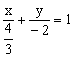 D、
D、![]()
6、两条直线mx+y-n=0和x+my+1=0互相平行的条件是
A、m=1
B、m=±![]() D、
D、![]() 或
或![]()
7、若![]() <-1,则方程bx2-ay2=b的曲线是
<-1,则方程bx2-ay2=b的曲线是
A、焦点在x轴上的椭圆 B、焦点在x轴上的双曲线
C、焦点在y轴上的椭圆 D、焦点在y轴上的双曲线翰林汇
 8、方程x=
8、方程x=![]() +1的曲线是
+1的曲线是
A B C D
翰林汇翰林汇9、下列各点中不在曲线上x2+y2-2mx+2my=0(m≠0)上的点是
A、(0,
10翰林汇、在直角坐标系中,与两坐标轴都相切的圆的圆心轨迹方程是
A、y=x B、y=x(x≠0) C、x2-y2=0 D、x2-y2=0(x≠0)
11、参数方程![]() (α为参数)所表示的曲线是:
(α为参数)所表示的曲线是:
A、圆 B、椭圆 C、直线 D、抛物线的一部分
12、如果椭圆的两条准线间的距离是这个椭圆的焦距的两倍,那么这个椭圆的离心率为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:(每题4分,共16分,将答案直接填在下表中)
| 题号 | 13 | 14 | 15 | 16 |
| 答案 |
13、过点(1,1)圆(x-1)2+(y-2)2 = 1的切线方程是______________________.
翰林汇14、等腰三角形ABC的底边的两个顶点是B(2,4)和C(3,-5),则顶点A的轨迹方
程为 .
15、抛物线y=x2上到2x-y=4距离最近的点的坐标是_______________.
16、对于椭圆![]() 和双曲线
和双曲线![]() 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是 .
三、解答题:(第17题16分,第18题10分,其它题各12分,共74分)
17、(1)已知x、y、z∈R,且x+y+z=a,求证:x2+y2+z2≥![]()
(2)已知a<0,求1![]() 的最值.
的最值.
解:
18、已知直线l1:![]() ,直线l2经过点P(0,1),且l2到l1的角为30º,求直线l2的方程.
,直线l2经过点P(0,1),且l2到l1的角为30º,求直线l2的方程.
解:
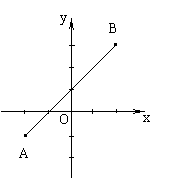 19、如图,已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围.
19、如图,已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围.
解:
20、(2)班在本届校运会上获团体冠军,学校奖励该班550元,并要求专款专用。经班委会研究决定,将奖金用于购买单价分别为60元、70元的足球和篮球,特别强调:足球至少买3个,篮球至少买2个。由体育委员陈鹏执行,请问陈鹏有多少种不同的购球方式?足球与篮球各买多少个,可以使剩下的钱最少?
解:
21、已知圆C关于y轴对称,经过抛物线![]() 的焦点,且被直线y=x分成两段弧长之比为1:2,求圆C的方程.
的焦点,且被直线y=x分成两段弧长之比为1:2,求圆C的方程.
解:
22、双曲线![]() 的右支上存在与右焦点和左准线等距离的点,求离心率e的取值范围.
的右支上存在与右焦点和左准线等距离的点,求离心率e的取值范围.
解:
参考答案
一、选择题:(每题5分,共60分,将答案直接填在下表中)
BABDC DCBAD AC
二、填空题:(每题4分,共16分,将答案直接填在下表中)
13、y =1 14、x-9y-7=0![]() 15、(1,1) 16、①②
15、(1,1) 16、①②
为方便计分,以下各题标注的分为步骤分,而非累积得分
三、解答题:(第17题16分,第18题10分,其它题各12分,共74分)
17、(1)证明:∵x+y+z=a,∴x2+y2≥2xy,y2+z2≥2yz,x2+z2≥2xz …………3分
∵x+y+z=a,∴a2=(x+y+z)2= x2+y2+z2+2xy+2yz+2xz≤3(x2+y2+z2) ………3分
∴x2+y2+z2≥![]() ………2分
………2分
(2)解:当a<0时,![]() >0,
………2分
>0,
………2分
∵(-![]() )=6为定值
…………2分
)=6为定值
…………2分
又∵当且仅当![]() ,即a=
,即a=![]() 时,
时,![]() 有最小值为
有最小值为![]()
∴1![]() 有最小值为1+
有最小值为1+![]() ………4分
………4分
18、解:已知直线l1的斜率为k1=![]() ,设直线l2的方程为y=k2x+b,
,设直线l2的方程为y=k2x+b,
∵k1=![]() ,∴l1的倾斜角为60º,
,∴l1的倾斜角为60º,
又l2到l1的角为30º,∴0<k2<k1,且l1与l2的夹角是30º ……………2分
∴tanα=![]() ,∴tan30º=
,∴tan30º=![]()
解之得:k2=![]() …………5分
…………5分
∵直线l2经过点P(0,1),∴b=1 ……………2分
∴直线l2的方程为y=![]() x+1
…………1分
x+1
…………1分
19、解:∵过点A、B的直线方程为在l:x-y+1 = 0 ……2分
作OP垂直AB于点P,连结OB
由图象得:m<OP或m>OB时,线段AB与圆x2+y2 = m2无交点. ……………2分
(I)当m<OP时,由点到直线的距离公式得:
![]() ,即
,即![]() .
……………3分
.
……………3分
(II)当m>OB时
![]() 即
即 ![]() . ………………3分
. ………………3分
∴当![]() 和
和![]() 时,圆x2+y2 = m2与线段AB无交点。 ………2分
时,圆x2+y2 = m2与线段AB无交点。 ………2分
20、解;设购买足球x个,篮球 y个,
依题意得: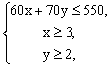 即
即 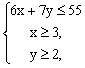 …………………………………………3分
…………………………………………3分
画出可行域,找到整点为:
(3,2),(3,3),(3,4),(3,5),(4,2),(4,3),(4,4),(5,2),(5,3),(6,2) 在可行域中,即陈鹏有10种不同的购球方式。 ………………6分
其中点(3,5)使目标函数u= 6x+7y 取最大值umax=53
∴买3个足球、5个篮球,可以使剩下的钱最少。 ………………………3分
21、解:设圆C的方程为![]()
![]() ,抛物线
,抛物线![]() 的焦点F(1,0)………………2分
的焦点F(1,0)………………2分
![]() ①
……………………3分
①
……………………3分
又直线y=x分圆的两段弧长之比为1:2,可知圆心到直线y=x的距离等于半径的![]()
即![]() ②
…………………3分
②
…………………3分
解①、②得![]() 故所求圆的方程为
故所求圆的方程为 ![]() ………4分
………4分
22、解:设M(x0,y0)是双曲线右支上满足条件的点,且它到右焦点F2的距离等于它到左准线的距离![]()
即![]() ,由双曲线定义可知
,由双曲线定义可知 ![]() …………………2分
…………………2分
∴![]() …………………………2分
…………………………2分
推导由焦点半径公式得 ![]() …………………………2分
…………………………2分
∴x0![]() ………………………2分
………………………2分
而![]() 即
即 ![]() …………………………………2分
…………………………………2分
解得![]() 但
但 ![]() …………………2分
…………………2分