试卷类型:A
高二数学调研测试题2
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至2页,第Ⅱ卷3至8页,共150分,考试时间120分钟.
第 Ⅰ 卷 (选择题,共60分)
注意事项:
1.请考生将自己的姓名、学号、班级填写在第Ⅱ卷的密封线内.
2.每小题选出答案后在第Ⅱ卷前的答题栏内用2B铅笔把对应题目的答案代号涂黑,不能答在试题卷上.
一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.
设a = (1,0,-1),b = (2,3,x),且a⊥b,则x的值是
A.0 B.![]() C.2 D.-2
C.2 D.-2
2.
4×5×6×……×(n-1)×n =
A.![]() B.
B.![]() C.n!-3! D.
C.n!-3! D.![]()
3.
已知![]() ,则n的值为
,则n的值为
A.8 B.6 C.4 D.3
4.
两个事件互斥是这两个事件对立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
5.
两平行直线x-y+1 = 0,x-y-1 = 0间的距离是
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
6.
空间四边形ABCD中,M、N是BC、CD的中点,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.
已知a、b、c是空间三条直线,![]() 是两个平面,则下列命题中正确的是
是两个平面,则下列命题中正确的是
A.若![]() ,则a∥b
,则a∥b
B.若![]() ,b⊥
,b⊥![]() ,则
,则![]()
C.若c是a在![]() 内的射影,且b⊥c,则a⊥b
内的射影,且b⊥c,则a⊥b
D.若![]() ,c∥
,c∥![]() ,则b∥c
,则b∥c
8.
若a、b是任意实数,且a>b,则
A.a 2>b2 B.![]() C.lg(a-b)>0 D.
C.lg(a-b)>0 D.![]()
9.
以一个三棱柱的顶点为顶点的四面体共有
A.6个 B.8个 C.12个 D.15个
10. 有以下三个命题:
①三个非零向量a、b、c不能构成空间的一个基底,则a、b、c共面
②若两非零向量a、b与任何一个向量都不能构成空间的一个基底,则a、b共线
③若a、b是两个不共线的向量,而![]() (
(![]() ∈R且
∈R且![]() ≠0),则{a,b,c}构成空间的一个基底
≠0),则{a,b,c}构成空间的一个基底
其中真命题的个数是
A.0 B.1 C.2 D.3
11. 已知圆C:x2+y2 =
1,点A(-2,0)及点B(2,a),从A点观察B点,要使视线不被圆C挡住,则a的取值范围是
A.(-∞,-1)∪(-1,+∞) B.(-∞,-2)∪(2,+∞)
C.(-∞,-![]() )∪(
)∪(![]() ,+∞) D.(-∞,-4)∪(4,+∞)
,+∞) D.(-∞,-4)∪(4,+∞)
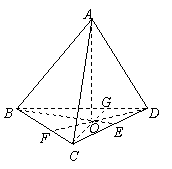
12. 在正四面体P-ABC中,G是△ABC的重心,F是△PAB的重心,D为PB上一点,E为BC的中点,若![]() ,则数
,则数![]() 的值为
的值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅰ卷答题栏
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 12 | 13 | 14 | 15 | ||||
[ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | [ A ] | ||||
[ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | [ B ] | ||||
[ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | [ C ] | ||||
| [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] | [ D ] |
高中调研测试题
高 二 数 学
第 Ⅱ 卷 (非选择题,共90分)
注意事项:
第Ⅱ卷共6页,用钢笔或圆珠笔直接答在试题卷中,答卷前将密封线内的项目填写清楚.
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
| 得分 | 评卷人 |
二.填空题:本大题共4小题,每小题4分,共16分.将正确答案填在题中横线上.
13. 球面面积膨胀为原来的4倍,则体积膨胀为原来的 倍.
14.
不等式![]() 的解集是 .
的解集是 .
15. 甲、乙两人独立地解同一问题,甲解对的概率是p1,乙解对的概率是p2,那么至多有一人解对这个问题的概率是 .
16.
(a1+a2)(b1+b2+b3)(c1+c2+c3+c4)展开式中,形如axbxcx的项称为标准项,形如axbxcy、axbycx、aybxcx
(x≠y) 的项称为次标准项,如a2b
三.解答题:本大题共6小题,满分74分.
| 得分 | 评卷人 |
17.
(本大题满分12分)求![]() 的展开式中,系数的绝对值最大的项和系数最大的项.
的展开式中,系数的绝对值最大的项和系数最大的项.
| 得分 | 评卷人 |
|
|
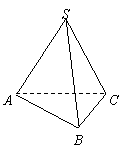
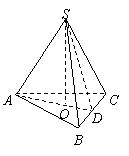
18. (本大题满分12分)正三棱锥S-ABC的底面边长为2,侧棱与底面所成的角为60°,求它的高和斜高.
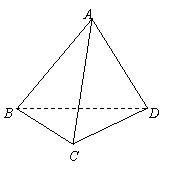
19. (本大题满分12分) 如图,一空间四边形ABCD的对边AB与CD互相垂直,AD与BC互相垂直,证明对角线AC与BD也互相垂直.
| 得分 | 评卷人 |
|
|
20.
(本大题满分12分)××市政府实施“景观工程”,对现有平顶的民用多层住宅进行“平改坡”,计划将平顶房屋改为尖顶,并铺上彩色瓦片.现对某栋房屋有如下两种改造方案:
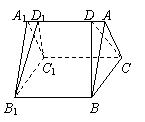
方案一:坡顶如图1所示,为顶面是等腰三角形(AB = AC)的直三棱柱,尖顶屋脊AA1与房屋长度BB1等长,有两个坡面需铺上瓦片.
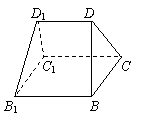
方案二:坡顶如图2所示,为由图1消去两端相同的两个三棱锥D-ABC、D1-A1B
若房屋长度BB1 =
| 得分 | 评卷人 |
|
|
21.
(本大题满分12分)在一次三人象棋对抗赛里,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛顺序如下:第一局:甲对乙;第二局:第一局的胜者对丙;第三局:第二局的胜者对第一局的负者;第四局:第三局的胜者对第二局的负者.求:
(1)乙连胜四局的概率;
(2)丙连胜三局的概率.
| 得分 | 评卷人 |
22.
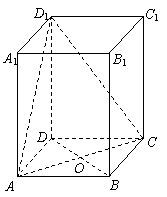
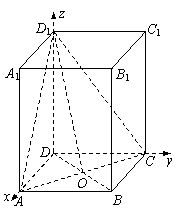
(本大题满分14分)如图,在长方体ABCD-A1B![]() .
.
(1)求此长方体的体积;
(2)求截面D
(3)在棱B1B上找一点P,使得PD⊥平面D
| 得分 | 评卷人 |
|
|
高二数学调研测试题参考答案及评分标准
一.选择题:CBCBB ABBCC CD
二.填空题:13.8 14.{x|-2≤x<2} 15.1-p1p2 16.![]()
三.解答题:
17.解:展开式的通项是![]() 2分
2分
系数的绝对值是![]() ,若它最大,则
,若它最大,则
![]() 即
即 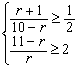 6分
6分
解得:![]()
∵r∈N ∴r = 3
故系数绝对值最大的项是第4项,即![]() 8分
8分
系数最大的项应在项数为奇数的各项之内,即r取偶数0,2,4,6,8时的各项系数
分别为![]()
即1,![]()
∴系数最大的项是第5项,即![]() 12分
12分
|
|
18.解:过S作SO⊥底面ABC于点O,则点O是△ABC的中心,∠SAO是侧棱SA与底面ABC所成的角 2分
∴∠SAO = 60°
连结AO交BC于D,连结SD,则SD⊥BC
在正△ABC中,![]()
∴![]()
故SO = AO×tan 60°= 2 6分
![]()
![]()
∴正三棱锥的高为2,斜高为![]() . 12分
. 12分
|
|
19.证法一:∵AB⊥CD,∴![]() 0
0
即![]() 0
0
Þ ![]() ① 4分
① 4分
∴AD⊥BC,∴![]() 0
0
即![]()
Þ ![]() ② 8分
② 8分
由①、②得:![]() Þ
Þ ![]()
即![]() 0 ∴AC⊥BD. 12分
0 ∴AC⊥BD. 12分
证法二:过点A作AO⊥平面BCD于点O,连结BO、DO、CO并延长分别交CD、BC、BD于E、F、G,则BE、DF、CG分别是AB、AD、AC在底面BCD上的射影 4分
∵AB⊥CD,由三垂线定理得:BE⊥CD
同理DF⊥BC 8分
∴点O是△BCD的垂心,故CG⊥BC
由三垂线定理的逆定理知:AC⊥BD. 12分
20.解:要比较两种尖顶铺设的瓦片量,只要比较△ABD和△ACD的面积之和与△BCD的面积的大小. 2分
作AE⊥BC于E点,则AE⊥平面B1BCC1,故AE = h
∴AB = ![]()
设AD长为x,则DE = ![]()
∴![]()
![]()
![]() 8分
8分
当x>b,即AD之长大于房屋宽度的一半时,图2尖顶铺设的瓦片较省
当x=b,即AD之长等于房屋宽度的一半时,两种尖顶铺设的瓦片相同
当x<b,即AD之长小于房屋宽度的一半时,图1尖顶铺设的瓦片较省. 12分
 21.解:(1)乙连胜4局,必须每局乙都是胜者
21.解:(1)乙连胜4局,必须每局乙都是胜者
故四局的胜负情况为:第一局乙胜,甲负;第二局乙胜,丙负;第三局乙胜,甲负;第四局乙胜,丙负; 2分
∴乙连胜4局的概率为(1-0.4)×0.5×(1-0.4)×0.5 = 0.09 4分
(2)丙连胜三局的情况有两种情形
①第一局甲胜,乙负;第二局丙胜,甲负;第三局丙胜,乙负;第四局丙胜,甲负
其概率为0.4×0.6×(1-0.5)×0.6 7分
②第一局乙胜,甲负;第二局丙胜,乙负;第三局丙胜,甲负;第四局丙胜,乙负
其概率为(1-0.4)×(1-0.5)×0.6×(1-0.5) 10分
∴丙连胜三局的概率为
0.4×0.6×(1-0.5)×0.6+(1-0.4)×(1-0.5)×0.6×(1-0.5) = 0.162. 12分
22.方法一:
(1)解:设![]() i,
i,![]() j,
j,![]() k (h>0),以i,j,k为坐标向量建立空间直角坐标系D-xyz.
k (h>0),以i,j,k为坐标向量建立空间直角坐标系D-xyz.
则A(2,0,0),B (2,2,0),C (0,2,0),
D1(0,0,h)
3分
∴![]() (2,2,0),
(2,2,0),![]() (0,2,-h)
(0,2,-h)
![]()
∴![]() ,解得:h = 4
,解得:h = 4
故V = 2×2×4 = 16 6分
(2)由于底面ABCD是正方形,∴AC⊥BD,
由三垂线定理知,D1O⊥AC
∴∠D1OD是所求二面角的平面角 8分
![]() (-1,-1,4),
(-1,-1,4),![]() (-1,-1,0)
(-1,-1,0)
![]()
∴所求二面角的大小为![]() . 10分
. 10分
(3)解:设P(2,2,z),则![]() (2,2,z) ,
(2,2,z) ,![]() (2,0,-4),
(2,0,-4),![]() (0,2,-4)
(0,2,-4)
令![]() ,即2×2+0×2+(-4)×z = 0,得z = 1
,即2×2+0×2+(-4)×z = 0,得z = 1
∴当BP = 1时,DP⊥平面D
方法二:
(1)连结A1B,则A1B∥CD1,故∠A1BD是异面直线DE与D
设DD1 = x,则A1D = A1B = ![]() ,BD =
,BD = ![]()
∴cos∠A1BD = ![]() 4分
4分
∴![]() Þ x = 4
Þ x = 4
故V = 2×2×4 = 16 6分
(2)由于底面ABCD是正方形,∴AC⊥BD,
由三垂线定理知,D1O⊥AC
∴∠D1OD是所求二面角的平面角 8分
在Rt△D1DO中,![]()
∴所求二面角的大小为![]() . 10分
. 10分
(3)设BP = x,由于BP⊥AC,故要PD⊥平面D
这时,Rt△D1DO∽Rt△DBP,∴![]() 12分
12分
解得:x = 1
∴当BP = 1时,DP⊥平面D