高二数学段考试题

高二数学段考试题

班别　　 姓名　

题号	一	二	三						总分
			17	18	19	20	21	22
得分

一、选择题（本大题共12小题，每小题5分，共60分）

1．平行四边形ABCD的相邻两边AB与BC的长分别为a和b，将平行四边形分别绕AB和BC旋转一周，形成两个几何体，它们的体积之比是　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　D．

2．长方体的全面积为72，则长方体的对角线长的最小值是　　　　　　　　　　　　　　　　　　（　　）

　　　 A．6　　　　　　　　　　　　B．6　　　　　　　　　C．12　　　　　　　　　　　D．12

3．设M、O、A、B、C是空间的点，则使M、A、B、C一定共面的等式是　　　　　　（　　）

　　　 A．　　　　　　　　B．

　　　 C．　　　　　　D．

4．正六棱柱AC₁的所有棱长均为1，过棱AB和D₁E₁作截面，则此截面的面积是（　　）

　　　 A．2　　　　　　　　　　　　B．3　　　　　　　　　　　　C．　　　　　　　 D．

5．正四棱锥S—ABCD中，BC=6，SA=5，那么SA和BC的间距为　　　　　　　　　　　　 （　　）

　　　 A．4　　　　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　D．

6．设地球半径为Rkm，在地球北纬30°圈上有甲、乙两个卫星地面接受站，它们的球面距离为km，则甲、乙两地的经度差满足　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　 B． C．　　　　　 D．

7．已知　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．90°　　　　　　　　　 B．30°　　　　　　　　　 C．60°　　　　　　　　　 D．150°

8．如图，一正方体棱长为3cm，在每个面正中央有一个入口为正方形的孔通到对面，孔的边长为1cm，孔的各棱平行于正方体各棱，则所得几何体的总表面积为　　　　　　　　　　　　　　　　（　　）

　　　 A．54cm²　　　　　　　　 B．72cm²　　　　　　　　

　　　 C．76cm²　　　　　　　　 D．84cm²

9．圆锥的母线长为l，高为h，，如果过圆锥顶点的截面的最大值为，则　　　　　　（　　）

　　　 A．　　　　　　　　　　　　　　　　　　　　　　B．　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　D．

10．已知点A（1，0，0），B（0，1，0），C（0，0，1），若存在点D，使得DB∥AC，DC∥AB，则D点的坐标是　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．（-1，1，1）　　　　　　　　　　　　　　　　　　　 B．

　　　 C．（-1，1，1）或（1，-1，-1）　　　　　　 D．

11．已知球的半径为R，则该球内接圆锥体积的最大值是　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　B．　　　　　　　C．　　　　　　　D．

12．a，b表示不同的直线，表示不同的平面，有下面四个命题　　　　　　　　　 （　　）

　　　 ①若

　　　 ②若

　　　 ③

　　　 ④

　　　 上述四个命题中，正确的命题序号是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①④　　　　　　　　　 B．①③　　　　　　　　　 C．②④　　　　　　　　　 D．④

二、填空题（本大题共4小题，每小题4分，共16分）

13．棱锥的底面是一个锐角为30°，斜边长为2的直角三角形，并且各侧面和底面都成60°的二面角，则此棱锥的全面积为 　　　　　　　　　　　 .

14．在三棱锥S—ABC中，∠ASC=∠BSC=30°，∠ASB=45°，二面角A—SC—B的平面角的余弦值为 　　　　　　　　　　　 .

15．已知A（1，-1，3），B（0，2，0），C（-1，0，1）若点D在OZ轴上，且

　　　 则 　　　　　　　　　　　 .

16．将边长为a的正方形剪去图中的阴影部分（如图），再沿图中虚线折成一个正三棱锥，这个正三棱锥与底面所成角的余弦值是 　　　　　　　　　　　 .

三、解答题（本大题共6题，共74分）

17．已知：为空间两个向量，求证，当且仅当时，等号成立。（12分）

18．圆锥的内切半球的大圆在圆锥底面上，已知圆锥的全面积与半球的面积之比为18：5，如图，求圆锥的底面半径与母线长之比。（12分）

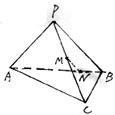
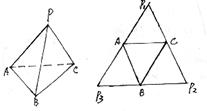
19．三棱锥P—ABC中，PA=PB，CB⊥面PAB，M、N分别在PC、AB上，且PM=MC，AN=3NB

（1）求证：MN⊥AB　（2）当∠APB=90°，BC=2，AB=4时，求MN的长。（12分）

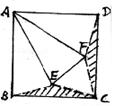
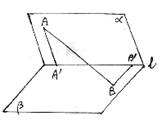
20．如图，二面角，。

　　　 若

（1）求；

（2）求AB与l所成的角.(12分)

21．如图，将四面体P—ABC沿PA，PB，PC剪开展平，恰好得

（1）求证：四面体P—ABC中，PA⊥BC；

（2）若P₁P₂=26，P₁P₃=20，求四面体的体积（12分）

22．已知斜三棱柱ABC—A₁B₁C₁中，AB=AC=a，∠BAC=90°，顶点A₁在底面ABC上的射影M为BC的中点，且点M到侧面AA₁B₁B的距离为，

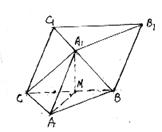
（1）求证平面A₁AM⊥平面A₁BC；

（2）求二面角A₁—AB—C的大小；

（3）求；

（4）求点B到平面ACC₁A₁的距离.(14分)

高二数学段考试题参考答案

一、选择题

1．B　2．A　3．D　4．B　5．D　6．D　7．D　8．B　9．C　10．A　11．B　12．D

二、填空题13．　　14．　　15．　　 16．

三、解答题

17．证明

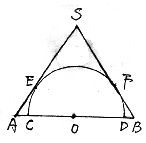
18．解：设圆锥的底面半径为r，母线长为l，球半径为R，

作圆锥的轴截面SAB，E、F为切点，

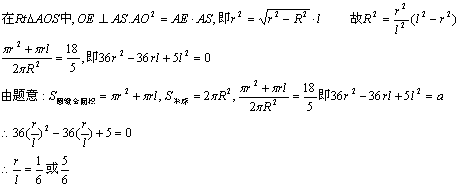
19．解：设

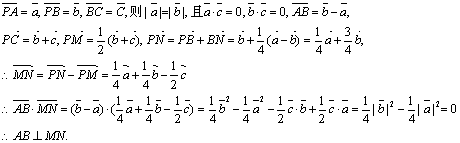
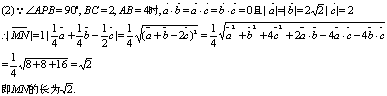
20．解：

21．解：（1）由题知A，B，C是△P₁P₂P₃各边中点，∵P₁P₂=P₂P₃

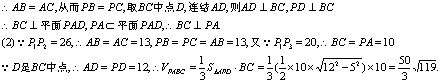
22．解（1）证