高二数学寒假综合测试（一）
数学试题卷
考生须知：本卷分卷Ⅰ卷Ⅱ，均做在答题卷上，本卷满分150分，时间120分钟
第Ⅰ卷（选择题，共60分）
一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
（1）若
的定义域为M，
的定义域为N，令全集I=R，则
（A）M （B）N （C）
（D）
（2）已知数列
中，
，则这个数列前n项和的极限是
（A）2 （B）
（C）3 （D）
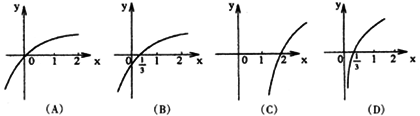
（3）已知函数
，则它的反函数
的图象是
（4）圆台的轴截面面积与侧面积的比为
，则侧面母线所在直线与轴所夹锐角为
（A）arccos
（B）arccos
（C） （D）
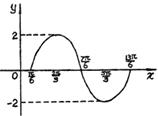
（5）函数
）图象的两条相邻对称轴之间的距离是
（A） 
（B）
（C）
（D）
（6）从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植，不同的种植方法共有 A．24种 B．18种 C．12种 D．6种
（7）已知A、B、C、D为同一球面上的四点，且连接每两点间的线段长都等于2，则球心O到平面BCD的距离等于
（A）
（B）
（C）
（D）
（8）定义在（-∞，+∞）上的函数y=f(x)在（–∞，2）上是增函数，且函数y=f(x+2)图象的对称轴是x=0，则
（A）f(–1)<f(3) （B）f(0)>f(3) （C）f(–1)=f(–3) （D）f(2)<f(3)
（9）若圆
上有且仅有两个点到直线4x+3y=11的距离等于1，则半径R 的取值范围是
（A）R>1 （B）R<3 （C）1<R<3 （D）R≠2
（10）原市话资费为每3分钟0.18元，现调整为前3分钟资费为0.22元，超过3分钟，每分钟按0.11元计费，与调整前相比，一次通话提价的百分比
（A）不会高于70% （B）会高于70%而不会高于90%
(C)不会低于10% （D）高于30%而低于100%
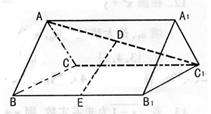
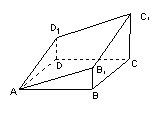
（11）图中多面体是过正四棱柱的底面正方形ABCD的点A作截面
而截得的，且
.已知截面与底面ABCD成30°的二面角，AB=1，则这个多面体的体积为
（A）
（B）
（C）
（D）
（12）已知双曲线
（a>0,b>0）的离心率
, 令双曲线两条渐近线构成的角中，以实轴为角平分线的角为
，则的取值范围是
（A）
（B）
（C）
（D）
寒假综合测试（一）
数学答题卷
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
第II卷（非选择题共90分）
二、填空题：本大题共4小题，每小题4分，共16分.
（13）若
展开式中的第5项为常数，则n=
.
（14）抛物线
的准线方程是
.
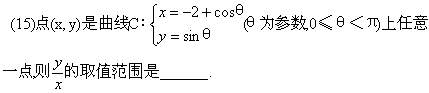
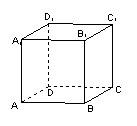
（16）已知如图，正方体ABCD–
，过点A作截面，使正方体的12条棱所在直线与截面所成的角皆相等，试写出满足这样条件的一个截面
.（注：只需任意写出一个.）
三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤
（17）（本小题满分12分）已知
，求使
成立的自变量x的取值范围.
（18）（本小题满分12分）已知函数
的图象在y轴上的截距为1，它在y轴右侧的第一个最大值点和最小值点分别为（
）和（
）.
（I）求
的解析式；
(II）将y=f(x)图象上所有点的横坐标缩短到原来的（纵坐标不变），然后再将所得图象向x轴正方向平移
个单位，得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画出y=g(x)在长度为一个周期的闭区间上的图象.
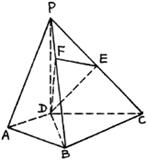
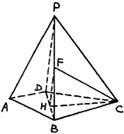
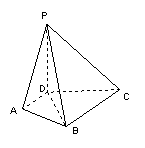（19）（本小题满分12分） 已知：如图，PD⊥平面ABCD，AD⊥DC，AD∥BC，
.
（Ⅰ）求PB与平面PDC所成角的大小；
（Ⅱ）求二面角D–PB–C的正切值；
（III）若
，求证平面PAB⊥平面PBC.
（20）（本小题满分12分）已知椭圆的两个焦点分别为
，离心率
（Ⅰ）求椭圆方程；
（Ⅱ）一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N，且组段MN中点的横坐标为–，求直线l倾斜角的取值范围.
21、（本题满分12分）
如图，在正三棱柱ABC—A1B1C1中，各棱长都相等，D、E分别为AC1、BB1的中点.
|
（2）求二面角A1—DE—B1的大小.
22．（本小题满分14分）
设函数f(x)是定义在R上的函数，对任意实数m、n，都有
且当
（Ⅰ）证明（1）f(0)=1;（2）当
（3）
是R上的减函数；
（Ⅱ）如果对任意实数
、
恒成立，求实数a的取值范围.
寒假综合测试（一）数学答案
一、（1）B（2）A（3）D（4）A（5）A （6）C（7）B（8）A（9）C（10）B（11）D（12）C.
二、（13）12 （14）
（16）截面
，或截面
，或截面
.（注：未写截面二字不扣分）
三、（17）解：
………………………………………………………2分
当0<a<1
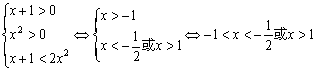……………………7分
当a>1时，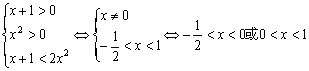
综上：当0<a<1时，不等式的解为
当a>1时，不等式的解为
…………………………12分
（18）解：（Ⅰ）由已知，易得A=2．
，解得
．
把（0，1）代入解析式
，得
．又
，解得
．
∴
为所求．…………………………………………………………6分
(Ⅱ)压缩后的函数解析式为
再平移，得
|
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
| 0 | 2 | 0 | -2 | 0 |
评分标准说明：
求出
、
、
各占2分．
列表与画图各占2分．……12分
（19）
（Ⅰ）解：由PD⊥平面ABCD，BC
平面ABCD，得PD⊥BC.
由AD⊥DC，AD∥BC，得BC⊥DC.
又
，则BC⊥平面PDC.………………………2分
所以∠BPC为直线PB与平面PDC所成的角
令PD=1，则DC=1，
，可求出PC=
.…………3分
由BC⊥平面PDC，
PDC，得BC⊥PC.
在Rt△PBC中，由PC=BC得∠BPC=45°
即直线PB与平面PDC所成的角为45°……………………4分
（Ⅱ）解法（一）：
|
平面PBC，
得平面PDC⊥平面PBC.
则DE⊥平面PBC.……………………………………5分
作
于F,连DF,由三垂线定理，得DF⊥PB.
则∠DFE为二面角D–PB–C的平面角…………7分
在Rt△PDC中，求得
|
.
在Rt△DEF中，
.
即二面角D–PB–C大小的正切值为………………8分
（20）解：（Ⅰ）设椭圆方程为
.由已知，
，由
解得a=3，
∴
为所求……………………………………………………3分
（Ⅱ）设直线l的方程为y=kx+b(k≠0)解方程组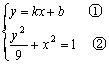
将①代入②并化简，得
……………………4分
Ⅰ由于k≠0
化简后，得
将④代入③化简后，得
.………………………………………9分
解得
∴
……………………………………………………………………10分
由已知，倾斜角不等于
∴l倾斜角的取值范围是
……………………………………12分
21.证：（1）取A1C1中点F，连DF，B1F1，DF平行且等于
AA1, ∴DF平行且等于EB1,
∴四边形DFB1E为平行四边形…………………（3分）∴DE∥B1F ∴DE∥平面A1B1C1………………（6分）（2）解：易知B1F⊥平面ACC1A1, ∵ED∥B1F, ED⊥平面ACC1A1，
∴ED⊥A1D1，ED⊥DF，∴∠A1DF即为所示二面角的平面角.………………9分由已知各棱长均为a，∴A1F=DF=
∴△A1DF为等腰直角三角形. ∴∠A1DF=45°∴所求二面角为45°……12分
22．（本小题满分14分） 解：（Ⅰ）（1）证明：在
中，令m=n=0, 得
……2分
若
时，有
这与题设矛盾
…………3分
（2）证明 ：当x>0时，－x<0，由已知得f(－x)>1…………4分
即
………………6分
（3）证明： 任取
………7分
在定义域R上为减函数………………10分
（Ⅱ）
是减函数，
恒成立，（i）当
时，a可取任意实数；…………11分
（i i）当
只需
…………12分（i i i）当
……13分
∴综上所述，满足题设要求的a的取值范围是
………………14分