高二年级教学质量检测数学试题卷
考生须知:
1. 本卷满分100分, 考试时间90分钟.
2. 答题前, 在答题卷密封区内填写学校、班级和姓名.
3. 所有答案必须写在答题卷上, 写在试题卷上无效.
4. 考试结束, 只需上交答题卷.
一.选择题 : 本大题共12小题, 每小题3分, 共36分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .
1. 若a>b,c ÎR,则下列命题中成立的是
(A)![]() . . (B)
. . (B)![]() .
(C)
.
(C) ![]() . (D)
. (D)![]() .
.
2. 双曲线![]() 的焦点坐标是
的焦点坐标是
(A)(-2,0),(2,0). (B)(0,-2),(0,2).
(C)(0,-4),(0,4). (D)(-4,0),(4,0).
3. 若2 + m 与m – 3 异号,则m的取值范围是
(A) m > 3. (B) –3< m < 3. (C) 2 < m < 3. (D) m< –2或– 3 < m < 2, 或m > 3.
4. 设直线2x – y –![]() = 0与y轴交于P点, 则点P将圆 ( x + 1 )
2 + y 2 = 25的直径分为两段的长度之比为
= 0与y轴交于P点, 则点P将圆 ( x + 1 )
2 + y 2 = 25的直径分为两段的长度之比为
(A)![]() 或
或![]() . (B)
. (B)![]() 或
或![]() .
(C)
.
(C)![]() 或
或![]() . (D)
. (D)![]() 或
或![]() .
.
5. 已知q Î[ – p,p], 则点P (1 , 1 )到直线 xcosq + ysinq = 2的最大距离为
(A) 2. (B)![]() .
(C)2 –
.
(C)2 –
![]() . (D) 2 +
. (D) 2 +![]() .
.
6. 已知实数对 ( x , y ) 满足x 2 + y 2 £ 1 且y ³ 0, 则y – x的取值范围是
(A) [ – 1 , 1 ] (B)[ 0 , 1] (C) [– 1 , ![]() ]
(D)[–
]
(D)[–![]() ,
,![]() ]
]
7.点P (0 , 1 )在直线ax + y – b = 0上的射影是点Q ( 1 , 0 ), 则a , b的值依次是
(A) –1 , 1 . (B) –1, –1. (C) 1 , 1. (D) 1, –1.
8. 抛物线的顶点在原点, 对称轴为坐标轴, 焦点是直线 3x + 5y – 15 = 0与y轴的交点, 那么抛物线的方程是
(A) x 2 = 12y . (B) y 2 = 10x . (C) y 2 = 20x . (D) x 2 = 6y.
9. 满足不等式![]() –
–![]() <
<![]() 的最小正整数x等于
的最小正整数x等于
(A)5. (B) 9 . (C) 24 . (D) 25.
10. 已知点F (![]() , 0 ), 直线l: x = –
, 0 ), 直线l: x = –![]() , 点B是l上的动点, 若过B垂直于y轴的直线与线段BF的垂直平分线交于点M, 则点M的轨迹是
, 点B是l上的动点, 若过B垂直于y轴的直线与线段BF的垂直平分线交于点M, 则点M的轨迹是
(A)双曲线. (B) 椭圆 . (C) 圆 . (D)抛物线.
11. 不论m , n为何实数, 方程x 2 + y 2 –2mx – 2ny + 4 ( m – n – 2 ) = 0所表示的曲线恒通过的定点坐标是
(A) (0 , 0) . (B) ( 2 , – 2 ) . (C) ( 2 , 2 ) . (D) ( 2 , – 2 )和 ( 2 , 2 ).
12. 已知A,B是椭圆![]() =1的左右两个顶点, 若椭圆上存在一点P, 且∠APB = 120°, ,是椭圆离心率e的取值范围是
=1的左右两个顶点, 若椭圆上存在一点P, 且∠APB = 120°, ,是椭圆离心率e的取值范围是
(A) [![]() , 1).
(B) (0,
, 1).
(B) (0, ![]() ].
(C) [
].
(C) [![]() , 1).
(D) [
, 1).
(D) [![]() ,
,![]() ].
].
二.填空题:本大题有5小题, 每小题4分, 共20分. 请将答案填写在答题卷中的横线上.
13.已知a>c>0,b>0,则![]() 与
与![]() 的大小关系是
.
的大小关系是
.
14. 购买每个4元的电器开关和每个6元的电器插头若干个, 但总费用不能超过24元,同时每一种电器至少要买一个,则不同的购买方法有 种.
15. 动圆C与定圆F 1: (x – 2) 2 + y 2 = 100内切, 与定圆F 2 : (x + 2) 2 + y 2 = 4 外切, 则动圆的圆心C的轨迹方程是 .
16. 已知曲线C1 : y = – x 2 + 4x – 2 , C2 : y 2 = x, 若C1、C2 关于直线l对称, 则l的方程是
17.若实数a,b,c同时满足下列条件:
(1) ![]() , (2)
, (2) ![]() , (3)
, (3) ![]() , (4)
, (4) ![]() .
.
则下列判断中正确的是 . (将正确判断的序号都填上)
(1) ![]() ; (2)
; (2) ![]() ; (3)
; (3)
![]() ; (4)
; (4) ![]() ; (5)
; (5)
![]() .
.
三.解答题:本大题有4小题, 共44分. 解答应写出文字说明, 证明过程或演算步骤.
18.(本小题满分10分)
某单位要建造一个长方体形状的无盖贮水池,其容积为
19. (本小题满分10分)
在△ABC中,内角B,C的平分线所在的直线方程分别为l 1: y + 1= 0, l2 : x + y + 1 = 0, A ( – 1 , – 4 ), 求BC边所在的直线方程.
20. (本小题满分10分)
当0 £ x < 1时不等式x 2 + kx > k – 1恒成立, 试求实数k的取值范围.
21. (本小题满分14分)
在O为原点的直角坐标系中,已知圆锥曲线的一个焦点为F ( 1 , 0 ), 对应这个焦点的准线方程为 x = – 1 , 且这条曲线经过点M ( 3 , 2![]() ).
).
(1)求此圆锥曲线的方程;
(2)已知圆锥曲线与直线 y = k (x – 4)相交于A、B两点, 求证: OA^
(3) 当△OAB的面积等于2![]() 时, 求k的值.
时, 求k的值.
22 附加题: (本题满分5分, 但全卷总分不超过100分)
已知a ³ 0 , b ³ 0, c ³ 0 , a + b + c =1, x = – a +2b +
(1) 求区域R 的面积;
(2) 设( x, y )为区域为R上的任意点;
1) 求x 2 + y 2 的最小值;
2) 求2x + y 的最大值.
高二年级教学质量检测
数学评分标准
一.选择题 : 本大题共12小题, 每小题3分, 共36分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | B | A | D | C | B | A | D | D | B | A |
二.填空题:本大题有5小题, 每小题4分, 共20分.
13.![]() <
<![]() 14. 8 15.
14. 8 15.![]() =1
16. x + y –2 = 0 17.(1) (4)(5)
=1
16. x + y –2 = 0 17.(1) (4)(5)
三.解答题:本大题有4小题, 共44分. 解答应写出文字说明, 证明过程或演算步骤.
18.(本小题满分10分)
解: 设水池底面一边的长度为x m,则另一边的长度为![]() m, 又设水池总造价为y元, 则
m, 又设水池总造价为y元, 则
y = 150´![]() + 120(6x +6´
+ 120(6x +6´![]() ) 4分
) 4分
= 240000 + 720(x + ![]() ) ³ 297600 3分
) ³ 297600 3分
当x = 40时, ymin = 297600元. 2分
答 当水池的底面是边长为
19. (本小题满分10分)
解: ∵l 1是∠B的平分线, ∴直线AB与BC关于l 1:对称 ,
∴点A关于l 1的对称点A1在直线BC上,
同理, 点A关于l 2的对称点A2 也在直线BC上, 3分
由对称定义求得A1( –1 , 2 ), A2( 3 , 0 ) , 6分
∴直线BC的方程为x + 2y – 3 = 0 1分
20. (本小题满分10分)
解1 设 f ( x ) = x 2 + kx – k + 1. 2分
要使0 £ x < 1时f ( x ) 恒为正,只需
![]() 或
或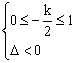 或
或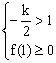 4分
4分
解得:0 < k < 1或–2 £ k £ 0或k < –2.
综上 k < 1. 4分
解2设 y = x2, y – 1 = – k ( x – 1 ), 4分
作抛物线y = x2及过定点P (1, –1)的直线y + 1 = – k ( x 1 ),
当0 £ x < 1时不等式恒成立等价于当0 £ x < 1时抛物线图象恒在直线上方
由kOA = –1,∴– k > –1,
解得k < 1. 6分
解3 化成k < ![]() ,
,
∵当 0 £ x < 1时,右边单调递增,
∵x = 0时,右边取最小值1, ∴k < 1.
21. (本小题满分14分)
解: (1) ∵ e =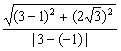 =1, ∴ 曲线是抛物线
=1, ∴ 曲线是抛物线
又∵F ( 1 , 0 ), 准线 x = – 1, ∴ 抛物线顶点在原点 p = 1– (– 1) = 2
∴ 所求的曲线方程为 y 2 = 4x 4分
|
|
(2)当k = 0时直线与抛物线仅一个交点, 不合题意,
∴ k ¹ 0由y = k ( x – 4 )得
x = ![]() +4 代入y 2
= 4 x 整理得: y 2 –
+4 代入y 2
= 4 x 整理得: y 2 –![]() y – 16 = 0
y – 16 = 0
设A (x 1 , y 1 ), B (
x 2 , y 2 ) 则y 1 + y 2 = ![]() , y 1y 2 = – 16
, y 1y 2 = – 16
∵A、B在y 2 = 4x上, ∴A (![]() , y 1
), B (
, y 1
), B (![]() , y 2
)
, y 2
)
(或由y = k(x – 4)代入得k2x2– 4(2k2 +1)x + 16k2 = 0, ∴x1x2 = 16 ).
∴ kOA·kOB =![]() =
=![]() =
=![]() = – 1, ∴ OA^OB.
5分
= – 1, ∴ OA^OB.
5分
(3) 设直线与x轴交于E, 则 E ( 4 , 0 ) ∴OE = 4
S△OAB =![]() OE( y
1 + y 2 ) =
OE( y
1 + y 2 ) =![]() ´4 y 1
– y 2 =2
´4 y 1
– y 2 =2![]() =2
=2![]() =2
=2![]()
解得k = ± 4 . 5分
|
|
22 附加题: (本题满分5分, 但全卷总分不超过100分)
解:∵ a ³ 0 , b ³ 0, c ³ 0 , a + b + c = 1, x = – a +2b +
∴ a = 1 – b – c ³ 0 ,
∴ x = –1 + 3b +
∴ ( x , y ) = ( – 1,2 ) + b ( 3, 4 ) + c(5, – 1) 且b ³ 0 , c ³ 0, 1 ³ b + c,
∴ ( x, y )表示由( 3, 4 ), ( 5, – 1)和( – 1,2 ) 所围的三角形区域(如右图所示).
∴ R 的面积为![]() .
3分
.
3分
∴x2 + y2的最小值即为原点到直线x + 5y – 9 = 0的距离的平方, 为![]() .
.
而x = 2, y = 6时,2x + y 取最大值为10 . 2分