高二上学期数学竞赛

高二上学期数学竞赛

一、选择题（每小题6分,满分30分）

2. 设a, bÎR, ab≠0，那么，直线 ax-y+b=0和曲线 bx²+ay²=ab 的图形是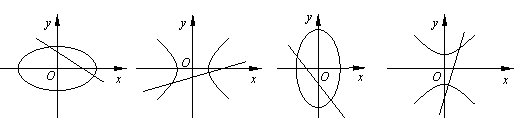
　　　 (A)　　　　　　　　 (B)　　　　　　　 (C)　　　　　　　 (D)

2. 一个圆的圆心为椭圆的右焦点，且该圆过椭圆的中心交椭圆于P,直线PF（F为椭圆的左焦点）是该圆的切线，则椭圆的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　 A．　　　　　　　　　　　　B．　　　　　　　　　　　　　C．　　　　　　　　　　　 D．　　

3.　当时，方程的解的个数是　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　 A．0　　　　　　　　　　　　　B．1　　　　　　　　　　　　　　　 C．2　　　　　　　　　　　　　　D．3

4. 若xÎ[-,-]，则y= tan(x+)-tan(x+)+cos(x+)的最大值是
(A)　　 (B) 　　　(C)　 　 (D)

5．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足　　　　　　　　

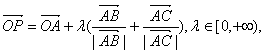　 则P的轨迹一定通过△ABC的　　　　 （　　）

　　　 A．外心　　　　　　　　　 B．内心　　　　　　　　　 C．重心　　　　　　　　　 D．垂心

　二.填空题(每小题8分,满分40分)

6.  不等式x³-2x²-4x+3＜0的解集是__________

7.　　　 设F₁,F₂是椭圆的两个焦点，P是椭圆上的点，且PF₁:PF₂=2:1，则△PF₁F₂的面积等于. __________

8.　　　 已知A={xx²-4x+3＜0,xÎR}, B={xx²-2(a+7)x+5≤0,xÎR}．若AÍB, 则实数a的取值范围是____________.

9.　　　 若方程2a·9^sinx +4a·3^sinx +a – 8=0有解，则a的取值范围是________.

10. 已知x,y都在区间(-2,2)内，且xy＝-1，则函数u=+的最小值是________.

三.解答题(满分50分)

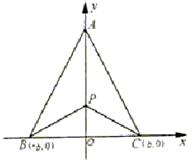
1. （本题满分10分）有三个城镇，分别位于A，B，C三点处，且AB=AC=a，BC=2b.今计划合建一个中心院，为同时方便三镇，准备建在BC的垂直平分线上的P点处，（建立坐标系如图）若希望点P到三镇距离的平方和为最小，点P应位于何处？

　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2. （本题满分10分）已知a,b,c∈R，函数f(x)= ax²+bx+c.

（1）若a+c=0，f(x)在[-1,1]上的最大值为2，最小值为，证明：a0且<2；

（2）若a>0，p、q满足p+q=1，且对任意的实数x、y均有pf(x)+qf(y)≥f(px+qy)，

证明：0≤p≤1.

3.　　 （本题满分15分） 已知直线与圆相切于点T，且与双曲线相交于A、B两点.若T是线段AB的中点，求直线的方程.

 

4．（本题满分15分）已知常数a>0，向量c=（0，a），i=（1，0），经过原点O以c+λi为方向向量的直线与经过定点A（0，a）以i－2λc为方向向量的直线相交于点P，其中λ∈R.试问：是否存在两个定点E、F，使得PE+PF为定值.若存在，求出E、F的坐标；若不存在，说明理由.

高二数学竞赛答案

1—5  BDDCB。6.（-3， ）U（ ， 3）.　7. 4.　 8. [-4, ∞

9.[ 8/31, 72/23 ]　10. 12/5

11.本小题主要考查函数，不等式等基本知识，考查运用数学知识分析问题和解决问题的能力.满分10分.

　　解：由题设可知，记设P的坐标为（0，），则P至三镇距离的平方和为　所以，当时，函数取得最小值.  答:点P的坐标是

12. 分析：（1）用反证法。假设a=0或≥2，由a+c=0，得a=-c，故f(x)= ax²+bx- a.

　　当a=0时，f(x)= bx，是一个单调函数，其最大值为b，最小值为-b，又已知得：b=2且-b=，矛盾，故a0。

当≥2时，-≥1，函数f(x)在[-1,1]上也是单调函数，由上可知矛盾，故<2。

综合以上两种情况，得a0且<2；

(2)pf(x)+qf(y)-f(px+qy)=p(ax²+bx+c)+q(ay²+by+c)-[a(px+qy)²+b(px+qy)+c]

=ap(1-p)²x²-2apqxy+aq(1-q)y²=apq(x-y)²≥0,因为a>0,(x-y)²≥0，所以pq≥0,p(1-p)≥0，故0≤p≤1.

13. 直线与轴不平行，设的方程为  代入双曲线方程 整理得

　……………………2分　 而，于是

　从而 即 ……6分

点T在圆上　 　即　　　 ①

由圆心　.　得 　　　则 　或

当时，由①得 的方程为 ；

当时，由①得  的方程为.故所求直线的方程为 或 …………………………15分

14.本小题主要考查平面向量的概念和计算，求轨迹的方法，椭圆的方程和性质，利用方程判定曲线的性质，曲线与方程的关系等解析几何的基本思想和综合解题能力，满分14分。

　　解：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到两定点距离的和为定值.

　　∵i=(1,0),c=(0,a),　∴

　　因此，直线OP和AP的方程分别为　y=ax和y－a=－2ax .

　　消去参数，得点P（x,y）的坐标满足方程y (y－a)=－2a²x² ,

　　整理得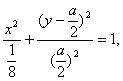　　　　　　　　  ①

　　因为a>0，所以得：

　 （i）当a=时，方程①是圆方程，故不存在合乎题意的定点E和F；

　 （ii）当0<a<时，方程①表示椭圆，焦点E和

　　　　为合乎题意的两个定点；

  （iii）当a>时，方程①表示椭圆，焦点E和F））为合乎题意的两个定点.