高二数学第八章知识总结

	学科：数学
	教学内容：高二数学第八章知识总结

一、本章在第一章直线方程的基础上，研究了直角坐标系中曲线和方程之间的对应关系，然后根据所求曲线的定义，得出了几种圆锥曲线的方程，并通过方程讨论了圆、椭圆、双曲线和抛物线的性质及应用.

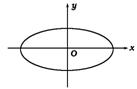
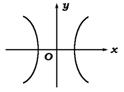
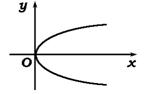
二、由椭圆、双曲线、抛物线的几何条件求其标准方程，并通过分析标准方程研究这三种曲线的几何性质.三种曲线的标准方程(各取其中一种)和图形、性质如下表：

	椭圆	双曲线	抛物线
几何 条件	与两个定点的距离和等于常数	与两个定点的距离差的绝对值等于常数	与一个定点和一条定直线的距离相等
标准 方程	+＝1(a>b>0)	-＝1(a>0,b>0)	y2＝2px(p>0)
图形
顶点 坐标	(±a,0),(0,±b)	(±a,0)	(0,0)
对称轴	x轴，长轴长2a y轴，短轴长2b	x轴，实轴长2a y轴，虚轴长2b	x轴
焦点 坐标	(±c,0)c＝	(±c,0)c＝	(,0)
离心率 (e＝)	0<e<1	e>1	e＝1
准线	x＝±	x＝±	x＝-
渐近线		y＝±x

三、圆、椭圆、双曲线、抛物线的统一性

(1)从方程的形式看，在直角坐标系中，这几种曲线的方程都是二元一次的，所以称它们为二次曲线.

(2)除圆以外，从点的集合(或轨迹)的观点来看：它们都是与定点和定直线距离的比是常数e的点的集合(或轨迹)，这个定点是它们的焦点，定直线是它们的准线，只是由于离心率e的不同，而分为椭圆，双曲线和抛物线三种曲线.

(3)从天体运的轨道看：天体运动的轨道是这四种曲线，例如，人造卫星、行星、彗星等由于运动的速度的不同，它们的轨道是圆、椭圆、抛物线或双曲线.

(4)四种曲线又可以看作不同的平面截圆锥面所得到的截线，因此它们又统称圆锥曲线.

四、本章中应注意运用和掌握的数学思想方法

(1)数形结合思想

(2)转化的思想

(3)待定系数法、配方法、分析法等.