高二数学第八章综合测试题A
一、选择题(5分×12＝60分)
1.已知椭圆
+
＝1的点P到左准线之距为
，则P到右准线之距为( )
A.8 B.
C.
D.
2.抛物线y＝4ax2(a＜0＝的焦点坐标是( )
A.(a,0) B.(
,0) C.(0,
) D.(0,- )
3.过双曲线的一个焦点F1的弦为PQ，另一焦点F2，若PQ垂直于实轴，且∠PF2Q＝90°，则其离心率为( )
A. 
+1 B. C.
-1 D.
+1
4.已知双曲线的两条渐近线方程是y＝±
x，焦点坐标是(±
，0)，那么它的两准线间的距离是( )
A.
B. 
C.
D.
5.一动圆与两圆x2+y2＝1和x2+y2-x+12＝0都外切，则动圆圆心的轨迹为( )
A.抛物线 B.椭圆
C.双曲线的左支 D.双曲线的右支
6.已知方程x2sinα-y2cosα＝1(0≤α≤2π)表示焦点在y轴上的椭圆，则α的取值范围是( )
A.( 
，
) B.(
，π)
C.( 
，) D.(
，)
7.过抛物线y＝ax2(a＞0)的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别是p、q，则
+
＝( )
A
C
8.已知p1(x1,y1)、p2(x2,y2)是抛物线y＝2px(p＞0)上不同的两点，则x1x2＝
是直线p1p2通过抛物线焦点F的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
9.设过双曲线右焦点的弦为AB，则以AB为直径的圆与双曲线的右准线的位置关系是( )
A.相交 B.相似 C.相离 D.不能确定
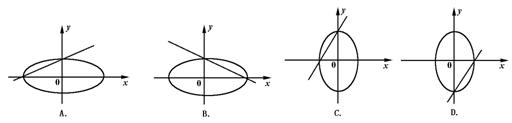
10.方程y＝ax+b和a2x2+y2＝b2(a＞b＞1)在同一坐标系中的图形可能是( )
11.点(m,n)在双曲线
-y2＝1上运动，则点(m+1,2n)运动的轨迹方程为( )
A. 
-4y2＝1 B.x2-y2＝4
C. 
-4y2＝1 D.
-y2＝1
12.设抛物线y2＝2px(p≠0)与椭圆ax2+by2＝1(a＞b＞0)的离心率之比为λ1，双曲线ax2-by2＝1上一点到右准线与右焦点距离之比为λ2，则
的取值( )
A.小于1 B.等于1
C.大于1 D.与1的大小关系不能确定
二、填空题(4分×4＝16分)
13.已知椭圆的中心在原点，焦点F1、F2在y轴上，P点在椭圆上运动，若｜PF1｜·｜PF2｜的最大值为16，最小值为7，则其标准方程为 .
14.点P(-3，0)是圆x2+y2-6x-55＝0内一定点，动圆M与已知圆相内切且过P点，则圆心M的轨迹方程为 .
15.已知A(3，2)，若抛物线y2＝2px(p＞0)上的点到焦点F的距离与到A点的距离之和的最小值为5，则抛物线的方程为 .
16.等轴双曲线上有一点P到中心的距离为d.则点P到两焦点的距离之积为 .
三、解答题(共74分)
17.已知椭圆+y2＝1的焦点为F1和F2，抛物线的顶点在原点，且开口向右，A为两条曲线的一个公共点，若∠F1AF2＝60°，求此抛物线的方程.
18.双曲线的中心在坐标原点O，焦点在x轴上，过双曲线右焦点且斜率为
的直线交双曲线于P、Q两点，若OP⊥OQ，｜PQ｜＝4，求双曲线方程.
19.已知圆x2+y2-2y-8＝0的内接正方形ABCD，若顶点A、B在斜率为1的一条直线l上，C、D在中心为原点，且长轴在x轴上的一个椭圆上，求原椭圆的方程.
20.已知抛物线C顶点在原点，准线方程y＝-
，将抛物线C绕y轴旋转一周所生成的曲面作为一容器的内侧面，在容器底放一小气球，随着向球内注入的空气的增加(假定气球保持球状)球半径r逐渐增大.试问：当r增大到怎样时，气球便离开容器的底部?说明道理.
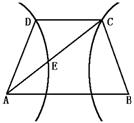
21.如图，已知梯形ABCD中｜AB｜＝2｜CD｜，点E分有向线段
所成的比为λ，双曲线过C，D，E三点，且以A、B为焦点，当
≤λ≤
时，求双曲线离心率e的取值范围.
22.已知抛物线y2＝2x，直线l:y＝x-4，是否存在矩形ABCD，它的一条对角线AC在直线l上，顶点B、D在已知抛物线上，且AC与BD的夹角为arctan3.若存在，求出这个矩形的面积，若不存在，说明理由.
参考答案
第八章综合测试题A
一、1.A 2.C 3.A 4.C 5.C 6.D 7.C 8.B 9.A 10.C 11.B 12.C
二、13.y＝±
14. 
+
＝1 15.y2＝8x 16.d2
三、17.y2＝
x
18.x2-
＝1
19. 
+
＝1
20.r＞
时，气球离开容器底部上升.
21.e∈［
，
］
22.存在 S△＝