高二数学第八章综合测试题B

高二数学第八章综合测试题B

 

一、选择题(5分×12＝60分)

1.已知椭圆的中心在原点，焦点在x轴上，且长轴长为12，离心率为，则椭圆的方程是(　　)

A.  +=1　　　　　　　　 B. +=1

C. +=1　　　　　　　　　 D. +=1

2.双曲线-=1的两条渐近线互相垂直，那么的离心率为(　　)

A.2　　　　　　 B. 　　　　　C. 　　　　 D.

3.椭圆的两个焦点三等分它的准线间的距离，则它的离心率是(　　)

A. 　　　　 B. 　　　　 C. 　　　　 D.

4.动圆C经过定点F(0，2)且与直线y+2=0相切，则动圆的圆心C的轨迹方程是(　　)

A.x²=8y　　　　 B.y²=8x　　　　 C.y=2　　　　　 D.x=2

5.已椭圆+=1(a＞b＞0)的离心率为，若将这个椭圆绕它的右焦点按逆时针方向旋转后，所得椭圆的一条准线的方程是y=,则原来椭圆的方程是(　　)

A. +=1　　　　　　　　　B. +=1

C. +=1　　　　　　　　　 D. +=1

6.经过点M(2，-2)且与双曲线-=1有共同渐近线的双曲线方程是(　　)

A. -=1　　　　　　　 B. -=1

C. -=1　　　　　　　 D. -=1

7.抛物线y²=x关于直线x-y=0对称的抛物线的焦点坐标为(　　)

A.(1，0)　　　　　　B.(0，1)　　　　　　C.(0，)　　　D.( ，0)

8.若点A的坐标是(3，2)，F是抛物线y²=2x的焦点，点P在抛物线上移动，为使得｜PA｜+｜PF｜取得最小值，则P点的坐标是(　　)

A.(1，2)　　　　　　B.(2，1)　　　　　　C.(2，2)　　　　　　D.(0，1)

9.AB是抛物线x=y²的一条焦点弦，且｜AB｜=4，则AB的中点到直线x+1=0的距离为(　　)

A. 　　　　　 B.2　　　　　　 C.3　　　　　　 D.

10.过点(0，3)作直线l，如果它与双曲线-=1只有一个公共点，则直线l的条数为(　　)

A.1　　　　　　 B.2　　　　　　 C.3　　　　　　 D.4

11.已知点A(1，2)，过点(5，-2)的直线与抛物线y²=4x交于另外两点B、C，那么△ABC是(　　)

A.锐角三角形　　　　　　　　　　　　B.钝角三角形

C.直角三角形　　　　　　　　　　　　D.不确定

12.P为双曲线C上一点，F₁、F₂是双曲线C的两个焦点，过双曲线C的一个焦点作∠F₁PF₂的平分线的垂线，设垂足为Q，则Q点的轨迹是(　　)

A.直线　　　　　B.圆　　　　　　　　C.椭圆　　　　　D.双曲线

二、填空题(4分×4＝16分)

13.已知双曲线-=1上点P到右焦点的距离为8，则点P到左准线的距离为　　　　　  .

14.椭圆+y²=1关于直线y=x-3对称的椭圆的方程是　　　　　  .

15.P是抛物线y²=x上的动点，Q是圆(x-3)²+y²=1的动点，则｜PQ｜的最小值为　　　　　  .

16.有下列命题

(1)到定直线x=和定点F(c,0)的距离之比为(a＞c＞0)的点的轨迹是椭圆.

(2)到定点F(-c，0)和定直线x=-的距离之比为(a＞c＞0)的点的轨迹是椭圆.

(3)到定点F(c,0)和定直线x=的距离之比为

(c＞a＞0)的点的轨迹是双曲线右半支

(4)到定直线x=-和定点F(-c,0)的距离之比为(c＞a＞0)的点的轨迹是双曲线

其中正确命题的序号是　　　　　  .

三、解答题(共74分)

17.已知直线l交椭圆+=1于M、N两点，B(0，4)是椭圆的一个顶点，若△BMN的重心恰是椭圆的右焦点，求直线l的方程.

 

 

 

 

 

18.正方形的一条边AB在直线y=x+4上，顶点C、D在抛物线y²=x上，求正方形的边长.

 

 

 

 

19.已知椭圆+=1(a＞b＞0)的右焦点F，经过F作倾角为135°的直线l交椭圆于A、B两点，线段AB的中点为M，直线AB与OM的夹角为θ，且tanθ=3,求这个椭圆离心率的值.

 

 

 

 

 

20.已知双曲线-=1的左、右焦点分别是F₁、F₂，左准线为l，能否在双曲线的左支上求一点P，使｜PF₁｜是P到l的距离d与｜PF₂｜的等比中项?若能，求出P点坐标，若不能，说明理由.

 

 

 

 

 

21.若椭圆x²+4(y-a)²=4与抛物线x²=2y有公共点，求实数a的取值范围.

 

 

 

 

 

22.已知直线l:x=-1,点F(1，0)，以F为焦点，l为相应的准线的椭圆短轴的一顶点为B，P为FB的中点.

(1)求P点的轨迹方程，并说明它是什么曲线；

(2)M(m,0)为定点，求｜PM｜的最小值.

 

 

 

 

 

 

 

参考答案

第八章综合测试题B

1.D　2.C  3.B　4.A　5.C  6.C　7.C　8.C  9.D　10.D　11.C　12.B

13.8或　14.(x-3)²+=1　15. -1　16.②

17.解：椭圆的右焦点为F(2，0)，设M(x₁,y₁),N(x₂,y₂)则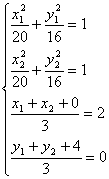

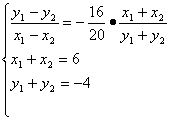　∴k_MN==，又l过MN的中点(3，-2)，∴l的方程为y=(x-3)-2.即6x-5y-28=0.

18.解：设CD的方程为y=x+b,由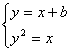消去x得y²-y+b=0，设C(x₁,y₁),D(x₂,y₂),则y₁+y₂=1,y₁y₂=b,∴｜CD｜==，又AB与CD的距离d=,由ABCD为正方形有=,解得b=-2或b=-6.∴正方形的边长为3或5).

19.解：设A(x₁,y₁),B(x₂,y₂),AB中点为M(x₀,y₀),则+=1, +=1,两式相减可得k_AB==-=-=-1,∴a²y₀=b²x₀.又k_OM===1-e²，而｜｜=tanθ=3,∴k_OM=或k_OM=2(∵a＞b，＜1，舍去，∴1-e²=，即离心率e=.

20.解：假设存在P点在双曲线的左支上，使得｜PF₁｜是P到l的距离d与｜PF₂｜的等比中项，则｜PF₁｜²=d｜PF₂｜，由双曲线方程可知：a=5,b=12,c=13,且｜PF₁｜=de=d，∵点P在双曲线左支上，∴｜PF₂｜=｜PF₁｜+2a=+10,∴()²=d(+10),解得d=,左顶点到左准线l的距离d_min=5-=＞矛盾，故不存在满足题设的点P.

21.解：令x=2cosθ,y=a+sinθ,θ∈［0,2π］代入抛物线当程，得4cos²θ=2(a+sinθ)，∴a=2cos²θ-sinθ=2-2sin²θ-sinθ=-2(sinθ+)+,∵-1≤sinθ≤1,∴-1≤a≤，即实数a的取值范围为［-1, ］

22.解：(1)设P点坐标为(x,y)，则B点坐坐为(2x-1,2y).依题意有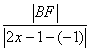==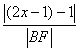e，即　(2x-2)²+4y²=2x(2x-2),∴y²=x-1(x＞1)，故P点的轨迹是以(1，0)为顶点，x轴为对称轴，开口向右的抛物线(不含顶点).

(2)｜PM｜===(x＞1)，当＞1，即m＞时，｜PM｜_min=，当≤1,即m≤时，｜PM｜无最小值.