高二数学第二学期教学质量检测试卷3
| 题号 | 1-10 | 11-14 | 15 | 16 | 17 | 18 | 总分 |
| 得分 |
注：可以使用计算器；本试卷满分100分，在90分钟内完成
【参考公式】
 |
一、选择题：（本大题共10小题，每小题4分，共40分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
每题给出4个答案，其中只有一个是正确的，请把选出的答案编号填在上面的答题表中，否则不给分.
1、用α表示一个平面，l表示一条直线，则平面α内至少有一条直线与l
A、平行 B、相交 C、异面 D、垂直
2、下列图形一定是平面图形的是
A、四边相等的四边形 B、四条线段首尾顺次连结而成的四边形
C、两对角线相交的四边形 D、两组对角分别相等的四边形
3、过正方形ABCD的顶点A作线段AP⊥平面ABCD，且AP=AB，则平面ABP与平面CDP所成的二面角的度数是
A、30º B、45º C、60º D、90º
4、体积为9的斜三棱柱ABC-A1B
A、
B、
5、已知
，
，则
与
的数量积等于
A、-15 B、
6、若S = (x-1)4 + 4(x-1)3 + 6(x-1)2 + 4(x-1) + 1，则S化简后得
A、x4 B、(x-2)
7、从A地到B地有3种走法，从B地到C地有2种走法，从A地不经过B地到C地有4种走法，则从A地到C地的不同走法有
A、9种 B、10种 C、14种 D、24种
8、周末小明去广州的概率为
，小华去广州的概率是
，假定两人的行动相互之间没有影响，则周末小明、小华至少有一人去广州的概率为
A、
B、 C、
D、
9、两个事件为对立事件是这两个事件互斥的
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、不充分不必要条件
10、抛两个各面分别标有1，2，3，4，5，6的均匀的骰子，“向上的两个数之和为
A、
B、
C、
D、
二、填空题：（本大题共4小题，每小题4分，共16分）
11、已知
=（0，-1，1），
=（1，2，-1），则与的夹角等于______度.
12、如果两个球的表面积之比是4：1，那么这两个球的体积之比是 .
13、甲、乙二人参加有奖知识竞赛，共有10个不同的题目，其中选择题6个，判断题4 个．甲、乙二人依次各抽一题．甲抽到选择题、乙抽到判断题的种数为______种.
14、小明通过英语四级测试的概率为
，他连续测试3次，那么其中恰有一次获得通过的概率是________.
三、解答题：（第15、16题每题12分，第17、18题每题10分，共44分）.
15、有6名同学站成一排，求：
（1）甲不站排头也不站排尾有多少种不同的排法.
（2）甲不站排头，且乙不站排尾有多少种不同的排法.
（3）甲、乙、丙不相邻有多少种不同的排法.
解：
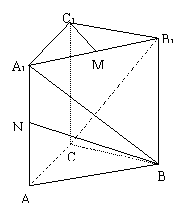16、如图，直三棱柱ABC-A1B
（1）求
的长；
（2）求cos<
,
>的值；
（3）求证：A1B⊥C
17、已知
展开式中第三项的系数比第二项的系数大162，求：
（1）n的值；
（2）展开式中含x3的项.
解：
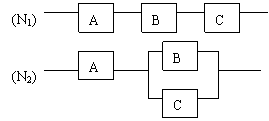
18、如图，用A、B、C三类不同的元件连接成两个系统N1、N2，当元件A、B、C都正常工作时，系统N1正常工作；当元件A正常工作且元件B、C至少有一个正常工作时，系统N2正常工作，已知元件A、B、C正常工作的概率依次为0.80，0.90，0.90，分别求系统N1、N2正常工作的概率P1、P2.
解：
参考答案
一、选择题：（本大题共10小题，每小题4分，共40分）
DCBBA ABCAD
二、填空题：（本大题共4小题，每小题4分，共16分）
11、150º
12、8：1
13、
（或24） 14、
三、解答题：（第15、16题每题12分，第17、18题每题10分，共44分）.
15、解：（1）
种；…………………………………………………4分
（2）
种； …………………………………………4分
或
（甲在尾）+ 
（甲不在尾）=120+384=504；
或
（3）
种
…………………………………………4分
16、解：（1）以射线
、
、
分别为坐标系OX、OY、OZ轴，
则B（0，1，0），N（1，0，1），……………………………………………2分
=
=
…………………………2分
（2）A1（1，0，2），B1（0，1，2），C（0，0，0）
（1，-1，2），
（0，1，2），
………………………2分
∴cos<
，
>=
=
=
…2分
（3）C1（0，0，2），M（
，，2），
=（，，0），
（-1，1，-2） …………………2分
∴·=×（-1）+×1+0×（-2）=0
A1B⊥C
17、解：（1）∵
2分
依题意得
∴
……………………………2分
………………………………1分
（2）设第r +1项含x3项，
则
……………………………2分
…………………………………1分
∴第二项为含x3的项：T2=-2
=-18x3 ………………………………2分
18、解：分别记元件A、B、C正常工作的事件A、B、C， …………1分
由题设得：
P1 =P（A·B·C）= P（A）·P（B）·P（C） …………………………2分
= 0.8×0.9×0.9=0.648
∴系统N1正常工作的概率为0.648 ……………………………2分
P2 = P（A）·[1－P（
………………………2分
= 0.80×(1－0.10×0.10) = 0.80×0.99 = 0.792 ………………………2分
∴系统N2正常工作的概率为0.792. ……………………………………1分