专题十 圆锥曲线练习
跟踪练习
一、选择题
1.到定点的距离与到定直线的距离之比等于log23的点的轨迹是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
2.椭圆x2+5y2-4x+10y+4=0的准线方程是( )
A.x=±![]() B.x= -
B.x= -![]() ,x=
,x=![]()
C.x= -![]() ,x=
,x=![]() D.x= -
D.x= -![]() ,x=
,x=![]()
3.双曲线![]() -
-![]() =1的渐近线方程是( )
=1的渐近线方程是( )
A.y=±2x B.y=±![]() x C.y=±2(x-1) D.y=±
x C.y=±2(x-1) D.y=±![]() (x-1)
(x-1)
4.以原点为顶点,椭圆C:![]() +
+![]() =1的左准线为准线的抛物线交椭圆C的右准线于A、B两点,则AB等于( )
=1的左准线为准线的抛物线交椭圆C的右准线于A、B两点,则AB等于( )
A.2 B.
5.方程y2=ax+b与y=ax+b(a≠0)表示的图形可能是( )
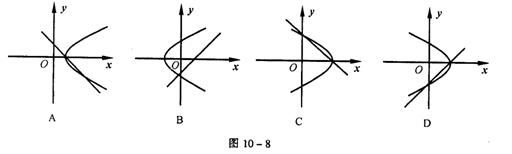
6.中心在原点,焦点坐标为(0,
±5![]() )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为![]() ,则椭圆方程为( )
,则椭圆方程为( )
A.![]() +
+![]() =1 B.
=1 B.![]() +
+![]() =1
=1
C.![]() +
+![]() =1 D.
=1 D.![]() +
+![]() =1
=1
7.抛物线y2=2px与y2=2q(x+h)有共同的焦点,则p、q、h之间的关系是( )
A.2h=q-p B.p=q+2h C.q>p>h D.p>q>h
8.过定点P(0,2)作直线l,使l与曲线y2=4(x-1)有且仅有1个公共点,这样的直线l共有( )
A.1条 B.2条 C.3条 D.4条
9.已知方程![]() +
+![]() =1表示焦点在y轴上的椭圆,则m的取值范围是( )
=1表示焦点在y轴上的椭圆,则m的取值范围是( )
A.m<2 B.1<m<2
C.m<-1或1<m<2 D.m<-1或1<m<![]()
10.过椭圆![]() +
+![]() =1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是( )
=1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是( )
A.ab B.ac C.bc D.b2
11.将曲线C向右平移3个单位,再向下平移1个单位得到曲线C′,若曲线C′的方程为![]() -
-![]() =1,则曲线C的焦点坐标为( )
=1,则曲线C的焦点坐标为( )
A.(6,-1)(0,-1) B.(-6,1),(0,1) C.(-3,2)(-3,-4) D.(3,2)(3,-4)
12.已知双曲线![]() -
-![]() =1和椭圆
=1和椭圆![]() +
+![]() =1(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边长的三角形是( )
=1(a>0,m>b>0)的离心率互为倒数,那么以a、b、m为边长的三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.锐角或钝角三角形
二、填空题
13.圆锥曲线![]() 的焦点坐标是
。
的焦点坐标是
。
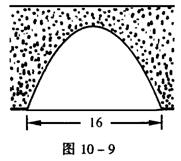
14.某桥的桥洞呈抛物线形(如图10-9),桥下水面宽16米,当水面上涨2米后达到警戒水位,水面宽变为12米,此时桥洞顶部距水面高度约为 米(精确到0.1米)
15.椭圆![]() +
+![]() =1的一个焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是
。
=1的一个焦点为F1,点P在椭圆上,如果线段PF1的中点M在y轴上,那么点M的纵坐标是
。
16.已知椭圆![]() +
+![]() =1与双曲线
=1与双曲线![]() -
-![]() =1(m,n,p,q∈{xx是正实数集})有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则PF1·PF2= 。
=1(m,n,p,q∈{xx是正实数集})有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则PF1·PF2= 。
三、解答题
17.已知椭圆C的焦点分别为F1(-2![]() ,0)和F2(2
,0)和F2(2![]() ,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点,求线段AB的中点坐标。
,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点,求线段AB的中点坐标。
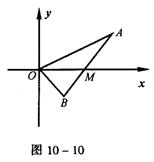
18.如图10-10,线段AB过x轴正半轴上一定点M(m,0),端点A、B到x轴的距离之积为2m,以x轴为对称轴,过A、O、B三点作抛物线,求该抛物线的方程。
19.把椭圆(x-1)2+![]() =1绕它的中心旋转90°后再沿x轴方向平行移动,使变换后的椭圆截直线y=
=1绕它的中心旋转90°后再沿x轴方向平行移动,使变换后的椭圆截直线y=![]() x所得的线段长为
x所得的线段长为![]() ,试写出变换后的椭圆方程。
,试写出变换后的椭圆方程。
20.已知椭圆的两个焦点分别为F1(0,-2![]() ),F2(0,2
),F2(0,2![]() ),离心率e=
),离心率e=![]() 。
。
(1)求椭圆方程;
(2)一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N,且线段MN中点的横坐标为-![]() ,求直线l倾斜角的取值范围。
,求直线l倾斜角的取值范围。
21.椭圆中心是坐标原点O,焦点在x轴上,e=![]() ,过椭圆械焦点F的直线交椭圆于P、Q两点,PQ=
,过椭圆械焦点F的直线交椭圆于P、Q两点,PQ=![]() 且OP⊥OQ,求此椭圆的方程。
且OP⊥OQ,求此椭圆的方程。
22.已知圆C1的方程为(x-2)2+(y-1)2=![]() ,椭圆C2的方程为
,椭圆C2的方程为![]() +
+![]() =1(a>b>0),C2的离心率为
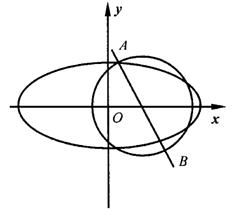
=1(a>b>0),C2的离心率为![]() ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程。
参考答案
1.C 2.B 3.D 4.D 5.C 6.C 7.A 8.C 9.D 10.C 11.B 12.B
13.(-4,0) (6,0) 14.2.6 15. ±![]() 16.m-p
16.m-p
17.[解] 设椭圆C的方程为![]() +
+![]() =1,
=1,
由题意a=3,c=2![]() ,于是b=1。
,于是b=1。
∴椭圆C的方程为![]() +y2=1。
+y2=1。
由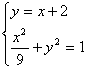 得10x2+36x+27=0
得10x2+36x+27=0
因为该二次方程的判别式△>0,所以直线与椭圆有两个不同交点。
设A(x1,y1),B(x2,y2)
则x1+x2= -![]() ,
,
故线段AB的中点坐标为(-![]() ,
,![]() )。
)。
18.[解] 设所求抛物线方程为 y2=2px(p>0) ①
若AB不垂直于x轴,设直线AB方程为:y=k(x-m)(k≠0) ②
由①,②消去x,得y2-![]() y-2pm=0 ③
y-2pm=0 ③
设A、B的坐标分别为A(![]() ,a),B(
,a),B(![]() ,b)。
,b)。
则a,b是方程③的两个根。
∴ab= -2pm,
又a·b=2m,即ab=-2m,
由-2pm= -2m(m>0)得p=1,
则所求抛物线方程为y2=2x。
若AB垂直于x轴,直线AB的方程为x=m,A、B两点关于x轴对称,
故m2=2pm,2m=2pm,
又m≠0,∴p=1。
则所求抛物线方程为y2=2x。
综上,所求抛物线方程为y2=2x。
19.[解] 旋转后的椭圆方程为(y-1)2+![]() =1。
=1。
设平移后的椭圆方程为(y-1)2+![]() =1。
=1。
解方程组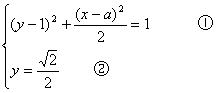
将②代入①后,得(![]() x-1)2+
x-1)2+![]() =1。化简后,得2x2-2(a+
=1。化简后,得2x2-2(a+![]() )x+a2=0 ③
)x+a2=0 ③
由椭圆截直线所得线段长为![]() 有
有![]() ·
·![]() =
=![]()
解得a=0或a=2![]() ,并且都使方程③有实根。
,并且都使方程③有实根。
∴变换后的椭圆方程为:![]() +(y-1)2=1
+(y-1)2=1
或![]() +(y-1)2=1。
+(y-1)2=1。
20.[解] (1)设椭圆方程为![]() +
+![]() =1。由已知,c=2
=1。由已知,c=2![]() ,由e=
,由e=![]() 解得a=3,∴b=1。∴
解得a=3,∴b=1。∴![]() +x2=1为所求椭圆方程。
+x2=1为所求椭圆方程。
(2)设直线l的方程为y=kx+b(k≠0)
解方程组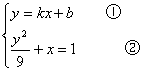
将①代入②并化简,得(k2+9)x2+2kbx+b2-9=0。
∴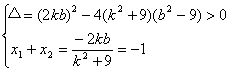 由于k≠0
由于k≠0
则化简后,得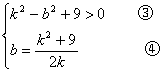
将④代入③化简后,得k4+6k2-27>0
解得k2>3
∴k< -![]() 或k>
或k>![]()
由已知,倾斜角不等于![]() ,
,
∴l倾斜角的取值范围是(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() )。
)。
21.[解] ![]() +
+![]() =1,(a>b>0)
=1,(a>b>0)
当PQ⊥x轴时,F(-c,0),
FP=![]() ,又FQ=FP且OP⊥OQ,∴OF=FP。
,又FQ=FP且OP⊥OQ,∴OF=FP。
即c=![]() ∴ac=a2-b2,
∴ac=a2-b2,
∴e2+e-1=0 ∴e=![]() 与题设e=
与题设e=![]() 不符。所以PQ不垂直x轴。
不符。所以PQ不垂直x轴。
设PQ∶y=k(x+c),P(x1,y1),Q(x2,y2),
∵e=![]() ∴a2=
∴a2=![]() c2,b2=
c2,b2=![]() c2,
c2,
所以椭圆方程可化为:3x2+12y2-4c2=0。
将PQ方程代入,得(3+12k2)x2+24k2cx+12k2c2-4c2=0
x1+x2=![]() ,x1x2=
,x1x2=![]()
由PQ=![]() 得
得![]() ·
·![]() =
=![]() ①
①
∵OP⊥OQ ∴![]() ·
·![]() = -1即x1x2+y1y2=0,
= -1即x1x2+y1y2=0,
∴(1+k2)x1x2+k2c(x1+x2)+c2k2=0 ②
解②得k2=![]() 代入①解得c2=3
代入①解得c2=3
∴a2=4,b2=1,则所求椭圆方程为![]() +y2=1。
+y2=1。
22.[解] 由e=![]() ,得
,得![]() =
=![]() ,a2=2c2,b2=c2。
,a2=2c2,b2=c2。
设椭圆方程为![]() +
+![]() =1。
=1。
又设A(x1,y1),B(x2,y2)。由圆心为(2,1),
x1+x2=4,y1+y2=2,
又![]() +
+![]() =1,
=1,![]() +
+![]() =1
=1
两式相减,得 ![]() +
+![]() = -1。
= -1。
直线AB的方程为y-1= -(x-2),即y= -x+3。
将y= -x+3代入![]() +
+![]() =1,得
=1,得
3x2-12x+18-2b2=0
直线AB与椭圆C2相交,∴Δ=24b2-72>0。
由AB=![]() x1-x2=
x1-x2=![]()
![]() =
=![]() ,
,
得![]() ·
·![]() =
=![]() 。
。
解得 b2=8,故所求椭圆方程![]() +
+![]() =1。
=1。