|
|
学科:数学 |
| 教学内容:曲线和方程 |
【基础知识精讲】
1.理解平面曲线的意义:a.曲线上的每个点都要具有某种条件
b.每个符合条件的点都要在这曲线上.
2.掌握曲线和方程的定义,理解定义中的纯粹性,完备性.
曲线的两个基本问题
本节学习要求:
求曲线的方程的步骤.
①建系设点:建立适当的坐标系,用变数对(x,y)表示曲线上任意一点M的坐标.
②立式:写出适合条件p的点M的集合p={M|p(M)}
③代换:用坐标表示条件p(M),列出方程f(x,y)=0
④化简:化方程f(x,y)=0为最简形式
⑤证明:以方程的解为坐标的点都是曲线上的点
由方程画曲线的步骤:
①讨论曲线上的对称性(关于x轴,y轴和原点)
②求截距:
方程组![]() 的解是曲线与x轴交点的坐标
的解是曲线与x轴交点的坐标
方程组![]() 的解是曲线与y轴的交点的坐标
的解是曲线与y轴的交点的坐标
③讨论曲线的范围
④列表、描点、画曲线
本节学习方法:
①循序渐近的学习方法
②具体、抽象、再具体的学习方法
③数形结合的思想
【重点难点解析】
同学们学习知识,应遵循人类认识自然,认识科学的规律,即由实践到理论,由具体到抽象的规律,因此,同学们在学习本节时,应先复习在初中学过的平面内的曲线的定义,复习数轴上的点与实数的一一对应,复习平面内的点与有序实数对的一一对应关系,从而理解掌握曲线和方程的定义.
例1 到两坐标轴距离相等的点组成的直线的方程是x-y=0吗,为什么?
分析 到两坐标轴距离相等的点组成的直线的方程不是x-y=0,因为符合题意的直线有两条,即二四象限的平分线上的点的坐标不满足方程x-y=0,即破坏了曲线和方程定义中的纯粹性.
例2 已知A(1,0),B(0,1)问线段AB的方程是不是x+y-1=0?为什么?
分析 线段AB的任一点的坐标满足x+y-1=0但是以方程x+y-1=0的解为坐标的点如(-1,2)却不在线段AB上,因此x+y-1=0不是线段AB的方程.即破坏了曲线和方程定义的完备性.
例3 已知线段AB的长为3,平面上一动点M到A的距离是到B距离的两倍,求动点的轨迹方程.
分析 先建立恰当的坐标系,注意到动点M运动到线段AB上时,有|AM|=2|MB|,点M恰为线段AB的一个三等分点,故考虑以这个三等分点为坐标原点建立直角坐标系.
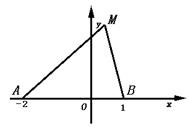
解:在线段AB上取一点O,使|AO|=2|OB|,以O为原点,AB所在直线为x轴建立如图所示的直角坐标系,则A、B两点坐标分别为(-2,0),(1,0)设动点M的坐标为(x,y),则点M属于集合p={M|MA|=2|MB|},由两点的距离公式,点M适合的条件可表示为:![]() =2
=2![]() 两边平方后化简得:x2+y2-4x=0,易验证方程x2+y2-4x=0即为所求的轨迹方程.
两边平方后化简得:x2+y2-4x=0,易验证方程x2+y2-4x=0即为所求的轨迹方程.
说明:利用直接法求轨迹方程时往往需要选择恰当的坐标系,否则,容易造成计算繁琐且方程形式复杂,本题还可以考虑以A(或B)为原点建立坐标系,或以AB的垂直平分线为y轴建立坐标系,而若延长AB至O,使|BO|=![]() |AB|,以O为坐标原点建立坐标系,以O为坐标原点建立坐标系,则有方程的最简形式x2+y2=4x.
|AB|,以O为坐标原点建立坐标系,以O为坐标原点建立坐标系,则有方程的最简形式x2+y2=4x.
【难题巧解点拨】
例1 已知直线l:![]() +
+![]() =1,M是直线l上的一个动点,过点M作x轴、y轴的垂线,垂足分别为A、B,求把有向线段
=1,M是直线l上的一个动点,过点M作x轴、y轴的垂线,垂足分别为A、B,求把有向线段![]() 分成的比λ=2的动点P的轨迹方程.
分成的比λ=2的动点P的轨迹方程.
分析 点P随已知曲线上的点M的变化而变化的动点.可分别设出P、M的坐标,并得出它们之间的关系,然后代入已知曲线即可.
解:设M(x0,y0),P(x,y),则A(x0,0),B(0,y0)
∵P分有向线段![]() 所成的比λ=2
所成的比λ=2
∴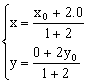
![]()
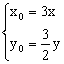
又∵M(3x, ![]() y)在直线
y)在直线![]() +
+![]() =1上,
=1上,
∴![]() x+
x+![]() =1 即 3x+2y-4=0
=1 即 3x+2y-4=0
说明:本题采用坐标代换法(或代入法)求轨迹.一般用于求“从动点”轨迹的方法:(1)分别设从动点为(x,y),主动点为(x0,y0),(2)用x,y表示x0,y0,(3)将(x0,y0)代入已知曲线方程,化简即得所求轨迹方程.
例2 已知两点P(-2,2)、Q(0,2)以及一条直线l:y=x,设长为![]() 的线段AB在直线l上移动,求直线PA和QB所在直线的交点M的轨迹方程.
的线段AB在直线l上移动,求直线PA和QB所在直线的交点M的轨迹方程.
分析 (方法一)直接法,分别设A、B坐标,写出直线方程求交点.(方法二)参数法,可设直线y=x的参数方程为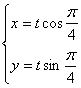 (t为参数)
(t为参数)
消参即得,![]() -
-![]() =-1
=-1
例3 如图,过定点P(3,1)有两条互相垂直的直线l1、l2,l1交x轴于M,l2交y轴于N,求线段MN中点S的轨迹方程.
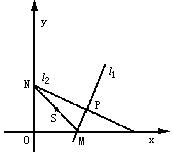
分析 显然本题的关键是要找出点S适合的条件.考虑到S是Rt△MON与Rt△MPN的斜边MN的中点,从而有|SO|=|SP|而l1与l2在运动过程中,△MON与△MPN总为直角三角形,故条件|SO|=|SP|总成立,再根据条件列出方程即可求解.
解:由题意:在Rt△MON与Rt△MPN中,S是斜边MN的中点,因此|SO|=![]() |MN|,|SP|=
|MN|,|SP|=![]() |MN|,∴|SO|=|SP|设S点的坐标为(x,y),则
|MN|,∴|SO|=|SP|设S点的坐标为(x,y),则
![]() =
=![]()
化简,整理得3x+y-5=0
即所求的点S的轨迹为3x+y-5=0
说明:曲线属于几何范畴,求曲线方程时,曲线上动点满足的几何条件是很隐蔽的,采用几何知识求曲线轨迹主要抓住图形的几何性质.
【课本难题解答】
教材第72页,习题7.6
4.答:![]() +
+![]() =1
=1
5.答:y2-8x+16=0
6.答:以两个定点所在直线为x轴,线段AB的中垂线为y轴建立直角坐标系,得点M的轨迹方程为x2+y2=4
8.答:以直线AB为x轴,线段AB的中垂线为y轴建立坐标系,得点P的轨迹方程为x2+y2=a2
9.答:7x-4y=0
【典型热点考题】
例1 如图,直线l1和l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上任意一点到l2的距离与到点N的距离相等,若△AMN为锐角三角形,|AM|=![]() ,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线段C的方程.
,|AN|=3,且|BN|=6,建立适当的坐标系,求曲线段C的方程.
分析 题中给出了相互垂直的直线l1,l2,则以l1、l2为x轴、y轴,M为坐标原点,建立坐标系的思路非常自然,设P(x,y)是曲线段C上任意一点,作PH⊥l2,H是垂足,则由题意点P满足等式|PN|=|PH|,为求得方程,只需求得N点的坐标.
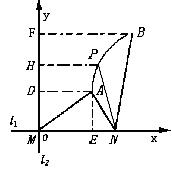
解:如上图,建立坐标系,分别以l1,l2为x轴,y轴,M为坐标原点,作AE⊥l1,AD⊥l2,BF⊥l2,垂足分别是E、D、F,设A(xa,ya),B(xb,yb),N(xn,o)
依题意有xa=|ME|=|DA|=|AN|=3,
ya=|DM|=![]() =2
=2![]()
由于△AMN是锐角三角形,故有
xn=|ME|+|EN|=|ME|+![]() =4,
=4,
xb=|BF|=|BN|=6,
设点P(x,y)中,是曲线段C上任一点,作PH⊥l2,H是垂足,则由题意知P属于集合.
{(x,y)|(x-xn)2+y2=x2,xa≤x≤xb,y>0}故曲线段C的方程为
y2=8(x-2) (3≤x≤6,y>0)
说明:本题容易忽略条件△AMN是锐角三角形这一条件,从而造成增解y2=4x.另外,求曲线方程后,要去掉不适合的点,补充上漏掉的适合条件的点,故应注意规定其范围.本题还可以直接利用抛物线的定义来解,这叫做定义法求曲线(轨迹)方程,等学了抛物线这一节后,读者便能利用新解法了.
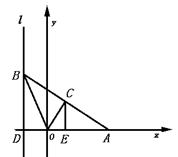
例2 如图,给出定点A(a,0)(a>0)和直线l:x=-1,B是直线l上的动点,∠BOA的角平分线交AB于C,求点C的轨迹方程.
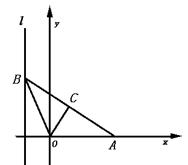
解:由题意,设B(-1,b)(b∈R)则直线OA和OB的方程分别是y=0和y=-bx,设C(x,y),则有0≤x<a,由OC平分∠AOB,点C到OA、OB的距离相等,根据点到直线的距离公式得:|y|=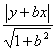 ①
①
依题意,点C在直线AB上,故有y=-![]() (x-a)
(x-a)
由x-a≠0得:b=-![]() y
②
y
②
将②代入①整理得:
y2[1+![]() ·y2]=[y-
·y2]=[y-![]() ]2
]2
即 y2[(1-a)x2-2ax+(1+a)y2]=0
若y≠0时,则
(1-a)x2-2ax+(a+1)y2=0(0≤x<a)
若y=0时,则b=0,∠AOB=π,点C的坐标为(0,0),满足上式.
综上所述,点C的轨迹方程为
(1-a)x2-2ax+(a+1)y2=(0≤x<a=
解法二:(如下图),设D是l与x轴的交点,过C作CE⊥x轴,E是垂足.
(Ⅰ)当|BD|≠0时,设C(x,y),则0<x<a,y≠0,由CE∥BD得
|BD|=![]() =
=![]() (1+a)
(1+a)
∵∠COA =∠COB=∠COD-∠BOD
=π-∠COA-∠BOD
∴2∠COA=π-∠BOD
∵tan(2∠COA)=![]()
tan(π-∠BOD)=-tan∠BOD
tan∠COA=![]()
tan∠BOD=![]() =
=![]() (1+a)
(1+a)
∴![]() =-
=-![]() (1+a)
(1+a)
整理得(1-a)x2-2ax+(1+a)y2=0(0<x<a)
(Ⅱ)当|BD|=0时,∠BOA=π,则点C的坐标为(0,0)
满足上式.综合(Ⅰ)(Ⅱ),得点C的轨迹方程为
(1-a)x2-2ax+(1+a)y2=0(0≤x<a)

【同步达纲练习】
A级
一、选择题
1.曲线f(x,y)=0关于直线x-y-2=0的对称曲线的方程为( )
A.f(y+2,x)=0 B.f(x-2,y)=0
C.f(y+2,x-2)=0 D.f(y-2,x+2)=0
2.若点M到x轴的距离和它到直线y=8的距离相等,则点M的轨迹方程是( )
A.x=-4 B.x=4 C.y=-4 D.y=4
3.动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A.y=![]() (x≠0) B.y=kx(x≠0)
(x≠0) B.y=kx(x≠0)
C.y=-![]() (x≠0) D.y=±kx(x≠0)
(x≠0) D.y=±kx(x≠0)
4.方程4x2-y2+4x+2y=0表示的曲线是( )
A.一个点 B.两条互相平行的直线
C.两条互相垂直的直线 D.两条相交但不垂直的直线
5.已知点A(0,-1),点B是抛物线y=2x2+1上的一个动点,则线段AB的中点的轨迹是( )
A.抛物线y=2x2 B.抛物线y=4x2
C.抛物线y=6x2 D.抛物线y=8x2
二、填空题
6.已知A(-1,0),B(2,4),且△ABC的面积是10,则点C的轨迹方程是 .
7.Rt△ABC的斜边AB的长度等于定值C,顶点A、B在x轴,y轴上滑动,则斜边AB的中点M的轨迹方程为
8.到两平行线3x+2y-1=0和6x+4y-3=0的距离相等的点的轨迹方程为 .
三、解答题
9.已知直线l:![]() +
+ ![]() =1,M是直线l上的一个动点,过点M作x轴,y轴的垂线,垂足分别为A、B求把有向线段
=1,M是直线l上的一个动点,过点M作x轴,y轴的垂线,垂足分别为A、B求把有向线段![]() 分成的比λ=2的动点P的轨迹方程.
分成的比λ=2的动点P的轨迹方程.
10.经过点P(3,2)的一条动直线分别交x轴、y轴于点A、B,M是线段AB的中点,连结OM并延长至点N,使|ON|=2|OM|,求点N的轨迹方程.
AA级
一、选择题
1.下列各点中,在曲线x2-xy+2y+1=0上的点是( )
A.(2,-2) B.(4,-3) C.(3,10) D.(-2,5)
2.已知坐标满足方程f(x,y)=0的点都在曲线C上,则( )
A.曲线C上的点的坐标都适合方程f(x,y)=0
B.坐标不适合方程f(x,y)=0的点都不在曲线C上
C.不在曲线C上的点的坐标都不适合方程f(x,y)=0
D.不在曲线C上的点的坐标一定有些适合,也有一些不适合方程f(x,y)=0
3.到两条坐标轴的距离之和等于2的点的轨迹方程是( )
A.x+y=2 B.x+y=±2
C.|x|+|y|=2 D.|x+y|=2
4.到直线l:3x+4y-5=0的距离等于1的点的轨迹方程是( )
A.3x+4y-4=0 B.3x+4y=0或3x+4y-10=0
C.3x+4y+10=0 D.3x+4y-30=0或3x+4y+20=0
5.与A(-1,0)和B(1,0)两点连线的斜率的乘积等于-1的动点P的轨迹方程是( )
A.x2+y2=1 B.x2+y2=1(x≠±1)
C.x2+y2=1(x≠0) D.y=![]()
二、填空题
6.若点P在曲线y=x2+1上,且点P到原点的距离为![]() ,则点P的坐标为 .
,则点P的坐标为 .
7.若两直线x+y=3a,x-y=a的交点在方程x2+y2=1所表示的曲线上,则a= .
8.点P到定点F(4,0)的距离比它到定直线x+5=0的距离小1,则动点P的轨迹方程是 .
三、解答题
9.已知曲线C上的每一点到点A(0,-2)的距离与它到x轴的距离的差等于2,求这条曲线的方程,并画出这条曲线.
10.在△ABC中,AB边的长为2a,若BC边上的中线AD的长为m,试求顶点C的轨迹方程.
【素质优化训练】
一、选择题
1.方程(2x+y)(x+y-3)=0与(4x+2y+1)(2x-y+1)=0所表示的两曲线的公共点个数是( )
A.1个 B.2个 C.3个 D.多于3个
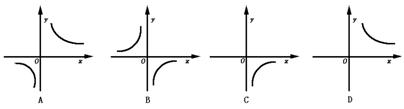
2.方程arccotx+arccoty=π所表示的示意曲线是( )
3.已知△ABC的两个顶点坐标为A(-2,0),B(2,0)第三个顶点C在直线2x-3y+5=0上,则△ABC的重心G的轨迹方程为( )
A.2x-3y+5=0(y≠0) B.6x-9y+5=0(y≠0)
C.6x-3y+5=0(x≠0) D.6x-9y+5=0(x≠0)
4.方程|x|+|y|=1的曲线的周长及其所围成的区域的面积分别为( )
A.2![]() ,1 B.4
,1 B.4![]() ,2 C.6
,2 C.6![]() ,4 D.8,4
,4 D.8,4
5.方程x+y-4![]() +2m=0表示一条直线,则实数m满足( )
+2m=0表示一条直线,则实数m满足( )
A.m=0 B.m=2
C.m=2或m<0 D.m≥2
二、填空题
6.线段AB和CD互相垂直平分于点O,|AB|=2,|CD|=4,动点P满足|PA|·|PB|=|PC|·|PD|,则动点P的轨迹方程为 .
7.点P(x,y)在直线x+2y+1=0上移动,并在函数u=2x+4y取得最小值,则P点坐标为 .
8.已知关于x,y的方程x2-4xy+my2-x+(3m-10)y-2=0表示两条直线,则m= .
三、解答题
9.求两直线l1:x-3my+3=0,l2,3mx+y+9m=0的交点的轨迹,并画出轨迹的图形.
10.设等腰三角形OAB的顶角为2θ,高为h
(1)△OAB内有一动点P到三边OA、OB,AB的距离分别为|PD|、|PF|、|PE|,且满足关系:
|PD|·|PF|=|PE|2,求P点的轨迹.
(2)在上述轨迹中定出P点的坐标,使得|PD|+|PE|=|PF|
【知识探究学习】
如图所示是某防空部队进行射击训练时在平面直角坐标系中的示意图,在地面O、A两个观点测得空中固定目标C的仰角分别为α和β,OA=1千米,tanα=![]() ,tanβ=
,tanβ=![]() ,位于O点正上方
,位于O点正上方![]() 千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
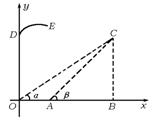
解:能否击中C点,关键是看一下C点是否在导弹飞行的轨迹上,因此应选求C点坐标,然后求轨迹的方程,再验证该点是否满足轨迹方程.
设抛物线为y=a(x-4)2+3,由抛物线过点(0, ![]() ),求得a=-
),求得a=-![]() .
.
所以 y=-![]() (x-4)2+3
(x-4)2+3
=-![]() x2+
x2+![]() x+
x+![]() .
.
设C点坐标为(x0,y0),过C作CB⊥Ox于B,
tanα=![]() =
=![]() ,tanβ=
,tanβ=![]() =
=![]() .
.
则![]() x0=
x0=![]() (x0-1).
(x0-1).
解得x0=7,求出y0=![]() .
.
即C点坐标为(7,![]() ),经计算
),经计算
-![]() x02+
x02+![]() x0+
x0+![]() =-
=-![]() ×72+
×72+![]() ×7+
×7+![]() =
=![]() .
.
所以C点在抛物线上.
故依轨道运行的导弹可以击中目标C.

参考答案:
【同步达纲练习】
A级
1.C 2.D
3.D 4.D 5.B
6.4x-3y+24=0或4x-3y-16=0 7.x2+y2=![]() 8.12x+8y-5=0 9.3x+2y-4=0 10.
8.12x+8y-5=0 9.3x+2y-4=0 10.![]() +
+![]() =1
=1
AA级
1.C 2.C 3.C 4.B 5.B
6.(±1,2)
7.±![]() 8.y2=16x 9.x=0(y>0)或x2=-8y(y≤0) 10.(x+3a)2+y2=4m2
8.y2=16x 9.x=0(y>0)或x2=-8y(y≤0) 10.(x+3a)2+y2=4m2
【素质优化训练】
1.C 2.C 3.B 4.B 5.C
6.2x2-2y2+3=0 7.(- ![]() ,-
,-![]() ) 8.3或4 9.x2+y2=9(x≠0)
) 8.3或4 9.x2+y2=9(x≠0)
10.(1)(x-hsec2θ)2+y2=h2tan2θsec2θ (2)P(![]() ,
,![]() )
)
