|
|
学科:数学 |
| 教学内容:双曲线的简单几何性质 |
【基础知识精讲】
1.双曲线![]() -
-![]() =1的简单几何性质
=1的简单几何性质
(1)范围:|x|≥a,y∈R.
(2)对称性:双曲线的对称性与椭圆完全相同,关于x轴、y轴及原点中心对称.
(3)顶点:两个顶点A1(-a,0),A2(a,0),两顶点间的线段为实轴,长为
(4)渐近线:双曲线特有的性质,方程y=±![]() x,或令双曲线标准方程
x,或令双曲线标准方程![]() -
-![]() =1中的1为零即得渐近线方程.
=1中的1为零即得渐近线方程.
(5)离心率e=![]() >1,随着e的增大,双曲线张口逐渐变得开阔.
>1,随着e的增大,双曲线张口逐渐变得开阔.
(6)等轴双曲线(等边双曲线):x2-y2=a2(a≠0),它的渐近线方程为y=±x,离心率e=![]() .
.
(7)共轭双曲线:方程![]() -
-![]() =1与
=1与![]() -
-![]() =-1表示的双曲线共轭,有共同的渐近线和相等的焦距,但需注意方程的表达形式.
=-1表示的双曲线共轭,有共同的渐近线和相等的焦距,但需注意方程的表达形式.
注意:
1.与双曲线![]() -
-![]() =1共渐近线的双曲线系方程可表示为
=1共渐近线的双曲线系方程可表示为![]() -
-![]() =λ(λ≠0且λ为待定常数)
=λ(λ≠0且λ为待定常数)
2.与椭圆![]() +
+![]() =1(a>b>0)共焦点的曲线系方程可表示为
=1(a>b>0)共焦点的曲线系方程可表示为![]() -
-![]() =1(λ<a2,其中b2-λ>0时为椭圆, b2<λ<a2时为双曲线)
=1(λ<a2,其中b2-λ>0时为椭圆, b2<λ<a2时为双曲线)
2.双曲线的第二定义
平面内到定点F(c,0)的距离和到定直线l:x=![]() 的距离之比等于常数e=
的距离之比等于常数e=![]() (c>a>0)的点的轨迹是双曲线,定点是双曲线的焦点,定直线是双曲线的准线,焦准距(焦参数)p=
(c>a>0)的点的轨迹是双曲线,定点是双曲线的焦点,定直线是双曲线的准线,焦准距(焦参数)p=![]() ,与椭圆相同.
,与椭圆相同.
3.焦半径(![]() -
-![]() =1,F1(-c,0)、F2(c,0)),点p(x0,y0)在双曲线
=1,F1(-c,0)、F2(c,0)),点p(x0,y0)在双曲线![]() -
-![]() =1的右支上时,|pF1|=ex0+a,|pF2|=ex0-a;
=1的右支上时,|pF1|=ex0+a,|pF2|=ex0-a;
P在左支上时,则 |PF1|-(ex1+a),
|PF2|=-(ex1-a).
本节学习要求:
学习双曲线的几何性质,可以用类比思想,即象讨论椭圆的几何性质一样去研究双曲线的标准方程,从而得出双曲线的几何性质,将双曲线的两种标准方程、图形、几何性质列表对比,便于掌握.
双曲线的几何性质与代数中的方程、平面几何的知识联系密切;直线与双曲线的交点问题、弦长间问题都离不开一元二次方程的判别式,韦达定理等;渐近线的夹角问题与直线的夹角公式.三角函数中的相关知识,是高考的主要内容.
通过本节内容的学习,培养同学们良好的个性品质和科学态度,培养同学们的良好的学习习惯和创新精神,进行辩证唯物主义世界观教育.
【重点难点解析】
1.学习双曲线的几何性质,也可以与椭圆的几何性质对比进行,着重指出它们的联系和区别.
2.本节重点是双曲线的几何性质,双曲线的第二定义及其应用,难点是双曲线的渐近线方程,第二定义,几何性质的应用.
例1 (1)求中心在原点,对称轴是坐标轴,一条渐近线方程是y=-![]() x,且经过点Q(8,6
x,且经过点Q(8,6![]() )的双曲线方程.
)的双曲线方程.
(2)已知双曲线满足:两准线间的距离为![]() ,渐近线方程为y=±
,渐近线方程为y=±![]() x,求双曲线方程.
x,求双曲线方程.
分析 (1)据双曲线的渐近线方程,可求出a,b之间的关系,以Q点的坐标代入双曲线方程,即可求a,b的值,亦可据共渐近线的双曲线系方程求出,这样可据焦点所在坐标轴的讨论.即设双曲线方程为![]() -
-![]() =λ(λ≠0),将Q点坐标代入求得 λ=4
=λ(λ≠0),将Q点坐标代入求得 λ=4
故所求双曲线方程为 ![]() -
-![]() =1.
=1.
(2)当双曲线的焦点在x轴上时,设其方程为
![]() -
-![]() =1,依题意有
=1,依题意有
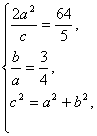 解得
解得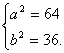
故所求双曲线方程为 ![]() -
-![]() =1
=1
当双曲线焦点在y轴上时,同理求得其方程为:![]() -
-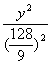 =1
=1
综上所述,所求双曲线的方程为
![]() -
-![]() =1或
=1或![]() -
-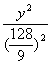 =1.
=1.
例2 过双曲线![]() -
-![]() =1的右焦点F2,作斜率为2的弦AB,求|AB|的长.
=1的右焦点F2,作斜率为2的弦AB,求|AB|的长.
分析 运用焦半径知识较为简便.
依题意有a=3,c=5,e=![]() ,F2(5,0)
,F2(5,0)
联立方程组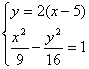
消去y得 5x2-90x+261=0.
设方程的两根为x1,x2.
于是|AB|=e(x1+x2)-2a=![]() ×
×![]() -6=24.
-6=24.
注:若用弦长|AB|=![]() ·
·![]() 解计算量显然大一些,本例中AB为过焦点弦,所以运用焦半径解题就较自然了.
解计算量显然大一些,本例中AB为过焦点弦,所以运用焦半径解题就较自然了.
例3 已知直线l和双曲线![]() -
-![]() =1(a>0,b>0)及其渐近线依次交于A、B、C、D四点,求证:|AB|=|CD|.
=1(a>0,b>0)及其渐近线依次交于A、B、C、D四点,求证:|AB|=|CD|.
分析 若直线l和x轴垂直,结论显然成立;若直线l不与x轴垂直,则可设l的方程为y=kx+m,代入双曲线方程并整理得:
(b2-a2k2)x2-2a2kmx-a2(m2+b2)=0,
设A(x1,y1),D(x2,y2),则x1+x2=![]() 再将y=kx+m代入双曲线渐近线方程
再将y=kx+m代入双曲线渐近线方程
b2x2-a2y2=0 并整理得
(b2-a2k2)x2-2a2kmx-a2m2=0.
设B(x3,y3),C(x4,y4),则x3+x4=![]()
∴x1+x2=x3+x4
表明线段AD的中点和线段BC的中点重合,故问题得到证明.
【难题巧解点拨】
例1 求与双曲线![]() -
-![]() =1有共同渐近线且过点(2,3)的双曲线方程.
=1有共同渐近线且过点(2,3)的双曲线方程.
分析一 只要判断清楚已知点(2,3)与渐近线的位置关系,便可知双曲线方程的表达式,进而可求出方程.
解法一:双曲线![]() -
-![]() =1的渐近线方程为:y=±
=1的渐近线方程为:y=±![]() x
x
将x=2代入方程y=![]() x得y=
x得y=![]() ·2=
·2=![]() <3
<3
∴点(2,3)在直线y=![]() x的上方,于是设所求的双曲线方程为:
x的上方,于是设所求的双曲线方程为:
![]() -
-![]() =1
=1
∴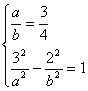
![]()
由(1)设a=3k,b=4k,代入(2)得:![]() -
-![]() =1
=1
∴k=±![]() (舍负)
(舍负)
∴a=3![]() b=2
b=2![]()
∴所求方程为:![]() -
-![]() =1即
=1即![]() -
-![]() =1
=1
分析二 与双曲线![]() -
-![]() =1有共同渐近线的双曲线方程表示为
=1有共同渐近线的双曲线方程表示为![]() -
-![]() =λ,待定系数λ便可求出双曲线方程.
=λ,待定系数λ便可求出双曲线方程.
解法二:设所求双曲线方程为
![]() -
-![]() =λ,(1)
=λ,(1)
将点(2,3)代入(1)得:
![]() -
-![]() =λ ∴λ=-
=λ ∴λ=-![]() 所求方程为:
所求方程为:![]() -
-![]() =-
=-![]()
即:![]() -
-![]() =1为所求
=1为所求
说明:(1)由渐近线及一点可以确定双曲线的位置,解法一正是利用此性质先定位再求出a、b,进而求出双曲线方程.
(2)方程![]() -
-![]() =λ 当λ=0时,表示两条直线:
=λ 当λ=0时,表示两条直线:![]() +
+![]() =0和
=0和![]() -
-![]() =0,正是双曲线的渐近线方程.因此当λ≠0时,方程表示以直线
=0,正是双曲线的渐近线方程.因此当λ≠0时,方程表示以直线![]() -
-![]() =0为渐近线的双曲线系.解法二正是利用了此原理,设方程再代入点坐标便可求出双曲线方程比较简捷.
=0为渐近线的双曲线系.解法二正是利用了此原理,设方程再代入点坐标便可求出双曲线方程比较简捷.
例2 在双曲线![]() -
-![]() =1的一支上不同的三点A(x1,y1)、B(
=1的一支上不同的三点A(x1,y1)、B(![]() ,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
,6)、C(x2,y2)与焦点F(0,5)的距离成等差数列.
(1)求y1+y2;
(2)证明线段AC的垂直平分线经过某一定点,并求该定点的坐标.
分析 (1)从双曲线的焦半径分析往往用第二定义.
(2)证明过定点可采取求点坐标的方法.
解:(1)∵a=2![]() ,b=
,b=![]() ,c=5,
,c=5,
∴e=![]() =
=![]() =
=![]() .
.
根据双曲线的第二定义,可得:
|AF|=e(y1-![]() )=ey1-a=
)=ey1-a=![]() y1-2
y1-2![]() ,
,
|CF|=e(y2-![]() )=ey2-a=
)=ey2-a=![]() y2-2
y2-2![]() ,
,
|BF|=e(6-![]() )=6e-a=6×
)=6e-a=6×![]() -2
-2![]() =3
=3![]() .
.
又|AF|、|BF|、|CF|成等差数列,∴|AF|+|CF|=2|BF|,即(![]() y1-2
y1-2![]() )+(
)+( ![]() y2-2
y2-2![]() )=2×3
)=2×3![]() ,∴y1+y2=12.
,∴y1+y2=12.
(2)证明:设x1+x2=t,则线段AC的中点为(![]() ,6).∵
,6).∵![]() -
-![]() =1,
=1, ![]() -
-![]() =1.
=1.
∴![]() -
-![]() =0,
=0,
∴![]() =
=![]() (x1+x2)=
(x1+x2)=![]() .
.
∴线段AC的垂直平分线的斜率k=-![]() ,从而其方程为y-6=-
,从而其方程为y-6=-![]() (x-
(x-![]() ),即(y-
),即(y-![]() )t+3x=0,显然它过定点(0,
)t+3x=0,显然它过定点(0,![]() ).
).
点评:涉及焦半径问题往往考虑第二定义,一般来讲,双曲线![]() -
-![]() =1上一点P(x1,y1)的左、右焦半径长为|PF1|=±(ex1+a),|PF2|=±(ex1-a)(其中P在右支上取正号,在左支上取负号).
=1上一点P(x1,y1)的左、右焦半径长为|PF1|=±(ex1+a),|PF2|=±(ex1-a)(其中P在右支上取正号,在左支上取负号).
【典型热点考题】
例1 已知双曲线![]() -
-![]() =1(a>0,b>0)左、右焦点分别为F1和F2,P是它左支上点,P到左准线距离为d.
=1(a>0,b>0)左、右焦点分别为F1和F2,P是它左支上点,P到左准线距离为d.
问:是否存在这样的点P,使d,|PF1|,|PF2|成等比数列,说明理由.
分析 对于存在性问题,先假设存在满足题意的对象,然后结合题设条件进行判断.
设存在P(x0,y0)且x0≤-a,使d,|PF1|,|PF2|成等比数列,则|PF1|2=d|PF2|,
设d′为P点到右准线的距离,由双曲线第二定义得:
![]() =
=![]() =e ∴|PF1|=ed,
=e ∴|PF1|=ed,
∴(ed)2=d·ed′,∴ed=d′,
∴e(-![]() -x0)=-x0+
-x0)=-x0+![]() ,
,
∴x0=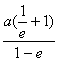 ∵x0≤-a,
∵x0≤-a,
∴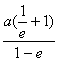 ≤-a,∴e2-2e-1≤0,
≤-a,∴e2-2e-1≤0,
∴1-![]() ≤e≤
≤e≤![]() +1,又e>1,
+1,又e>1,
∴1<e≤![]() +1.
+1.
故当双曲线的离心率e∈(1, ![]() +1)时,存在满足条件的P,而当e∈(
+1)时,存在满足条件的P,而当e∈(![]() +1,+∞)时,不存在满足条件的点P.
+1,+∞)时,不存在满足条件的点P.
注:利用双曲线的第二定义解题是非常有效的方法.本例还可以利用双曲线的两种定义再结合不等式|PF1|+|PF2|≥|F1F2|求解,请同学们自己完成.
例2 如图,已知梯形ABCD中,|AB|=2|CD|,点E分有向线段![]() 所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当(
所成的比为λ,双曲线过C、D、E三点,且以A、B为焦点.当(![]() ≤λ≤
≤λ≤![]() )时,求双曲线离心率e的取值范围.
)时,求双曲线离心率e的取值范围.
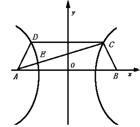
分析 如图,以AB的垂直平分线为y轴,直线AB为x轴,建立直角坐标系,则CD⊥y轴.
因为双曲线经过点C、D,且以A、B为焦点,由双曲线的对称性知C、D关于y轴对称.依题意,记A(-C,0),C(![]() ,h),E(x0,y0,)其中c=
,h),E(x0,y0,)其中c=![]() |AB|为双曲线的半焦距,h是梯形的高.
|AB|为双曲线的半焦距,h是梯形的高.
由定比分点坐标公式得
x0=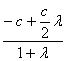 =
=![]() ,y0=
,y0=![]()
![]() -
-![]() =1, ①
=1, ①
![]() (
(![]() )2-(
)2-(![]() )2
)2![]() =1 ②
=1 ②
由①式得![]() =
=![]() -1 ③
-1 ③
把③式代入②式,整理得
![]() (4-4λ)=1+2λ
(4-4λ)=1+2λ
故λ=1-![]()
由题设 ![]() ≤λ≤
≤λ≤![]() 得
得![]() ≤1-
≤1-![]() ≤
≤![]() .
.
解得 ![]() ≤e≤
≤e≤![]() .
.
所以双曲线的离心率的取值范围为[![]() ,
,![]() ].
].
注:本例先求出C点纵坐标,用a、b、c表示,然后将E点坐标用λ表示,并代入双曲线方程,而得到含有e与λ的等式,由λ范围求出e的范围.
例3 已知双曲线的两个焦点分别为M、N,点M的坐标为(-2,-12),点S(-7,0)、T(7,0)在双曲线.
(1)利用双曲线定义,求点N的轨迹方程;
(2)是否存在过P(1,m)的直线与点N的轨迹有且只有两个公共点A、B,且点P(1,m)恰是线段AB的中点?若存在,求出实数m的取值范围;若不存在,说明理由.
分析 (1)设点N的坐标为(x,y),它不同于点M(-2,-12).由双曲线定义知
||SM|-|SN||=||TM|-|TN||≠0
∵S(-7,0),T(7,0),∴|SM|=13,|TM|=15.
1°当|SM|-|SN|=|TM|-|TN|时,有|TN|-|SN|=2<14=|ST|,
∴点N的轨迹是中心在ST的中点(0,0),焦点为S、T的双曲线C的左支,除去M(-2,-12)和D(-2,12)两点.
双曲线C的方程:x2-![]() =1(x<0).
=1(x<0).
∴点N的轨迹方程为
x2-![]() =1(x<0,y≠±12).
=1(x<0,y≠±12).
2°当|SM|-|SN|=-(|TM|-|TN|)时,有|TN|+|SN|=28>14=|ST|,
∴点N的轨迹是中心在ST的中点(0,0),焦点为S、T的椭圆Q,除去M(-2,-12)和D(-2,12)两点.
椭圆Q方程:![]() +
+![]() =1.
=1.
∴点N的轨迹方程为![]() +
+![]() =1(y≠±12).
=1(y≠±12).
综合1°、2°,点N的轨迹方程为
x2-![]() =1(x<0=和
=1(x<0=和![]() +
+![]() =1,其中y≠±12.
=1,其中y≠±12.
(2)1°当过点P(1,m)的直线的斜率k不存在时,直线l的方程为x=1,可得m=1.
2°当k存在时,设直线l:y=kx+m-k.若l过点M或点D.
∵两点M、D既在双曲线C上,又在椭圆Q上,但不在点N的轨迹上
∴l与点N的轨迹只有一个公共点,不合题意;若l不过M、D两点.
当-4![]() <k2<4
<k2<4![]() 时(双曲线C的渐近线方程为y±4
时(双曲线C的渐近线方程为y±4![]() =0),利用图像知,直线l与点N的轨迹有三个公共点,不合题意.
=0),利用图像知,直线l与点N的轨迹有三个公共点,不合题意.
当-∞<k≤-4![]() 或4
或4![]() <k≤+∞时,
<k≤+∞时,
直线l与点N的轨迹有两个公共点A、B,且点P(1,m)是AB的中点.
设A(x1,y1),B(x2,y2),则在
3x21+4y21=12×49, ①
3x22+4y22=12×49, ②
①-②,得3(x1+x2)(x1-x2)=-4(y1+y2)(y1-y2) ③
将x1+x2=2,y1+y2=2m,![]() =k代入③,得k=-
=k代入③,得k=-![]() .
.
当4![]() ≤k<+∞,即4
≤k<+∞,即4![]() ≤-
≤-![]() <+∞时,有-
<+∞时,有-![]() ≤m<0.
≤m<0.

【同步达纲练习】
A级
一、选择题
1.已知双曲线kx2-2ky2=4的一条准线是y=1,则实数k的值等于( )
A.![]() B.-
B.-![]() C.-
C.-![]() D.
D.![]()
2.双曲线与其共轭双曲线有相同的( )
A.顶点 B.焦点 C.准线 D.渐近线
3.过点(2,-2)且与双曲线x2-2y2=2有公共渐近线的双曲线方程是( )
A.-![]() +
+![]() =1 B.
=1 B.
![]() -
-![]() =1
=1
C.- ![]() +
+![]() =1 D.
=1 D.
![]() +
+![]() =1
=1
4.已知双曲线的半焦距为C,两准线间的距离为d,且c=d,则双曲线的离心率等于( )
A. ![]() B.
B.![]() C.3 D.2
C.3 D.2
5.当8<k<17时,曲线![]() +
+![]() =1与
=1与![]() +
+![]() =1有相同的( )
=1有相同的( )
A.焦距 B.准线 C.焦点 D.离心率
二、填空题
6.以y=±![]() x为渐近线,且焦点在坐标轴上,焦距为10的双曲线
.
x为渐近线,且焦点在坐标轴上,焦距为10的双曲线
.
7.双曲线![]() -
-![]() =1的两准线相距 ,两渐近线所夹的锐角等于
;
=1的两准线相距 ,两渐近线所夹的锐角等于
;
8.若双曲线的离心率为2,则其共轭双曲线的离心率为 .
三、解答题
9.试求以椭圆![]() +
+![]() =1的右焦点为圆心,且与双曲线
=1的右焦点为圆心,且与双曲线![]() -
-![]() =1的渐近线相切的圆方程.
=1的渐近线相切的圆方程.
10.过双曲线![]() -
-![]() =1的右焦点F作倾斜角为
=1的右焦点F作倾斜角为![]() 的弦AB,求弦AB的长及AB的中点M到右焦点F的距离.
的弦AB,求弦AB的长及AB的中点M到右焦点F的距离.
AA级
一、选择题
1.在下列双曲线中,与双曲线![]() -y2=1的离心率和渐近线都相同的是( )
-y2=1的离心率和渐近线都相同的是( )
A.3y2-x2=9 B.x2-3y2=9
C.3y2-9x2=1 D.3x2-y2=3
2.双曲线的两条渐近线方程为y=±![]() x,则双曲线的离心率为( )
x,则双曲线的离心率为( )
A.![]() B.2 C.
B.2 C.![]() 或
或![]() D.
D.
![]() 或
或![]()
3.过双曲线的一个焦点且与双曲线的实轴垂直的弦叫做双曲线的通径,则双曲线![]() -
-![]() =1的通径的长是( )
=1的通径的长是( )
A. ![]() B.
B.
![]() C.9 D.10
C.9 D.10
4.已知双曲线![]() -
-![]() =1上的一点P到右焦点的距离为14,则P点到左准线的距离为( )
=1上的一点P到右焦点的距离为14,则P点到左准线的距离为( )
A.22 B.24 C.26 D.28
5.已知双曲线x2-y2=1的左焦点为F,点P为双曲线在第三象限内的任意一点,则斜率kPF的取值范围是( )
A.k≤0或k≥1 B.k<0或k>1
C.k≤-1或k≥1 D.k<-1或k>1
二、填空题
6.双曲线16x2-9y2=144上一点P(x0,y0)(x0<0)到左焦点距离为4,则x0= .
7.双曲线![]() -y2=1的共轭双曲线的准线方程是
.
-y2=1的共轭双曲线的准线方程是
.
8.双曲线![]() -
-![]() =1的准线和渐近线的交点到双曲线的中心的距离等于
.
=1的准线和渐近线的交点到双曲线的中心的距离等于
.
三、解答题
9.直线y=kx+1与双曲线x2-y2=1的左支交于A、B两点,直线l过点(-2,0)和AB中点,求直线l在y轴上截距b的取值范围.
10.求证:以过双曲线的一个焦点的弦为直径的圆,必与对应的准线相交,且这条准线截得的劣弧的弧度数为定值.
【素质优化训练】
1.过点A(1,1)且与双曲线x2-y2=2有且只有一个公共点的直线的条数是( )
A.1 B.2 C.3 D.4
2.双曲线的两条准线分焦点间的距离成三等分,则双曲线的离心率为( )
A.![]() B.
B.
![]() C.
C.![]() D.2
D.2
3.若双曲线的两条渐近线是y=±![]() x,焦点F1(-
x,焦点F1(-![]() ,0),F2(
,0),F2(![]() ,0),那么它的两条准线间的距离是( )
,0),那么它的两条准线间的距离是( )
A. ![]() B.
B.![]() C.
C.
![]() D.
D.
![]()
4.已知双曲线的两个焦点是椭圆16x2+25y2=160的两个顶点,双曲线的两准线分别过椭圆的两个焦点,则此双曲线的方程是( )
A. ![]() -
-![]() =1 B.
=1 B.
![]() -
-![]() =1
=1
C.![]() -
-![]() =1 D.
=1 D.![]() -
-![]() =1
=1
5.已知E、F分别是离心率为![]() 的双曲线
的双曲线![]() -
-![]() =1(a>0,b>0)的左顶点与右焦点,记M(0,b),则∠EMF等于( )
=1(a>0,b>0)的左顶点与右焦点,记M(0,b),则∠EMF等于( )
A.45° B.60° C.90° D.120°
二、填空题
6.已知双曲线![]() -
-![]() =1和点A(6,2)、B(5,0),M是双曲线上的一个动点,则
=1和点A(6,2)、B(5,0),M是双曲线上的一个动点,则![]() |MA|+|MB|的最小值为
.
|MA|+|MB|的最小值为
.
7.双曲线的离心率是e=3,则两渐近线的夹角是 .
8.渐近线为y=±![]() x,且和直线5x-6y-8=0有且仅有一个公共点的双曲线方程为 .
x,且和直线5x-6y-8=0有且仅有一个公共点的双曲线方程为 .
三、解答题
9.已知点A(![]() ,0)和曲线y=
,0)和曲线y=![]() (2≤x≤2
(2≤x≤2![]() )上的点P1,P2,…,Pn,若|P1A|,|P2A|,…,|PnA|成等差数列并且公差d∈(
)上的点P1,P2,…,Pn,若|P1A|,|P2A|,…,|PnA|成等差数列并且公差d∈(![]() ,
,![]() ),求n的最大值.
),求n的最大值.
10.已知双曲线![]() -
-![]() =1(a>0,b>0)离心率e=
=1(a>0,b>0)离心率e=![]()
![]() ,过点A(0,-b)和B(a,0)的直线与原点间距离
,过点A(0,-b)和B(a,0)的直线与原点间距离![]() .
.
(1)求双曲线方程;
(2)直线y=kx+m(k≠0,m≠0)与双曲线交于不同的两点C、D,且C、D两点都在以A为圆心的同一圆上,求m的取值范围.
【生活实际运用】
1.运用双曲线的光学性质,设计并制作一台灯或吊灯.
2.双曲线型自然通风塔的外形,是双曲线的一部分绕其虚构旋转所成的曲面,它的最小半径是6米,最小半径处的截口平面到地面距离是5米,底面截口半径是10米,求此双曲线的标准方程.
注:这是一个有实际意义的题目.解这类题目时,首先要确认以下两个问题:(1)选择适当的坐标系;(2)将实际问题中的条件借助坐标系用数学语言表达出来.双曲线的标准方程为![]() -
-![]() =1.
=1.
【知识验证实验】
1.已知双曲线2x2-y2=2,试问过点N(1,1)能否作一直线与双曲线交于C、D两点,且使N为CD的中点?这样的直线如果存在,求出它的方程,如果不存在,则说明理由.
将问题一般化:N(x0,y0),双曲线方程为![]() -
-![]() =1,若过点N的双曲线的中点弦存在,则N点应在什么位置?其方程又为何?
=1,若过点N的双曲线的中点弦存在,则N点应在什么位置?其方程又为何?
2.点P是双曲线![]() -
-![]() =1右分支上任意一点,F1,F2分别为左、右焦点,设∠PF1F2=α,∠PF2F1=β,求证:3tan
=1右分支上任意一点,F1,F2分别为左、右焦点,设∠PF1F2=α,∠PF2F1=β,求证:3tan![]() =tan
=tan![]() .
.
解:在△PF1F2中,利用正弦定理及分比定理得![]() =
=![]() =
=![]() =
=![]() ,
,
∴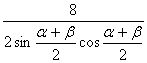 =
=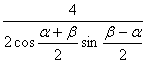 ,即2sin
,即2sin![]() =sin
=sin![]() ,展开并简化,得3sin
,展开并简化,得3sin![]() cos
cos![]() =sin
=sin![]() cos
cos![]() ,
,
∴3tan![]() =tan
=tan![]() .
.
【知识探究学习】
舰A在舰B的正东6km处,舰C在舰B的北偏西30°且与B相距4千米处,它们准备围捕海洋动物.某时刻A发现动物信号,4s后B、C同时发现这种信号,A发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度是1km/s,炮弹的速度是![]() km/s,其中g为重力加速度.若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
km/s,其中g为重力加速度.若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
解:取AB所在直线为x轴,AB中点为原点建立直角坐标系,则A、B、C舰的坐标分别为(3,0)、(-3,0)、(-5,2![]() ).
).
记动物所在位置为P,则|PB|=|PC|,于是P在BC中垂线上,其方程为![]() x-3y+7
x-3y+7![]() =0.
=0.
又A、C两舰发现信号的时间差为4秒,有|PB|-|PA|=4,于是P在双曲线![]() -
-![]() =1的右支上,求得P点坐标是(8,5
=1的右支上,求得P点坐标是(8,5![]() )且|PA|=10.
)且|PA|=10.
又kPA=![]() ,∴直线PA的倾斜角为60°,于是舰A发射炮弹的方位角是北偏东30°,
,∴直线PA的倾斜角为60°,于是舰A发射炮弹的方位角是北偏东30°,
设发射的仰角是θ,初速度为v0=![]() ,则
,则![]() =
=![]() ,
,
∴sin2θ=![]() =
=![]() ,
,
∴仰角θ=30°

参考答案:
【同步达纲练习】
A级
1.B 2.D
3.A 4.B 5.A
6. ![]() -
-![]() =1或
=1或![]() -
-![]() =-1 7.
=-1 7. ![]() ,arctan2
,arctan2![]() 8.
8. ![]()
9.解:由椭圆![]() +
+![]() =1的右焦点为(5,0),∴圆心为(5,0),又圆与双曲线
=1的右焦点为(5,0),∴圆心为(5,0),又圆与双曲线![]() -
-![]() =1的渐近线相切,即圆心到直线y=±
=1的渐近线相切,即圆心到直线y=±![]() x的距离为圆的半径.∴r=
x的距离为圆的半径.∴r=![]() =4 于是圆的方程为(x-5)2+y2=16.
=4 于是圆的方程为(x-5)2+y2=16.
10.解:∵F(5,0),∴AB:y=x-5,将AB的方程代入双曲方程,得7x2+90x-369=0,设A(x1,y1),B(x2,y2),则x1+x2=-![]() ,x1x2=-
,x1x2=-![]() ,∴|AB|=
,∴|AB|=![]() =
=![]() =
=![]() ,又xm=
,又xm=![]() =-
=-![]() ,∴|MF|=
,∴|MF|=![]() |xM-5|=
|xM-5|=![]()
AA级
1.B 2.C
3.B 4.B 5.B
6.-![]() 7.y=±
7.y=±![]() 8.a
8.a
9.解:由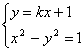 消去y得,(1-k2)x2-2kx-2=0,若令f(x)=(1-k2)x2-2kx-2,则直线与双曲线左支相交于A、B两点,等价于方程f(x)=0有两个不大于-1的不等实根,即:
消去y得,(1-k2)x2-2kx-2=0,若令f(x)=(1-k2)x2-2kx-2,则直线与双曲线左支相交于A、B两点,等价于方程f(x)=0有两个不大于-1的不等实根,即: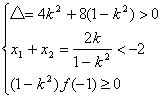 解得1<k<
解得1<k<![]() ,又AB中点为(
,又AB中点为(![]() ,
,![]() ),∴直线l的方程为
),∴直线l的方程为![]() =
=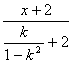
![]() y=
y=![]() ,令x=0,b=
,令x=0,b=![]() =
=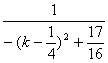 ,由k∈(1,
,由k∈(1, ![]() )知b<-2-
)知b<-2-![]() 或b>2,故直线l在y轴上的截距b的取值范围为(-∞,-2-
或b>2,故直线l在y轴上的截距b的取值范围为(-∞,-2-![]() )∪(2,+∞).
)∪(2,+∞).
10.证明:设PQ是过焦点F的弦,M是PQ的中点,l是与F相应的准线,分别过P、Q、M作l的垂线,垂足为P1、Q1、M1,则|MM1|=![]() ||PP1|±|1||=
||PP1|±|1||=![]() ·|
·|![]() ±
±![]() |=
|=![]() |PQ|=
|PQ|=![]() <R,当P、Q位于同一支时,取“+”,否则取“-”,∴以PQ为直径的圆必与准线l相交,且截得的劣弧的弧度数θ=2arccos
<R,当P、Q位于同一支时,取“+”,否则取“-”,∴以PQ为直径的圆必与准线l相交,且截得的劣弧的弧度数θ=2arccos![]() =2arccos
=2arccos![]() 为定值.
为定值.
【素质优化训练】
1.B 2.C
3.A 4.A 5.C
6. ![]() 7.arctan
7.arctan![]() 8.
8. ![]() -y2=1
-y2=1
9.解:题设中的曲线是双曲线中的一段,即![]() -y2=1,(2≤x≤2
-y2=1,(2≤x≤2![]() ,y≥0),A(
,y≥0),A(![]() ,0)是它的右焦点,其右准线为l:x=
,0)是它的右焦点,其右准线为l:x=![]() ,e=
,e=![]() ,设Pn(xn,yn)(2≤xn≤2
,设Pn(xn,yn)(2≤xn≤2![]() ,yn≥0),则|PnA|=e(xn-
,yn≥0),则|PnA|=e(xn-![]() )=
)=![]() xn-2,∴|PnA|min=
xn-2,∴|PnA|min=![]() -2,|PnA|max=3,依题意,可设等差数列首项a1=
-2,|PnA|max=3,依题意,可设等差数列首项a1=![]() -2,第n项an=3=
-2,第n项an=3=![]() -2+(n-1)d,得d=
-2+(n-1)d,得d=![]() (n>1),又
(n>1),又![]() <d<
<d<![]() ,∴
,∴![]() <
<![]() <
<![]() ,得5
,得5![]() -4<n<26-5
-4<n<26-5![]() ,而7<5
,而7<5![]() -4且26-5
-4且26-5![]() <15,∴7<n<15,故n可取最大值为14.
<15,∴7<n<15,故n可取最大值为14.
10.解:(1)过AB的直线方程为bx-ay-ab=0,由点到直线距离公式可得![]() =
=![]() ①,又e=
①,又e=![]() =
=![]() ②,由①、②得b=1,a=
②,由①、②得b=1,a=![]() ,即所求双曲线方程为
,即所求双曲线方程为![]() -y2=1
-y2=1
(2)由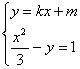 消去y,得(3k2-1)x2+6kmx+3(m2+1)=0,当3k2-1≠0即k≠±
消去y,得(3k2-1)x2+6kmx+3(m2+1)=0,当3k2-1≠0即k≠±![]() 时,△=12(m2-3k2+1)>0,即m2-3k2+1>0 ③,设C(x1,y1),D(x2,y2),CD中点为M(x0,y0).则x0=
时,△=12(m2-3k2+1)>0,即m2-3k2+1>0 ③,设C(x1,y1),D(x2,y2),CD中点为M(x0,y0).则x0=![]() =
=![]() ,y0=kx0+m=-
,y0=kx0+m=-![]() ,因C、D两点都在以A为圆心的同一圆上,∴AM⊥CD,而kAM=
,因C、D两点都在以A为圆心的同一圆上,∴AM⊥CD,而kAM=![]() kCD=k,∴
kCD=k,∴![]() =-
=-![]()
![]() 3k2=4m+1 ④,由④得:4m+1>0m>-
3k2=4m+1 ④,由④得:4m+1>0m>-![]() ⑤,将④代入③:m2-(4m+1)+1>0,得m<0或m>4,综合⑤得m的取值范围为(-
⑤,将④代入③:m2-(4m+1)+1>0,得m<0或m>4,综合⑤得m的取值范围为(-![]() ,0)∪(4,+∞)
,0)∪(4,+∞)
