|
|
学科:数学 |
| 教学内容:椭圆的简单几何性质 |
【基础知识精讲】
1.椭圆![]() +
+![]() =1(a>b>0),范围:椭圆位于直线x=±a和y=±b所围成的矩形里,即|x|≤a,|y|≤b.
=1(a>b>0),范围:椭圆位于直线x=±a和y=±b所围成的矩形里,即|x|≤a,|y|≤b.
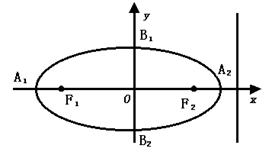
2.对称性:椭圆关于x轴,y轴和原点都是对称的.坐标轴为椭圆的对称轴,原点是椭圆的对称中心,即为椭圆的中心.
3.顶点:椭园与坐标轴的交点为椭圆的顶点为A1(-a,0),A2(a,0),B1(0,b),B2(0,-b)
4.离心率:e=![]() ,(o<e<1),e越接近于1,则椭圆越扁;e越接近于0,椭圆就越接近于圆.
,(o<e<1),e越接近于1,则椭圆越扁;e越接近于0,椭圆就越接近于圆.
5.椭圆的第二定义:平面内的点到定点的距离和它到定直线的距离的比为常数e(0<e<1)的点的轨迹.定点即为椭圆的焦点,定直线为椭圆的准线.
6.椭圆的焦半径公式:设P(x0,y0)是椭圆![]() +
+![]() =1(a>b>0)上的任意一点,F1、F2分别是椭圆的左、右焦点,则|PF1|=a+ex0,|PF2|=a-ex0.
=1(a>b>0)上的任意一点,F1、F2分别是椭圆的左、右焦点,则|PF1|=a+ex0,|PF2|=a-ex0.
7.椭圆的参数方程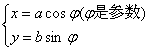
本节学习要求:
椭圆的几何性质内容多.它与直线的位置关系的确定离不开一元二次方程中的判别式及韦达定理.如椭圆中的弦长问题:若直线y=kx+b和二次曲线Ax2+Cy2+Dx+Ey+F=0相交,所得弦长可由下法求之,由两方程中消去y,得ax2+bx+c=0,记△=b2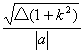 ;若弦过焦点,则用焦半径公式更为简洁.这要求大家针对具体的题目,灵活采用方法计算弦长或与焦半径有关的问题.
;若弦过焦点,则用焦半径公式更为简洁.这要求大家针对具体的题目,灵活采用方法计算弦长或与焦半径有关的问题.
【重点难点解析】
通过“圆的方程”的学习我们知道,圆的几何性质问题用代数的方法解题简便,计算量小的特点,同样,椭圆也有类似的几何性质,那么在学习本节之前要复习椭圆的定义及标准方程,在此基础上来学习椭圆的几何性质,掌握椭圆的性质,标准方程,及椭圆的第二定义.
例1 设直线l过点P(-1,0),倾角为![]() ,求l被椭圆x2+2y2=4所截得的弦长.
,求l被椭圆x2+2y2=4所截得的弦长.
解:直线l的方程为y=![]() x+
x+![]() ,代入椭圆方程,得7x2+12x+2=0,∵△=144-4×7×2=88
,代入椭圆方程,得7x2+12x+2=0,∵△=144-4×7×2=88
∴弦长=![]() =
=![]()
例2 求椭圆![]() +
+![]() =1上的点到直线3x+4y-64=0的最长距离与最短距离.
=1上的点到直线3x+4y-64=0的最长距离与最短距离.
解:设椭圆上的点为(5cosθ,9sinθ),则
d=![]() =
=![]()
=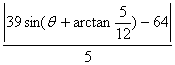
∴dmax=![]()
例3 已知椭圆![]() +
+![]() =1内有一点P(1,-1),F是右焦点,M是椭圆上的动点,求MP+2MF的最小值,并求此时M的坐标.
=1内有一点P(1,-1),F是右焦点,M是椭圆上的动点,求MP+2MF的最小值,并求此时M的坐标.
解:过M作右准线x=4的垂线,垂足为M1,由椭圆第二定义,有![]() =
=![]() ∴2|MF|=|MM1|
∴2|MF|=|MM1|
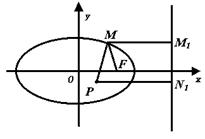
∴|MP|+2|MF|=|MP|+|MM1|
过P作右准线的垂线交椭圆于N,垂足为N1,垂线方程为y=-1.
显然|MP|+|MM1|≥|NP|+|NN1|(当M与N重合时等号成立)而|NP|+|NN1|=|PN1|=3
由方程组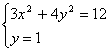 得N(
得N(![]() ,-1)
,-1)
∴|MP|+2|MF|的最小值是3,此时M的坐标是(![]() ,-1)
,-1)
【难题巧解点拨】
例1 P是椭圆方程为![]() +
+![]() =1上的任意一点,F1,F2是椭圆的两个焦点,试求|PF1|·|PF2|的取值范围.
=1上的任意一点,F1,F2是椭圆的两个焦点,试求|PF1|·|PF2|的取值范围.
解:设|PF1|=t,则t∈[a-c,a+c],即t∈[4-![]() ,4+
,4+![]() ]且|PF2|=
]且|PF2|=
∴|PF1|·|PF2|=t(8-t)=-(t-4)2+16 t∈[4-![]() ,4+
,4+![]() ]
]
当t=4时,取最大值为16
当t=4±![]() 时,取最小值为9.
时,取最小值为9.
∴所求范围为[9,16]
例
解:如下图,设|PF1|=t,则|PQ|=t,|F1Q|=![]() t,由椭圆定义有:
t,由椭圆定义有:
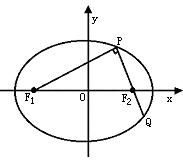
|PF1|+|PF2|=|QF1|+|QF2|=
∴|PF1|+|PQ|+|F1Q|=![]() +2)t=
+2)t=![]() )a
)a
∴|PF2|=![]() -2)a
-2)a
在Rt△PF
∴[(4-2![]() )a]2+[(2
)a]2+[(2![]() -2)a]2=(
-2)a]2=(
∴![]() =9-6
=9-6![]() ∴e=
∴e=![]() =
=![]() -
-![]()
例3 已知P是椭圆![]() +
+![]() =1(a>b>0)上的一点,F
=1(a>b>0)上的一点,F
解:(利用椭圆第二定义求解)
∵点P到两准线的距离分别是6和12
∴2·![]() =6+12 即a2=
=6+12 即a2=
由椭圆第二定义知,e=![]() =
=![]()
∵d1=6,d2=12 ∴|PF1|=6e,|PF2|=12e
又∵PF1⊥PF2 ∴|PF1|2+|PF2|2=|F
∴36e2+144e2=![]() ∴a2=45
∴a2=45
又a2=
∴所求椭圆的方程的![]() +
+![]() =1
=1
例4 在椭圆3x2+4y2=12上,是否存在相异的两点A、B关于直线y=4x+m对称并说明理由.
解:设A(x1,y1),B(x2,y2),AB的中点M(x0,y0)
直线AB:y=-![]() x+t,将AB的方程代入椭圆的方程消去y得,13x2-8tx+16t2-48=0
x+t,将AB的方程代入椭圆的方程消去y得,13x2-8tx+16t2-48=0
∴△=(-8t)2-4×13×(16t2-48)>0
∴-![]() <t<
<t<![]() ①且x1+x2=
①且x1+x2=![]() t
t
又AB的中点M在直线y=4x+m上,
∴![]() t=4×
t=4×![]() t+m ∴t=-
t+m ∴t=-![]() m
m
代入①式得:
-![]()
![]() <m<
<m<![]()
![]()
解法二:设A(x1,y1),B(x2,y2)是椭圆上关于直线l:y=4x+m对称的两点,则
![]() +
+![]() =1 ①
=1 ① ![]() +
+![]() =1 ②
=1 ②
①-②得![]() +
+![]() =0
=0
∴![]() =
=![]()
而KAB=![]() =-
=-![]()
故有![]() =-
=-![]()
设AB的中点为(x,y),则有x1+x2=2x,y1+y2=2y
代入即得AB中点的轨迹方程为y=3x.
由![]()
由于AB的中点在椭圆内部
∴![]() +
+![]() <1
<1![]() m2<
m2<![]()
![]() -
-![]()
![]() <m<
<m<![]()
![]()
故当m∈(-![]()
![]() ,
,![]()
![]() )时,椭圆C上有不同的两点关于直线对称.
)时,椭圆C上有不同的两点关于直线对称.
例5 椭圆![]() =1上不同三点A(x1,y1),B(4,
=1上不同三点A(x1,y1),B(4,
![]() ),C(x2,y2)与焦点F(4,0)的距离成等差数列.
),C(x2,y2)与焦点F(4,0)的距离成等差数列.
(1)求证:x1+x2=8
(2)若线段AC的垂直平分线与x轴的交点为T,求直线BT的斜率k.
解:由题知a=5,b=3,c=4.
(1)由椭圆的第二定义知:
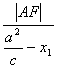 =
=![]()
![]() |AF|=a-
|AF|=a-![]() x1=5-
x1=5-![]() x1
x1
同理有|CF|=5-![]() x2
x2
∵|AF|+|CF|=2|BF|
且|BF|=![]()
∴(5-![]() x1)+(5-
x1)+(5-![]() x2)=
x2)=![]()
即x1+x2=8
(2)∵线段AC的中点为(4,![]() )
)
∴它的垂直平分线方程为y-![]() =
=![]() (x-4)
(x-4)
又点T在x轴上,设其坐标为(x0,0),代入上式得,x0-4=![]() ①
①
点A(x1,y1),B(x2,y2)都在椭圆上
∴y21=![]() (25-x21),y22=
(25-x21),y22=![]() (25-x22)
(25-x22)
∴y21-y22=-![]() (x1+x2)(x1-x2)
(x1+x2)(x1-x2)
将此式代入①并利用x1+x2=8得
x0-4=-![]()
∴kBT=![]() =
=![]()
【命题趋势分析】
1.熟练掌握椭圆的第二定义,两种形式的标准方程及几何性质,运用它们及参数间的关系解决相关问题.
2.必要时,椭圆方程可设为mx2+ny2=1(m>0,n>0),这样计算简洁,还可避免对焦点位置的讨论.
3.遇到弦的中点问题时,常用点差法.
例1 椭圆![]() =1的焦点为F1,F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1,F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
A.7倍 B.5倍 C.4倍 D.3倍
解:设F1(-3,0),e=![]() ,P(x0,y0)
,P(x0,y0)
∵线段PF1的中点的横坐标为0,∴![]() =0 即x0=3
=0 即x0=3
∴|PF1|=a+ex0=2![]() +
+![]() ×3=
×3=![]()
![]()
∴|PF2|=2a-|PF1|=4![]() -
-![]()
![]() =
=![]()
∴|PF1|=7|PF2| 故选A
例2 设椭圆的中心是坐标原点,长轴在x轴上,离心率e=![]() ,已知点P(0,
,已知点P(0,![]() )到这个椭圆上的点的最远距离为
)到这个椭圆上的点的最远距离为![]() ,求这个椭圆方程,并求椭圆上到P的距离等于
,求这个椭圆方程,并求椭圆上到P的距离等于![]() 的点的坐标.
的点的坐标.
解:设所求椭圆方程为![]() +
+![]() =1(a>b>0)
=1(a>b>0)
由e2=![]() =
=![]() =1-
=1-![]() 和e=
和e=![]() 得a=2b
得a=2b
设椭圆上的点(x,y)到P点的距离为d,则
d2=x2+(y-![]() )2=a2(1-
)2=a2(1-![]() )+y2-3y+
)+y2-3y+![]()
=-3(y+![]() )2+4b2+3 (-b≤y≤b)
)2+4b2+3 (-b≤y≤b)
若b<![]() 时,则当y=-b时,d2(从而d)有最大值,由题设得(
时,则当y=-b时,d2(从而d)有最大值,由题设得(![]() )2=(b+
)2=(b+![]() )2,由此得b=
)2,由此得b=![]() -
-![]() >
>![]() 与b<
与b<![]() 矛盾.
矛盾.
若b≥![]() 时,当y=-
时,当y=-![]() 时,d2有最大值,从而d有最大值,有(
时,d2有最大值,从而d有最大值,有(![]() )2=4b2+3,∴b=1,a=2
)2=4b2+3,∴b=1,a=2
∴所求椭圆方程为![]() +y2=1,椭圆上的点(-
+y2=1,椭圆上的点(-![]() ,-
,-![]() ),点(
),点(![]() ,-
,-![]() )到P点的距离都是
)到P点的距离都是![]() .
.
说明:本题体现了数学的转化与函数思想,本题关键是讨论距离函数d2=-3(y+![]() )2+4b2+3在区间[-b,b]上的最值,二次函数在区间上的最值问题要就对称轴与区间的关系来讨论.
)2+4b2+3在区间[-b,b]上的最值,二次函数在区间上的最值问题要就对称轴与区间的关系来讨论.
例3 已知椭圆的中心在原点O,焦点在坐标轴上,直线y=x+1与该椭圆相交于P和Q,且OP⊥OQ,|PQ|=![]() .求椭圆方程.
.求椭圆方程.
分析 设P(x1,y1),Q(x2,y2,)由OP⊥OQ知x1x2+y1y2=0,再结合弦长公式与韦达定理求解.
解:设椭圆的方程为![]() +
+![]() =1(a>0,b>0,a>b或a<b),点P、Q的坐标别为P(x1,y1),Q(x2,y2).
=1(a>0,b>0,a>b或a<b),点P、Q的坐标别为P(x1,y1),Q(x2,y2).
由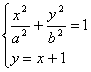 消去y得
消去y得
(a2+b2)x2+2a2x+a2-a2b2=0,
当△=(2a2)2-4(a2+b2)(a2-a2b2)>0时由韦达定理得
x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
且y1=x1+1,y2=x2+1,
∵OP⊥OQ,∴![]() ·
·![]() =-1,即y1y2+x1x2=0,
=-1,即y1y2+x1x2=0,
∴(x1+1)(x2+1)+x1x2=0,
∴2x1x2+(x1+x2)+1=0, ①
又|PQ|=![]() ,由弦长公式有:
,由弦长公式有:
![]() |x2-x1|=
|x2-x1|=![]() ,
,
∴2[(x1+x2)2-4x1x2]=![]() ,
,
∴4(x1+x2)2-16x1x2-5=0 ②
解由①、②组成的方程组得
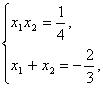 或
或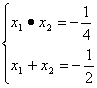
∴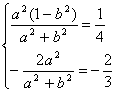 ,或
,或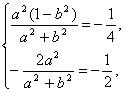
解得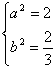 或
或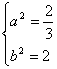
故所求椭圆方程为![]() +
+![]() =1或
=1或![]() +
+![]() =1
=1

【同步达纲练习】
A级
一、选择题
1.椭圆![]() +
+![]() =1与
=1与![]() +
+![]() =k(a>b>0,k>0)一定具有相同的( )
=k(a>b>0,k>0)一定具有相同的( )
A.长轴 B.焦点 C.离心率 D.顶点
2.离心率为![]() ,且过点(2,0)的椭圆标准方程为( )
,且过点(2,0)的椭圆标准方程为( )
A. ![]() +y2=1 B.
+y2=1 B.
![]() +y2=1或x2+
+y2=1或x2+![]() =1
=1
C. x2+![]() =1 D.
=1 D.
![]() +y2=1或
+y2=1或![]() +
+![]() =1
=1
3.若方程![]() +
+![]() =1表示焦点在y轴上的椭圆,则实数m的取值范围是( )
=1表示焦点在y轴上的椭圆,则实数m的取值范围是( )
A.(-16,25) B.(
![]() ,25) C.(-16,
,25) C.(-16,![]() ) D.(
) D.(
![]() ,+∞)
,+∞)
4.若圆(x-a)2+y2=9与椭圆![]() +
+![]() =1有公共点,则实数a的取值范围是( )
=1有公共点,则实数a的取值范围是( )
A.(-∞,+∞) B.[-6,6] C.[-![]() ,
,![]() ] D.
] D.![]()
5.若椭圆的两个焦点三等分两条准线间的距离,则椭圆的离心率为( )
A.3 B.![]() C.
C.![]() D.
D.![]()
二、填空题
6.椭圆![]() +
+![]() =1的离心率e=
=1的离心率e=![]() ,则实数m的值为
.
,则实数m的值为
.
7.若方程![]() +
+![]() =-1表示椭圆,则实数k的取值范围是
.
=-1表示椭圆,则实数k的取值范围是
.
8.若椭圆的长轴长、短轴长,焦距依次成等差数列,则其离心率e= .
三、解答题
9.已知椭圆![]() +
+![]() =1上的点P到其右焦点的距离是长轴两端点到右焦点的距离的等差中项,求P点坐标.
=1上的点P到其右焦点的距离是长轴两端点到右焦点的距离的等差中项,求P点坐标.
10.已知P是椭圆![]() +
+![]() =1上的点,且∠F1PF2=90°,求△F1PF2的面积.
=1上的点,且∠F1PF2=90°,求△F1PF2的面积.
AA级
一、选择题
1.不论k为何值,直线y=kx+1与焦点在x轴上的椭圆![]() +
+![]() =1有公共点,则实数m的范围是( )
=1有公共点,则实数m的范围是( )
A.(0,1) B.(0,7) C.[1,7] D.(1,7]
2.椭圆的两个焦点和中心将两准线间的距离四等分,则一焦点与短轴两端点连线的夹角为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]() π
π
3.已知F1、F2是椭圆![]() +
+![]() =1(a>b>0)的两个焦点AB是过F1的弦,则△ABF2的周长是( )
=1(a>b>0)的两个焦点AB是过F1的弦,则△ABF2的周长是( )
A.2a B.4a C.8a D.2a+2b
4.已知(0,-4)是椭圆3kx2+ky2=1的一个焦点,则实数k的值是( )
A.6 B.
![]() C.24 D.
C.24 D.![]()
5.以椭圆的右焦点F2为圆心作圆,使这圆过椭圆的中心,且交椭圆于M点,若直线MF1是圆F2的切线,则椭圆的离心率是( )
A. ![]() -1 B.2-
-1 B.2-![]() C.
C.
![]() D.
D.
![]()
二、填空题
6.以椭圆的两个焦点为直径端点的圆交椭圆于四个点,若顺次连接四个点及两个焦点恰好组成一个正六边形,则椭圆的离心率e= .
7.已知F1F2是椭圆两焦点,P是椭圆上一点,△PF1F2满足∠PF1F2:∠PF2F1:∠F1PF2=1∶2∶3,则此椭圆的离心率e=
8.已知A(1,1) B(2,3),椭圆C:x2+4y2=4a2,如果椭圆C和线段AB有公共点,则正数a的取值范围是 .
三、解答题
9.已知A、B是椭圆![]() +
+![]() =1上的两点,F2是椭圆的右焦点,若|AF2|+|BF2|=
=1上的两点,F2是椭圆的右焦点,若|AF2|+|BF2|=![]() a,AB中点到椭圆左准线距离为
a,AB中点到椭圆左准线距离为![]() ,求椭圆方程.
,求椭圆方程.
10.设椭圆![]() +
+![]() =1(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
=1(a>b>0)的左顶点为A,若椭圆上存在一点P,使∠OPA=![]() ,求椭圆离心率的取值范围.
,求椭圆离心率的取值范围.
【素质优化训练】
一、选择题
1.已知M为椭圆上一点,F1F2是两焦点,且∠MF1F2=2α,∠MF2F1=α(α≠0),则椭圆的离心率是( )
A.1-2sinα B.1-sin2α C.1-cos2α D.2cosα-1
2.椭圆2x2+y2=1上的点到直线y=![]() x-4的距离的最小值是( )
x-4的距离的最小值是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
3.已知F是椭圆![]() +
+![]() =1(a>b>0)的一个焦点,PQ是过其中心的一条弦,则△FQP面积的最大值是( )
=1(a>b>0)的一个焦点,PQ是过其中心的一条弦,则△FQP面积的最大值是( )
A.![]() ab B.ab C.ac D.bc
ab B.ab C.ac D.bc
4.已知椭圆![]() +
+![]() =1(a>b>0)的离心率等于
=1(a>b>0)的离心率等于![]() ,若将此椭圆绕右焦点按逆时针方向旋转
,若将此椭圆绕右焦点按逆时针方向旋转![]() 后,新位置的椭圆有一条准线方程是y=
后,新位置的椭圆有一条准线方程是y=![]() ,则原椭圆方程是( )
,则原椭圆方程是( )
A.![]() +
+![]() =1 B.
=1 B.
![]() +
+![]() =1
=1
C.![]() +
+![]() =1 D.
=1 D.
![]() +
+![]() =1
=1
5.椭圆![]() +
+![]() =1的一个焦点为F1,点P在椭圆上,若线段PF1的中点M在y轴上,则M的纵坐标是( )
=1的一个焦点为F1,点P在椭圆上,若线段PF1的中点M在y轴上,则M的纵坐标是( )
A.±![]() B.±
B.±![]() C.±
C.±![]() D.±
D.±![]()
二、填空题
6.已知圆柱底面的直径为2k,一个与底面成30°角的平面截这个圆柱,则截面上的椭圆的离心率是
7.已知P是椭圆![]() +
+![]() =1(a>b>0)上的点,且∠F1PF2=θ,则△F1PF2的面积是
=1(a>b>0)上的点,且∠F1PF2=θ,则△F1PF2的面积是
8.点P(0,1)到椭圆![]() +y2=1上点的最大距离是
.
+y2=1上点的最大距离是
.
三、解答题
9.已知椭圆长轴|A1A2|=6,|F1F2|=4![]() ,过椭圆焦点F1作一直线,交椭圆于M、N两点,设∠F2F1M=α(0≤α≤π),问当α取何值时,|MN|等于椭圆的短轴长.
,过椭圆焦点F1作一直线,交椭圆于M、N两点,设∠F2F1M=α(0≤α≤π),问当α取何值时,|MN|等于椭圆的短轴长.
10.已知椭圆![]() +
+![]() =1(a>b>0)与x轴交于AB两点,F1F2为焦点.
=1(a>b>0)与x轴交于AB两点,F1F2为焦点.
(1)过一焦点F2作垂直于长轴的弦MN,求∠AMB的大小范围
(2)若椭圆上有一点P,使得∠APB=120°,求P点的纵坐标,并求椭圆离心率满足什么条件时,这样的点P才存在.
【生活实际运用】
要把一个边长分别为52cm和30cm的矩形板锯成椭圆形,使它的长轴和短轴长分别为52cm和30cm用简便的方法在木板上画出这个椭圆的草图.

参考答案:
【同步达纲练习】
A级
1.C 2.D
3.B 4.B 5.D
6. ![]() 或
或![]() 7.3<k<5且k≠4 8.
7.3<k<5且k≠4 8. ![]() 9.(0,2)或(0,-2) 10.4
9.(0,2)或(0,-2) 10.4
AA级
1.C 2.C
3.B 4.D 5.A
6. ![]() -1 7.
-1 7.![]() -1 8.[
-1 8.[![]() ,
, ![]() ] 9.x2+
] 9.x2+![]() y2=1
10.
y2=1
10.![]() <e<1
<e<1
【素质优化训练】
1.D 2.D
3.D 4.C 5.A
6.![]() 7.b2tan
7.b2tan![]() 8.2 9.α=
8.2 9.α=![]() 或
或![]() π 10.(1)
π 10.(1) ![]() <∠AMB<π-arccot2 (2)e∈[
<∠AMB<π-arccot2 (2)e∈[![]() ,1]
,1]
