椭圆及其标准方程

	学科：数学
	教学内容：椭圆及其标准方程

【基础知识精讲】

1.椭圆的定义：平面内与两个定点F₁、F₂的距离之和等于常数(大于｜F₁F₂｜)的点的轨迹叫做椭圆，这两个定点叫做椭圆的焦点，两焦点间的距离叫做焦距.

注意：定义中的常数用2a表示，｜F₁F₂｜用2c表示，当2a＞2c＞0时，轨迹为椭圆，当2a=2c时，轨迹为线段F₁F₂；当2a＜2c时，无轨迹.这样，椭圆轨迹一定要有2a＞2c这一条件.另外，应用定义来求椭圆方程或解题时，往往比较简便.

2.椭圆的标准方程

当焦点在x轴上时：+=1(a＞b＞0)

当焦点在y轴上时：+=1(a＞b＞0)

注意：(1)三个量之间的关系：a²=b²+c²

(2)由x²,y²的分母大小确定焦点在哪条坐标轴上，x²的分母大，焦点就在x轴上，y²的分母大，焦点就在y轴上.

(3)在方程Ax²+By²=C中，只有A、B、C同号时，才可能表示椭圆方程.

(4)当且仅当椭圆的中心在原点，其焦点在坐标轴上时，椭圆的方程才具有标准形式.

本节学习方法：

1.求椭圆方程常用待定系数法，定义法，参数法，轨迹法等.

2.利用椭圆的定义和标准方程解决有关问题，一般都转化成某些数值的确定，而这些数值的确定可通过列方程，解方程去解决.

【重点难点解析】

同学们学习“椭圆”应与学习“圆”一样，遵循渐近性，逻辑性.注重数形结合，主要掌握椭圆的定义及其标准方程，需要大家学习本节时，先复习求曲线方程的方法，进行反复的再思考，再分析再理解.

例1　求与椭圆+=1共焦点，且过点M(3，-2)的椭圆方程.

解法一：(待定系数法)由已知椭圆方程+ =1得C²=9-4=5，且焦点在x轴上，设所求椭圆方程为+=1

又∵点M(3，-2)在椭圆上

∴+=1，得a⁴-18a²+45=0

∴a²=15或a²=3＜5=C²(舍)

∴所求椭圆方程为+=1

解法二：(定义法)椭圆两焦点为F₁(-，0)，F₂(，0)，点M(3，-2)到这两个焦点距离之和是2a，即

2a=｜M₁F₁｜+｜M₁F₂｜= +=2

∴a²=15　b²=a²-c²=15-5=10

∴所求椭圆方程为+=1

例2　已知椭圆的中心在原点，以坐标轴为对称轴，且经过两点P₁(，1)，P₂(-，-)，求椭圆的方程.

解：设椭圆方程为mx²+ny²=1,(m＞0，n＞0)

由题意有

解得m=，n=

∴所求椭圆方程为+=1

说明：设椭圆方程为mx²+ny²=1(m＞0，n＞0)可免讨论焦点的位置，而且计算简便.

例3　已知点P在以坐标轴为对称轴的椭圆上，点P到两焦点的距离分别为和，过P作焦点所在轴的垂线恰好过椭圆的一个焦点，求椭圆方程.

解：设两个焦点为F₁F₂，且｜PF₁｜=，｜PF₂｜=

由椭圆定义知2a=｜PF₁｜+｜PF₂｜=2　 ∴a=

而｜PF₁｜＞｜PF₂｜知PF₂与焦点所在的对称轴垂直.

∴Rt△PF₂F₁中，sin∠PF₁F₂==

∴∠PF₁F₂=

2C=｜PF₁｜cos=

∴b²=a²-c²=

故所求方程为+y²=1或x²+=1

3.(代入法)与椭圆有关的轨迹问题：常用的方法有定义法，坐标转移法，交轨法，点差法.

例4　已知圆C₁：x²+y²+4x-12=0与圆C₂:x²+y²-4x=0，动圆C与C₁相内切，且与C₂相外切，求动圆圆心的轨迹方程.

解：圆C₁与C₂的标准方程是

(x+2)²+y²=16，(x-2)²+y²=4

圆心分别为C₁(-2，0)，C₂(2，0)

设动圆P的圆心为P，半径为r，有

｜PC₁｜=4-r,｜PC₂｜=2+r

∴｜PC₁｜+｜PC₂｜=6＞｜C₁C₂｜=4

∴P点在椭圆上运动，又2a=6，2c=4，∴b²=a²-c²=5

∴P的轨迹为+=1(在已知圆C₁内)

【难题巧解点拨】

例1　已知MN是椭圆+=1(a＞b＞0)中垂直于长轴的动弦，AB是椭圆长轴的两端点，求直线MA与NB的交点P的轨迹方程.

解：设M、N的坐标为M(x₀,y₀)，N(x₀,-y₀)，又A(-a,0),B(a,0)

所以直线AM的方程为y= (x+a)　　　　　　　①

直线BN的方程为：y=　　　　　　　　②

①×②得：y²=(x²-a²) 　　　　　　　　　　③

∵点M(x₀,y₀)在椭圆上，∴b²x²₀+a²y²₀=a²b²

∴x²₀-a²=-y₀²,代入得③得：y²=(x²-a²)

∴交点P的轨迹方程为-=1

例2　已知椭圆+y²=1

(1)求斜率为2的平行弦的中点轨迹方程

(2)过A(2，1)引椭圆的割线，求截得的弦中点轨迹方程

(3)求过点P(，)，且被P平分的弦所在的直线方程.

解：(点差法)设弦的两端点分别为M(x₁,y₁)

N(x₂,y₂)、MN的中点为P(x,y)，则

x²₁+2y²₁=2，x²₂+2y²₂=2,两式相减并除以(x₂-x₁)得：

x₁+x₂+2(y₁+y₂) =0

而x₁+x₂=2x,y₁+y₂=2y

∴x+2y· =0　  (*)

(1)将=2代入(*)式得所求的轨迹方程为

x+4y=0(椭圆内部分)

(2)将=代入(*)式，得所求的轨迹方程为x²+2y²-2x-2y=0(椭圆内部分)

(3)将x₁+x₂=1,y₁+y₂=1代入(*)式，得=-

∴所求的直线方程为2x+4y-3=0

例3　已知中心在原点，一焦点为F(0，)的椭圆被直线l:y=3x-2截得弦的中点横坐标为，求椭圆方程.

解：∵C= ，∴a²=b²+50

∴可设椭圆方程为+=1

把直线y=3x-2代入椭圆方程整理得

10(b²+5)x²-12b²x-b⁴-46b²=0

∴x₁+x₂=

又∵=

∴12b²=10b²+50

解得b²=25　a²=75

∴所求的椭圆方程为+=1

例4　已知P为椭圆+=1上的一点，F₁F₂是椭圆上的两焦点，∠F₁PF₂=60°，求△F₁PF₂的面积.

解：∵=｜PF₁｜·｜PF₂｜sin∠F₁PF₂

∴只需求｜PF₁｜·｜PF₂｜即可

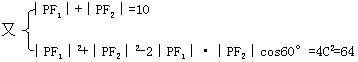
解得｜PF₁｜·｜PF₂｜=12

∴=×12×=3

例5　　已知方程2(k²-2)x²+k²y²+k²-k-6=0表示椭圆，求实数k的取值范围.

解：结合椭圆的变形方程式a²y²+b²x²-a²b²=0从而有：

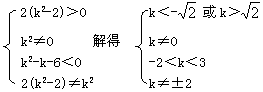
∴k∈(-2，-)∪(，2)∪(2，3)

例6　　△ABC的三边a＞b＞c，且a+c=2b，｜AC｜=2,求顶点B的轨迹.

解：以AC的中点为坐标原点建立坐标系，则A(-1，0)，C(1，0)，又a+c=2b=4

由椭圆的定义知B点在椭圆上运动.

∵a＞b＞c，且A、B、C三点不共线

∴B点的轨迹方程是椭圆+=1，在y轴左侧的部分，但要去掉点(-2，0)，(0，)，(0，-)

【知识探究学习】

问题：如何用尺规作图法作椭圆的大致示意图.

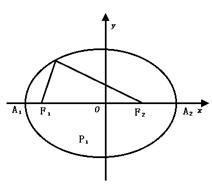
提示：由椭圆的定义作图，建立如图的坐标系，取｜OF₁｜=｜OF₂｜=C,｜OA₁｜=｜OA₂｜=a

在F₁F₂间任取一点P₁，以｜P₁A₁｜为半径，以F₁为圆心画弧；以F₂为圆心，以｜P₁A₂｜为半径画弧，两弧的交点即在所求椭圆上.用同样的方法去F₁F₂间取一系列点，最后用圆滑曲线连起来即可.请同学们证明.

【典型热点考题】

例1　求椭圆+=1上一动点P到直线3x+8y+72=0距离的最大值及最小值.

分析　常规思路是设P(x₀,y₀)是椭圆上的点，其到直线的距离为d=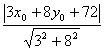,怎样求d的最值呢?这样计算较为麻烦!换一个角度思考，假设椭圆上点P(x₀,y₀)到直线的距离最大或最小，过P作已知直线的平行线l′，则l′与椭圆的位置关系怎样呢?应相切，否则P一定不是距离的最大或最小.

解：设与直线3x+8y+72=0平行直线为3x+8y+t=0，由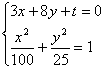消去y得：25x²+6tx+(t²-1600)=0

令△=0即4［9t²-25(t²-1600)］=0

∴t=±50

当t=50时，直线3x+8y+50=0与直线3x+8y+72=0间的距离是d₁=

当t=-50时，直线3x+8y-50=0与直线3x+8y+72=0间的距离是d₂=

∴最大距离为，最小距离为

例2　在面积为1的△PMN中，tan∠PMN= ，tan∠MNP=-2，建立适当的坐标系求出以M、N为焦点且过点P的椭圆方程.

分析　以MN所在直线为x轴，线段MN的垂直平分线为y轴，建立直角坐标系如下图.

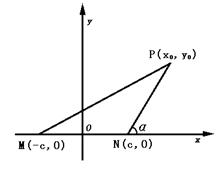
设所求椭圆方程为+=1(a＞b＞0),分别设M、N、P点坐标为(-c，0)，(c,0)和(x₀,y₀).

∵tanα=tan(π-∠MNP)=2

由题设知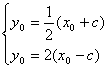

解得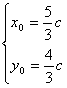

即　P(c, c)

在△MNP中，｜MN｜=2c,MN上的高为c

∵S_△MNP=·2c· c=1

∴c=即P(，)

∵点P在椭圆上且a²=b²+c²

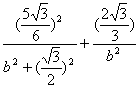∴=1

解得　b²=3或b²=-(舍去)

∴a²=b²+c²=

故所求椭圆方程为：x²+=1

【同步达纲练习】

A级

一、选择题

1.椭圆的两个焦点分别是F₁(-8，0)和F₂(8，0)，且椭圆上一点到两个焦点的距离之和是20，则此椭圆方程是(　　)

A.3x²+=1　 　　 　　　　　　B.+=1

C.+  =1　　　　　　　　 D.  +=1

2.与椭圆+=1共焦点，且过点P(3，-2)的椭圆方程是(　　)

A.  +=1　　　　　　　　　B. +=1

C.+ =1　　　　　　　　　 D. +=1

3.椭圆+=1的焦距是2，则m的值是 (　　)

A.5　　　　　　 B.8　　　　　　 C.5或3　　　　　　 D.20

4.过椭圆+ =1左焦点F₁引直线l交椭圆于A、B两点，F₂是椭圆的右焦点，则△ABF₂的周长是(　　)

A.16　　　　　　　　B.18　　　　　　　　C.20　　　　　　　　　　D.不能确定

5.以两条坐标轴为对称轴的椭圆过点P(，-4)和Q(-，3)，此椭圆的方程是(　　)

A. +y²=1　　　　　　　　　　 B.x²+=1

C.+y²=1或x²+=1　　　　　 D.非A、B、C答案

二、填空题

6.椭圆以两条坐标轴为对称轴，一个顶点是(0，13)，另一个顶点是(-10，0)，则焦点坐标是　　　　　　　　　 　　　　.

7.椭圆以坐标轴为对称轴，长、短半轴之和为10，焦距为4，则椭圆方程为　　　　  .

8.P点在椭圆+=1上，F₁，F₂是椭圆的焦点，若PF₁⊥PF₂，则P点的坐标是　　　　 .

三、解答题

9.椭圆+=1(a＞b＞0)的两个焦点及其与坐标轴的一个交点正好是一个等边三角形的三个顶点，且椭圆上的点到焦点距离的最小值为，求椭圆的方程.

10.已知椭圆+=1上的点P到其右焦点的距离是长轴两端点到右焦点的距离的等差中项，求P点坐标.

AA级

一、选择题

1.在△ABC中，A(-1，0)，C(1，0)，且｜BC｜、｜CA｜、｜AB｜成公差为负的等差数列，则顶点B的轨迹方程为(　　)

A. +=1　　　　　　　　　　　 B. +=1(x＞0)

C. + =1(-2＜x＜0＝　　　　　 D. +=1(x＜0)

2.椭圆的焦点为(-2，0)和(2，0)，且椭圆过点(，-)，则椭圆方程是(　　)

A. +=1　　　　　　　　　　　 B. +=1

C. +=1　　　　　　　　　　　 D. + =1

3.P是椭圆+=1上的点，它到左焦点的距离等于它到右焦点距离的2倍，则P点的坐标是(　　)

A.(1，)　　　　　　　　　　　 B. ( ，)

C.(1，±)　　　　　　　　　　 D. (,±)

4.若关于x,y的方程x²sinα-y²cosα=1所表示的曲线是椭圆，则方程(x+cosα)²+(y+sinα)²=1所表示的圆心在(　　)

A.第一象限　　　B.第二象限　　　C.第三象限　　　D.第四象限

5.椭圆的对称轴是坐标轴，O为坐标原点，A是一个顶点，若椭圆的长轴长是6，且cos∠OFA=则椭圆的方程是(　　)

A. +=1　　　　　　　　　　　 B. +=1

C. +=1或+=1　　　　　 D. +=1或+=1

二、填空题

6.在周长为16的△ABC中，若B、C的坐标分别是(-3，0)和(3，0)，则点A的轨迹方程是　　　　　　　　.

7.直线x-y-m=0与椭圆+y²=1相切，则m的值是　　　　　　　 .

8.椭圆的一个焦点到长轴两端点的距离之比是1∶4，短轴长为8，则椭圆的标准方程是

　　　　　　　

三、解答题

9.椭圆+=1的内接矩形的长与宽的比是3∶2，求矩形的面积.

10.椭圆+=1(a＞b＞0)上存在一点P，使得OP⊥AP(O为原点，A为长轴端点)，求证：a＞b.

【素质优化训练】

一、选择题

1.已知椭圆+=1，F₁F₂是它的两个焦点，P是这个椭圆上任意一点，那么当｜PF₁｜·｜PF₂｜取最大值时，P、F₁、F₂三点(　　)

A.共线　　　　　　　　　　　　　B.组成一个正三角形

C.组成一个等腰直角三角形　　　　　　D.组成一个锐角三角形

2.A、B分别是x轴，y轴正方向上的点，F为OA上的点，∠OFB=30°，当S_△ABF=2-，那么以OA为长半轴，OB为短半轴，F为焦点的椭圆方程是(　　)

A. +=1　　　　　　　　　 B. +=1

C. +=1　　　　　　　　　 D. +=1

3.椭圆ax²+by²=-ab(a＜b＜0＝的焦点坐标是(　　)

A.(±,0)　　　　　　　　 B.(±,0)

C.(0,±)　　　　　　　　 D.(0,±)

4.B₁、B₂是椭圆短轴的两端点，过左焦点F₁作长轴的垂线交椭圆于P，若｜F₁B₂｜是｜OF₁｜和｜B₁B₂｜的比例中项，则的值是(　　)

A.　　 　　 B. 　　　　 C. 　　　　 D.

5.若M(x,y)适合arcsin+arccos=π，则点M轨迹方程是(　　)

A.  +=1(x≠0)　　　　　　　　B. +=1(x≤0,y≥0)

C. +=1(y≠0)　　　　　　 D. +=1(x≥0,y≤0)

二、填空题

6.椭圆+=1上各点与其左焦点所连线段中点的轨迹方程为　　　　　　　 .

7.若B(-8，0)，C(8，0)为△ABC的两顶点，AC和AB两边上的中线之和是30，则△ABC的重心轨迹的标准方程是　　　　　　　 .

8.已知椭圆+=1的两焦点F₁，F₂，以F₁F₂为直径的圆与椭圆相交于其中一个交点P，则△F₁PF₂的面积是　　　　　　　 .

三、解答题

9.已知椭圆+=1(a＞b＞0),A、B是椭圆上的两点，线段AB的垂直平分线与x轴相交于点P(x₀,O),证明：-＜x₀＜

10.P为椭圆+=1(a＞b＞0)上一点，过P作圆x²+y²=b²的两条切线PA、PB，A、B为切点，直线AB分别交x,y轴于M、N，求△OMN面积的最小值.

【生活实际运用】

1.取一条一定长的细绳，把它的两端固定在画图板上的F₁和F₂两点，当绳长大于F₁和F₂的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，就可画一个椭圆.

2.一束光线垂直于一个墙面，将一块圆形纸板置于光源与墙面之间，墙面会出现纸板的影子，变化纸板与光线的角度，影子的形状也会发生变化，观察这些影子会出现哪些不同的形状.

参考答案：

A级

1.C　2.C  3.C　4.C　5.B  6.(0，-)　(0，)　7. +=1或+=1　8.(3，4)，(3，-4)，(-3，4)，(-3，-4)　9. +=1　10.(0，2)或(0，-2)

AA级

1.C　2.B  3.D　4.D　5.D  6. +=1(y≠0)　7.±　8. +=1或+=1　9. 或

10.设P(x₀,y₀),A(a,0),则y²₀= (a²-x²₀)，由OP⊥AP得y²₀=x₀(a-x₀),解得x₀=，不妨设P在第一象限，则0＜x₀＜a，即0＜＜a,得a＞b.

【素质优化训练】

1.B　2.D  3.D　4.B　5.D  6. +y²=1  7. +=1　8.4　9.略　10.S_△OMNmin=