|
|
学科：数学 |
| 教学内容：圆的方程 |
【基础知识精讲】
1.圆的方程：三个独立条件确定一个圆，根据已知条件可用待定系数法求圆的方程时，如果已知圆心或半径，或圆心到某直线的距离，通常用圆的标准方程，如果已知圆经过某些点，通常可用一般式.学习圆的方程，要正确掌握几何性质.和对应条件：
(1)过原点的圆x2+y2+Dx+Fy=0或(x-a)2+(y-b)2=a2+b2
(2)圆心在x轴上的圆x2+y2+Dx+F=0(D2
(3)圆心在y轴上的圆x2+y2+Ey+F=0(E2
(4)圆心在x轴上，且与y轴相切的圆x2+y2+px=0，或(x-a)2+y2=a2
(5)圆心在y轴上，且与x轴相切的圆x2+y2+Ey=0或x2+(y-b)2=b2
2.直线和圆的位置关系
直线与圆心位置关系的判断方法有两种：
(1)判别式法(代数法)：将直线和圆的方程联立得到一个关于x、y的二元二次方程组，消去y(或x)得到一个关于x(或y)的一元二次方程，则
△＞0
直线和圆相交(有两个公共点)
△=0直线和圆相切(有一个公共点)
△＜0直线和圆相离(无公共点)
若涉及到弦长等问题，则可结合韦达定理进一步解决.
(2)几何法：设圆心到直线的距离为d,圆的半径为r，则
d＜r直线与圆相交(有两个公共点)
d=r直线与圆相切(有一个公共点)
d＞r直线与圆相离(无公共点)
若涉及到弦长等问题，则可抓住圆心到直线的距离d、圆的半径r、弦长的一半l三者组成的直角三角形解决.
3.圆与圆的位置关系，设两个圆的半径分别为R、r，圆心距为d,则
(1)两个圆外离d＞R+r
(2)两个圆外切d=R+r
(3)两个圆相交｜R-r｜＜d＜R+r
(4)两个圆内切d=｜R-r｜
(5)两个圆内含0≤d＜｜R-r｜
4.圆系方程：
(1)过直线l:Ax+By+C=0和圆x2+y2+Dx+Ey+F=0的公共点的圆的方程可以写作(Ax+By+C)+λ(x2+y2+Dx+Ey+F)=0；
(2)过圆C1：x2+y2+D1x+E1y+F2=0和圆C2：x2+y2+D2x+E2y+F2=0的公共点的圆(除C2外)的方程可以写成(x2+y2+D1x+E1y+F1)+λ(x2+y2+D2x+E2y+F2)=0.
特殊地，令λ=-1即得过两个圆的公共点的直线的方程：(D1-D2)x+(E1-E2)y+(F1-F2)=0.
5.圆的参数方程：圆心为(a,b)、半径为r的圆的参数方程为
6.应用代入法、几何法、参数法等方法求与圆有关的轨迹问题.
本节学习方法：
(1)数形结合的思想方法；
(2)充分利用圆的几何性质，简化计算；
(3)循序渐近的学习方法.
【重点难点解析】
同学们现在所学习的圆与初中所学习的圆是一样的，也就是说，圆的几何性质仍然成立.所不同的是现在我们把圆放到平面直角坐标系中去研究.这就需要大家在学习本节时，先复习圆的几何意义，几何性质，要复习曲线与方程的概念，从而学习“圆的方程”这一节内容.
例1 求经过点A(-2，-4)且与直线l:x+3y-26=0相切于点B(8，6)的圆的方程.
分析一 设圆的方程为x2+y2+Dx+Ey+F=0则
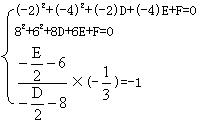
整理得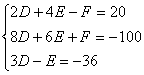
解得D=-11,E=3,F=-30
分析二 设圆心C(a,b)且圆的方程为
(x-a)2+(y-b)2=r2 ∵｜CA｜=｜CB｜,CB⊥l
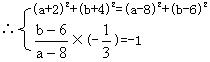
解得a=
,b=-
从而r=
故所求的方程的(x-)2+(y+)2=
分析三 设圆心为C，则CB⊥l，∴CB的方程为y-6=3(x-8),即3x-y+18=0，又AB的垂直平分线的方程为x+y-4=0
联立
∴半径r=
=
∴所求圆的方程为(x-)2+(y+)2=
例2 当m为何值时，直线mx-y-m-1=0与圆x2+y2-4x-2y+1=0相交，相切、相离.
分析一 (判别式法)将y=mx-m-1代入圆的方程化简整理得：
(1+m2)x2-2(m2+
∵△=
当△=0时，得m=0或m=-
时，直线与圆相切.
当△＞0时,得m＞0或m＜-时，直线与圆相交.
当△＜0时，得-＜m＜0时，直线与圆相离.
分析二 (几何法)由已知得圆心坐标为(2，1)半径r=2，圆心(2，1)到直线mx-y-m-1=0的距离d=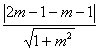
=
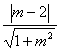
当d=2时，即m=0或m=-时，相切
当d＞2时，即-＜m＜0时，相离
当d＜2时，即m＞0或m＜-时，相交
例3 已知圆C：(x-1)2+(y-2)2=25及直线l:(
(1)证明：不论m取什么实数，直线l与圆C恒相交.
(2)求直线l被圆C截得的弦长最短的长度及此时的直线方程.
分析 若按常规思路只须证圆心O(1，2)到直线l的距离恒小于半径即可.但注意到直线l的方程可变形为x+y-4+m(2x+y-7)=0，则可知直线l恒过定点(3，1)，如果该定点在圆内，问题即可解决，事实上(3-1)2+(1-2)2=5＜25
∴点(3，1)在圆内
这样，不论m为何实数，直线l与圆恒相交.
(2)由(1)的结论可知直线l过定点M(3，1)，且与过此点的圆O的半径垂直时，l被圆所截的弦长｜AB｜最短.
∵｜MO｜=
=
且r=5
∴弦长=2·
=4
此时kl=-
∴-
=-
=2
∴m=-
代入直线l得方程2x-y-5=0
例4 求两圆C1：x2+y2+2x+6y+9＝0和C2:x2+y2-6x+2y+1=0的公切线方程.
分析 要确定公切线的条数，应先判断两圆的位置关系，圆C1的圆心O1(-1,-3),半径r1=1，圆C2的圆心O2(3，-1)，半径r2=3
∵｜O1O2｜=2＞4=r1+r2
∴两圆相离，公切线有四条.
设公切线的交点为M(x0,y0)
(1)外公切线
点M分有向线段O2O1的比为
λ=
=-
=-3
由定比分点公式得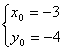
设两圆外公切线方程为y+4=k(x+3)
即kx-y+3k-4=0
由圆心O1（-1，-3）到其距离为1得
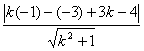=1
即有k=0或k=.
∴两圆的外公切线方程为
y+4=0和4x-3y=0
(2)内公切线
点M（x0,y0）分有向线段O2O1的比为
λ′===-3
由定比分点公式得
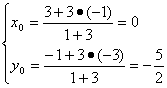
设两圆内公切线方程为y+
=kx
即2kx-2y-5=0
由点O1(-1，-3)到其距离为1得
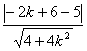=1
解得k=-
∴切线方程为3x+4y+10=0
但由两圆外离，公切线应为4条，说明另一条公切线斜率不存在，则它的方程为x=0.
【难题巧解点拨】
例1 求过两圆x2+y2+4x-3=0与x2+y2-4y-3=0的交点，且圆心在直线2x-y-4=0上的圆的方程.
分析 一般思路是先求出两交点坐标，再结合圆心在直线上，由这三个条件求圆的方程.但计算量较大.可以考虑过两圆交点的圆系方程可设为(x2+y2+4x-3)+λ(x2+y2-4y-3)=0(λ为参数且λ≠-1)整理得圆心坐标为(-
，
)
又∵圆心在直线2x-y-4=0上
代入得：-
--4=0
解得λ=-
代入整理即得所求圆的方程为x2+y2-12x-16y-3=0.
例2 已知定点A(3，0)和B(0，4)，P是△AOB内切圆上的动点(O是原点)，求｜PA｜2+｜PB｜2+｜PO｜2的最大，最小值.
解：本题可直接设P点坐标为(x0,y0),先求出内切圆心方程.再结合P点满足圆的方程代入求其最大.最小值.也可采用参数法求解：
由已知｜AO｜=3，｜BO｜=4，则｜AB｜=5.
设△AOB的内切圆半径为r，则
r=
=1
故△AOB的内切圆方程为(x-1)2+(y-1)2=1
因此可设P点坐标为(1+cosθ,1+sinθ)，有
｜PA｜2+｜PB｜2+｜PO2｜=(2-cosθ)2+(1+sinθ)2+(1+cosθ)2+(3-sinθ)2+(1+cosθ)2+(1+sinθ)2=20-2sinθ
∵-1≤sinθ≤1 ∴18≤20-2sinθ≤22
∴｜PA｜2+｜PB｜2+｜PO｜2的最大值是22，最小值是18.
例3 已知圆O：x2+y2=4，与点A(4，0)，过A点作圆O的割线交圆O于B、C两点，求BC中点M的轨迹方程.
解法一：(定义法)因为BC为圆O的弦，M为弦BC的中点，由垂线定理得OM⊥BC，即OM⊥MA.
∴M点在以OA为直径的圆上.
又OA的中点为(2，0)，｜OA｜=4.
所以点M所在圆心方程为(x-2)2+y2=4.因为ABC是割线，故M点的轨迹是此圆在圆O内部的一段弧.将方程x2+y2=4的两边减去方程(x-2)2+y2=4得x=1,∴M点的轨迹方程为(x-2)2+y2=4(0≤x＜1)
解法二：(直接法)设M点的坐标为(x,y)
(1)当x≠0时，kOM=
,kBC=kMA=
由解法一知DM⊥MA，∴kOM·kBC=-1
即·=-1，化简得x2-4x+y2=0
(2)当x=0时，易知M的坐标为(0，0)，它满足上述方程，∴结合解法一知点M的轨迹方程为x2-4x+y2=0(0≤x＜1＝
解法三：(点差法)设M点的坐标为(x,y)，B、C的坐标分别为(x1,y1),(x2,y2)，则有
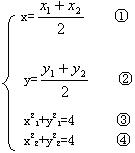
③-④得x21-x22+y21-y22=0
即(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0
∵x1≠x2(否则B与C会重合)
∴x1+x2+(y1+y2)·
=0⑤
又∵A、M、B、C共线，∴kBC=kMA=⑥
将①②、⑥代入⑤得2x+2y· =0
化简得x2+y2-4x=0
同法一得0≤x＜1.
即所求的轨迹方程为x2+y2-4x=0(0≤x＜1)
解法四：(几何法)∵OM⊥MA，∴｜OM｜2+｜MA｜2=｜OA｜2
即x2+y2+(x-4)2+y2=16
即x2+y2-4x=0
同解法一得0≤x＜1
∴所求轨迹方程的x2+y2-4x=0(0≤x＜1)
例4 已知定点A(4，0)和圆x2+y2=4上的动点B，点P分
之比为2∶1，求点P的轨迹方程.
解：(代入法)设动点P(x,y)及圆上点B(x0,y0)
∵λ=
=2
∴
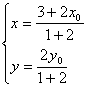于是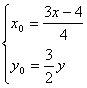
代入圆方程x2+y2=4，得(
)2+
y2=4
∴P点的轨迹方程为(x-)2+y2=
【课本难题解答】
教材第82页，习题7.7
9.答：(1)2x-y-7＝0;
(2)(x-1)2+(y+1)2＝25
10.答：
(0<θ<π)，θ为参数
【典型热点考题】
例1 设圆满足
①截y轴所得的弦长为2；
②被x轴分成两段圆弧，其弧长的比为3∶1，在满足条件①②的所有圆中，求圆心到直线l:x-2y=0的距离最小的方程.
分析 首先求出满足条件①、②的圆的圆心轨迹方程；然后求出圆心到直线x-2y=0的最小距离，最后列出满足圆心坐标与半径r的方程组，确定圆的方程.
解法一：设圆的圆心为P(a,b)，半径为r，则P点到x轴，y轴的距离分别为｜b｜,｜a｜.
由条件②知圆P被x轴截得的劣弧所对的圆心角为90°，从而圆P截x轴所得的弦长为
r.
∴r2=(｜b｜)2=2b2
又圆P截y轴所得的弦长为2，所以有
r=
,∴r2=a2+1
∴圆心P的坐标为(a,b)满足方程2b2-a2=1，
又点P(a,b)到直线x-2y=0的距离为
d=
所以5d2=｜a-2b｜2=a2+4b2-4ab≥(a2+4b2)-2(a2+b2)=2b2-a2=1
当且仅当a=b时上式等号成立，此时5d2=1,从而d取最小值.
由此有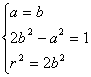
解此方程组得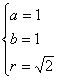
或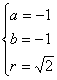
于是，所求圆的方程为
(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2
解法二：同解法一得d=
∴a-2b=±d,即a=2b± d
得a2=4b2±4bd+5d2
将a2=2b2-1代入上式，整理得
2b2±4bd+5d2+1=0
把它看作关于b的二次方程，由于方程有实根，故判别式非负.
即△=8(5d2-1)≥0，得5d2≥1
所以5d2有最小值1，从而d有最小值
.
代入方程2b2±4db+5d2+1=0得b=±1
将b=±1代入r2=2b2,得r2=2.
由a2=2b2-1得a=±1
综上知a=±1，b=±1,r2=2
将d=代入d=得：｜a-2b｜=1知a,b同号.
于是，所求圆的方程是
(x-1)2+(y-1)2=1或(x+1)2+(y+1)2=2
说明：要确定圆心坐标及半径，本题的关键是求出圆心到直线的最小值，解法一利用了基本不等式a2+b2≥2ab求最值.而解法二利用判别式法求最值，这是求最值的两种常用方法.
例2 设有圆心为(ak,0)，半径为rk(k=1,2,3,…)的一系列半圆C1，C2，C3，……，每相邻两个半圆互相外切，并且都和直线l:y=-x+1相切，直线l分别切圆Ck、Ck-1于A、B两点
(1)用rk表示ak;
(2)用rk-1表示rk;
(3)若a1＜0,半圆C1和y轴相切，求r1
(4)在(3)中的半圆C1是这一系列半圆的左起每一个半圆，面积为S1，第k个半圆的面积为Sk(k=1,2,3,…)求S1+S2+…+Sk+……
分析 由题设条件，联想到点到直线的距离公式、数列的有关知识进行解题.
解：(1)由题设得直线l的方程为3x+4y-4=0.
∴rk=d=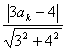
=
∴ak=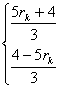
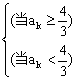
(2)连ACk、BCk-1，过Ck作CkD⊥Ck-1B，则四边形ABDCk为矩形.
∵kAB=kCD，kAB=tanα=-
设直线l分别与x,y轴交于M、N两点.
∴tan∠OMN=tan(180°-α)=-tanα=
sin∠OMN=
又∵sin∠OMN=
=
∴=
rk=
rk-1
(3)∵a1＜0,r1＞0,∴r1=-a1
由点到直线距离公式，得r1=
=
∴r1=2
(4)由(2)得rk=rk-1
r1=2,r2=
,r3=
∴r1,r2,r3,…等比数列，q=
又S1=
πr21=2π
S2= πr22=
π
S3= πr23=
π,……
可知S1，S2，S3……也成等比数例，公比q′=
＜1，
∴S=S1+S2+…=
=
=
π.
例3 当实数x,y满足x2-2x+y2=3时，求｜x｜+｜y｜的最大值与最小值.
分析 圆心方程可化为(x-1)2+y2=4.
令t=｜x｜+｜y｜,∵它的图形是顶点在坐标轴上的正方形，这样问题转化为正方形与圆有公共点时，求t的最大值与最小值.
与圆有公共点的最小正方形是顶点为(1，0)，(0，1)，(-1，0)，(0，-1)故t的最小值为1，与圆有公共点的最大正方形是两边与圆相切的正方形，由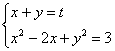
得2x2-2(t+1)x+t2-3=0，由△=0,得t=1+2(1-2 舍去)，即t的最大值为1+2，(t的最大值也可用圆心到直线的距离等于半径去解)
【同步达纲练习】
A级
一、选择题
1.若直线4x-3y-2=0与圆x2+y2-2ax+4y+a2-12=0总有两个不同交点，则a的取值范围是( )
A.-3＜a＜7 B.-6＜a＜4
C.-7＜a＜3 D.-21＜a＜19
2.圆(x-3)2+(y-3)2=9上到直线3x+4y-11=0的距离等于1的点有( )
A.1个 B.2个 C.3个 D.4个
3.使圆(x-2)2+(y+3)2=2上点与点(0，-5)的距离最大的点的坐标是( )
A.(5，1) B.(3，-2)
C.(4，1) D.( +2，-3)
4.若直线x+y=r与圆x2+y2=r(r＞0)相切，则实数r的值等于( )
A.
B.1 C.
D.2
5.直线x-y+4=0被圆x2+y2+4x-4y+6=0截得的弦长等于( )
A.8 B.4 C.2 D.4
二、填空题
6.过点P(2，1)且与圆x2+y2-2x+2y+1=0相切的直线的方程为 .
7.设集合m={(x,y)x2+y2≤25},N={(x,y)｜(x-a)2+y2≤9}，若M∪N=M，则实数a的取值范围是 .
8.已知P(3，0)是圆x2+y2-8x-2y+12=0内一点则过点P的最短弦所在直线方程是 ，过点P的最长弦所在直线方程是 .
三、解答题
9.已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P、Q两点，若OP⊥OQ(O是原点)，求m的值.
10.已知直线l:y=k(x-2)+4与曲线C：y=1+
有两个不同的交点，求实数k的取值范围.
AA级
一、选择题
1.圆(x-3)2+(y+4)2=2关于直线x+y=0的对称圆的标准方程是( )
A.(x+3)2+(y-4)2=2 B.(x-4)2+(y+3)2=2
C.(x+4)2+(y-3)=2 D.(x-3)2+(y-4)2=2
2.点P(5a+1,12a)在圆(x-1)2+y2=1的内部，则实数a的取值范围是( )
A.｜a｜＜1 B.｜a｜＜
C.｜a｜＜
D.｜a｜＜
3.关于x,y的方程Ax2+Bxy+Cy2+Dx+Ey+F=0表示一个圆的充要条件是( )
A.B=0，且A=C≠0 B.B=1且D2+E2-4AF＞0
C.B=0且A=C≠0，D2+E2-4AF≥0 D.B=0且A=C≠0,D2+E2-4AF＞0
4.过点P(-8，-1)，Q(5，12)，R(17，4)三点的圆的圆心坐标是( )
A.(
，5) B.(5，1) C.(0，0) D.(5，-1)
5.若两直线y=x+2k与y=2x+k+1的交点P在圆x2+2=4的内部，则k的范围是( )
A.- ＜k＜-1 B.-
＜k＜1
C.- 
＜k＜1 D.-2＜k＜2
二、填空题
6.圆x2+y2+ax=0(a≠0)的圆心坐标和半径分别是 .
7.若方程a2x2+(2a+3)y2+2ax+a+1=0表示圆，则实数a的值等于 .
8.直线y=3x+1与曲线x2+y2=4相交于A、B两点，则AB的中点坐标是 .
三、解答题
9.求圆心在直线2x-y-3=0上，且过点(5，2)和(3，-2)的圆的方程.
10.光线l从点P(1，-1)射出，经过y轴反射后与圆C：(x-4)2+(y-4)2=1相切，试求直线l所在的直线方程.
【素质优化训练】
一、选择题
1.直线
x+y-2=0截圆x2+y2=4得的劣弧所对的圆心角为(全国高考题)( )
A. 
B.
C.
D.
2.对于满足x2+(y-1)2=1的任意x,y，不等式x+y+d≥0恒成立，则实数d的取值范围是( )
A.［-1，+∞］ B.(-∞，-1)
C.［ +1,+∞］ D.(-∞, +1)
3.若实数x，y满足x2+y2=1,则
的最小值等于( )
A. B. C.
D.2
4.过点P(1，2)的直线l将圆x2+2-4x-5=0分成两个弓形，当大、小两个弓形的面积之差最大时，直线l的方程是( )
A.x=1 B.y=2 C.x-y+1=0 D.x-2y+3=0
5.一辆卡车宽2.7米，要经过一个半径为4.5米的半圆形隧道(双车道，不得违章)，则这辆卡车的平顶车篷篷顶距离地面的高度不得超过( )
A.1.8米 B.3米 C.3.6米 D.4米
二、填空题
6.若实数x,y满足x2+y2-2x+4y=0，则x-2y的最大值是 .
7.若集合A={(x、y)｜y=-｜x｜-2}，B={(x,y)｜(x-a)2+y2=a2}满足A∩B=
，则实数a的取值范围是
.
8.过点M(3，0)作直线l与圆x2+y2=16交于A、B两点，当θ= 时，使△AOB的面积最大，最大值为 (O为原点).
三、解答题
9.令圆x2+y2-4x-6y+12=0外一点P(x,y)向圆引切线，切点为M，有｜PM｜=｜PO｜,求使｜PM｜最小的P点坐标.
10.已知圆C：(x+4)2+y2=4和点A(-2，0)，圆D的圆心在y轴上移动，且恒与圆C外切，设圆D与y轴交于点M、N，求证：∠MAN为定值.
11.已知直角坐标平面内点Q(2，0)，圆C：x2+y2=1，动点M到圆C的切线长与｜MQ｜的比等于常数λ(λ＞0)，求动点M的轨迹方程，并说明轨迹是什么曲线.
12.自点A(-3，3)发出的光线l射到x轴上，被x轴反射，其反射光线m所在直线与圆x2+y2-4x-4y+7=0相切，求光线l与m所在直线方程.
13.AB是圆O的直径，且｜AB｜=2a,M是圆上一动点，作MN⊥AB，垂足为N，在OM上取点P，使｜OP｜=｜MN｜，求点P的轨迹.
参考答案：
【同步达纲练习】
A级
1.B 2.C
3.B 4.D 5.C
6.x=2或3x-4y-2=0 7.-2≤a≤2 8.x+y-3=0，x-y-3=0 9.m=3 10.(
,)
AA级
1.B 2.D
3.D 4.D 5.B
6.(- 
,0), 
7.-1 8.(- 
，
) 9.(x-2)2+(y-1)2=10 10.3x+4y+1=0或4x+3y-1=0
【素质优化训练】
1.C 2.A
3.B 4.D 5.C
6.10 7.-2(+1)＜a＜2(+1) 8.θ=arccot2 或π-arccot2, 8 9.P(
,
) 10.60°
11.M的轨迹方程为(λ2-1)(x2+y2)-4λ2x+(1+4x2)=0，当λ=1时，方程为直线x=
.
当λ≠1时，方程为(x-
)2+y2=
它表示圆，该圆圆心坐标为(,0)半径为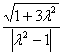
12.l的方程为：3x+4y-3=0或4x+3y+3=0 M的方程为3x-4y-3＝0或4x-3y+3＝0
13.x2+(y±)2=()2轨迹是分别以CO，CD为直径的两个圆.