锥曲线单元试卷(B卷)
班级____ 学号____ 姓名____ 得分____
一、 ?1-2每题 3分, 3-12每题 4分, 共 46分)
1. 
2. 
3. 
A.1,-2 B.-1,2 C.-2,1 D.2,-1
4. 
5. 
6. 已知集合A={(x,y)│x2+y2=1},B ={(x,y)│y2=2(x-a)},若
A∩B= ,则a的取值范围为 [ ]
A.a<-1 B.a>1 C.-1≤a≤1 D.a<-1或a>1
7. 
8. 抛物线y=x2+2Px+q与x轴有两个交点,且交点分别在原点两侧的充要条件是 [ ]
A.P>0,q<0 B.P2-q>0,P>0 C.q<0 D.P2-q>0
9. 方程ㄧxㄧ+ㄧy-1ㄧ=2所表示的图形所围成的面积是 [ ]
A.4 B.8 C.12 D.16
10. 
A.(1,2) B.(2,1) C.(2?) D.(0,0)
11. 已知定圆O内一点P (异于原点O),过P且与圆O相切的圆心轨迹是
[ ]
A.线段 B.椭圆 C.双曲线 D.抛物线
12. 
二、 填空(每道小题 4分 共 20分 )
1. 曲线5x2+9y2+10x-36y-4=0的右焦点坐标是_________________;左准线方程是_____________.
2. 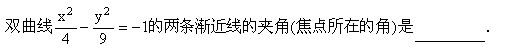
3. 过点P(2,-3)作圆x2+y2=4的切线,切线方程是___________________;它们的夹角等于____________.
4. 
5. 动点到直线x=6的距离是它到点A(1,0)的距离的2倍,那么动点的轨迹方程是_________________________.
三、 解答(第1小题 10分, 第2小题 12分, 共 22分)
1. 求与圆C:x2+y2- 4x+3=0及直线L:x +1= 0都相切的动圆的圆心的轨迹方程.
2. 
四、 证明( 12分 )
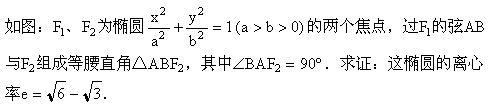
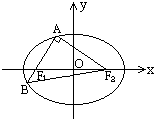
圆锥曲线单元试卷(B卷)答案
一、 单选
1. B
2. D
提示:k=3时,方程无意义.
3. C
4. B
5. A
6. D
7. C
提示:m2
8. C
9. B
提示:
ㄧxㄧ+ㄧy-1ㄧ=2表示的图形是以(0,3)、(2,1)、(0,-1)、(-2,1)
![]()
10. 
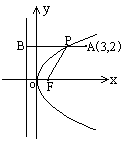
11. B
12. A
提示:如图,旋转后原左焦点成为椭圆的上焦点,新椭圆中心是
(-4,-4),椭圆形状不变.
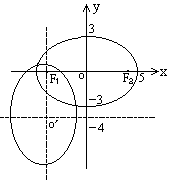
二、 填空
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5. 3x2+4y2+4x-32=0
三、 解答
1. 解:设动圆残腜(x,y),圆半径为R,由定圆C的方程可得圆心(2,0),半径r =1.
(1)若⊙p与⊙C外切,如图1,则有│PC│= R+1,过P点作PA垂直直线
x =-2,垂足是A,
∵⊙p与直线x+1=0相切,根据抛物线定义可知:P点轨迹是以C(2,0)为焦点,直线x=-2为准线的抛物线,P点轨迹方程是y2=8x;
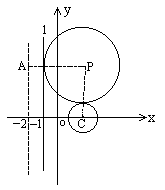
(2)若⊙p与⊙C内切,如图2,则│PC│=R-1,P点到点C(2,0)木嗬胗氲街毕選=0的距离相等,P点的轨迹是以(2,0)为焦点,直线x=0为准线的抛物线,其方程是y2=4(x-1).
综上所述,所求轨迹方程为y2=8x或y2=4(x-1)
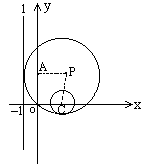
2. 
四、 证明
1.

