|
|
学科:数学 |
| 教学内容:直线的方程 |
【基础知识精讲】
同学们在学习本节知识的过程中,应重视对直线方程的定义的理解,切实掌握直线方程的五种形式,弄清各种形式的适用条件及相互转化.为此应经常性地联想图形位置并实际作图,数形结合、理解、记忆,还应弄清二元一次方程的图象与一次函数的图像间的关系.
直线方程的五种形式及相应的适用范围:
斜截式:y=kx+b,不含垂直于x轴的直线.
点斜式:y-y0=k(x-x0),不含直线x=x0.
两点式:![]() =
=![]() ,不含直线x=x1(y1≠y2)和直线y=y1(x1≠x2).
,不含直线x=x1(y1≠y2)和直线y=y1(x1≠x2).
截距式:![]() +
+![]() =1,不含垂直于坐标轴和过原点的直线.
=1,不含垂直于坐标轴和过原点的直线.
一般式:Ax+By+C=0(A2+B2≠0).适用于平面直角坐标系内的任一直线.
1.本节的主要内容是根据给定条件确定直线的方程,以及讨论直线的有关性质.通常求一条直线的方程就是要确定相应的方程中的参数值,这往往是建立目标量的方程不等式条件组求解,而讨论直线的性质常常是要求出参数的值或范围.
2.求解直线的有关问题应充分运用数形结合的思想方法,灵活选用直线方程的形式.
本节学习了直线方程的五种基本形式,应注意体会从特殊到一般,从一般到特殊的思维方法,善于运用转换与化简的思想处理相关的数学问题.
【重点难点解析】
1.直线斜率的求法
一般地说,求直线斜率有三种方法:
(1)利用定义k=tanα(α≠![]() );
);
(2)利用“两点式”
如果直线过两点A(x1,y1)、B(x2、y2)、(x1≠x2),那么可由公式k=![]() 求直线的斜率;
求直线的斜率;
(3)利用直线的“斜截式”方程.
如果直线l的方程是以一般式给出,即Ax+By+C=0(B≠0),
那么,将l的方程化可为斜截式,即
y=-![]() x-
x-![]()
就可以得到直线l的斜率为-![]() .
.
2.直线方程的求法
一般地,求直线的方程,应结合条件,先考虑选择直线方程的何种形式为宜.最常用的直线的“点斜式”方程和“斜截式”方程中,都含有直线的斜率k,若把k作为参数引入待定,一定要考察直线的斜率是否一定存在,否则容易漏解(即遗漏直线与x轴垂直的情况).
3.直线过定点的问题与二次方程表示直线的问题.
(1)解决直线系恒过定点的问题常常把字母看作参数处理.
(2)若关于x、y的二次方程表示两条直线,这说明方程可分解为两个因式积的形式.常用的方法是判别式法或待定系数法.
例1 若直线ax+by+c=0通过第一、二、三象限,则( )
A.ab>0,bc>0 B.ab>0,bc<
解:化直线方程ax+by+c=0为截距式为![]() +
+![]() =1.直线不过第四象限,所以直线在x轴上截距为负,在y轴上截距为正,即有-
=1.直线不过第四象限,所以直线在x轴上截距为负,在y轴上截距为正,即有-![]() <0且-
<0且-![]() >0
>0![]() ac>0且bc<0,所以ab<0.故选D.
ac>0且bc<0,所以ab<0.故选D.
例2 已知直线过点P(-5,-4),分别求满足下列条件的直线方程:
(1)倾斜角的正弦为![]() .
.
(2)与两坐标轴围成的三角形面积为5.
解:(1)设α是其倾斜角,sinα=![]() ,α∈[0,π),则k=tanα=±
,α∈[0,π),则k=tanα=±![]() .
.
∴ 所求直线方程是 y+4=±![]() (x+5)
(x+5)
即 4x-3y+8=0或4x+3y+32=0
(2)设所求直线方程为![]() +
+![]() =1,因直线过点(-5,-4),所以
=1,因直线过点(-5,-4),所以![]() +
+![]() =1,即4a+5b=-ab.又已知
=1,即4a+5b=-ab.又已知![]() |ab|=5,即|ab|=10.
|ab|=5,即|ab|=10.
解方程组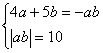 得
得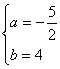 或
或![]() ,故可得所求直线方程为8x-5y+20=0或2x-5y-10=0.
,故可得所求直线方程为8x-5y+20=0或2x-5y-10=0.
例3 求直线ax+by+c=0(a、b不同时为零)的倾斜角.
分析 考虑变形为斜截式,这里需分b=0,b≠0讨论:
(1)当b=0时,方程为x=-![]() .其倾斜角为90°.
.其倾斜角为90°.
(2)当b≠0时,直线即y=-![]() x-
x-![]()
斜率k=-![]()
若![]() ≤0即得倾斜角α=arctan(-
≤0即得倾斜角α=arctan(-![]() )
)
若![]() >0,可得倾斜角α=π-arctan
>0,可得倾斜角α=π-arctan![]() .
.
例4 已知直线过点P(4,-3),且在两坐标轴上的截距的绝对值相等,求直线的方程.
分析 先设出方程的形式,再确定相应的参数.
解法一:由题设知,所求直线的斜率存在且不为0,故可设直线方程为y+3=k(x-4).
令x=0得y=-4k-3,令y=0得x=![]() .
.
由题意得|-4k-3|=|![]() |
|
∴k(4k+3)=±(4k+3)![]() (4k+3)(k+1)(k-1)=0
(4k+3)(k+1)(k-1)=0![]() k=1或k=-1或k=-
k=1或k=-1或k=-![]() .
.
故所求直线方程为x+y-1=0,x-y-7=0,3x+4y=0.
解法二:设直线与两坐标轴的交点分别为(a,0)、(0,b).
(1)当ab≠0时,直线方程为![]() +
+![]() =1.由点P在此直线上,有
=1.由点P在此直线上,有![]() +
+![]() =1 ①又由已知有|a|=|b|
②联立方程①,②可得a=b=1或a=7,b=-7.
=1 ①又由已知有|a|=|b|
②联立方程①,②可得a=b=1或a=7,b=-7.
所以此时直线方程为x+y-1=0,x-y-7=0.
(2)当a=b=0时,直线过原点与点P(4,-3),易知直线方程为3x+4y=0.
综上所述,所求直线方程为x+y-1=0,x-y-7=0,3x+4y=0.
点评:①设斜率参数k时,一定要确定其存在性;使用截距式方程,一定要注意截距非零.②当题设条件不唯一时,通常要对各种情形进行讨论.
【难题巧解点拨】
例1 (1)求证:不论m为何实数,直线(2m-1)x-(m+3)y-(m-11)=0恒过定点,并求出此定点坐标.
(2)二次方程3x2+2xy-y2+7x-5y+k=0表示两条直线.
分析 (1)方法(一):先由m取特值探求,再作一般论证.分别令m=![]() ,m=-3得两直线.
,m=-3得两直线.
-(![]() +3)y-(
+3)y-(![]() -11)=0与(-6-1)x-(-3-11)=0.
-11)=0与(-6-1)x-(-3-11)=0.
易知其交点为(2,3),检验知:
当x=2,y=3时,对m∈R,方程(2m-1)x-(m+3)y-(m-11)=0成立.
故直线过定点(2,3).
方法(二):原直线方程变形为(变更主元)
(x+3y-11)-(2x-y-1)·m=0视为关于m的方程恒成立,于是有
![]()
![]()
![]()
∴ 直线恒过定点(2,3).
(2)方法(一):
①方程变形为3x2+(2y+7)x-(y2+5y-k)=0
Δ=(2y+7)2+12(y2+5y-k)=16y2+88y+(49-12k)
若方程表示两直线,则x=![]() 中,Δ应为y的完全平方式.于是知方程:
中,Δ应为y的完全平方式.于是知方程:
16y2+88y+49-12k=0
的判别式Δ′=882-4×16×(49-12k)=0![]() k=-6.
k=-6.
②当k=-6时,Δ=(4y+11)2.故可知方程3x2+(2y+7)x-(y2+5y-k)=0![]() x=
x=![]()
![]() 3x-y-2=0或x+y+3=0.
3x-y-2=0或x+y+3=0.
方法(二):
由题意可设3x2+2xy-y2+7x-5y+k
=(3x-y)(x+y)+(7x-5y)+k
=(3x-y+A)(x+y+B)
展开右边由待定系数法得:
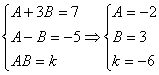
∴ 直线方程为x+y+3=0和3x-y-2=0.
例2 在直角坐标系中,过直线x-y-1=0与直线2x-y-5=0的交点作一直线,使它与两坐标轴围成的面积为24个单位,求这条直线的方程.
分析 根据题意,本题可设所求直线方程为截距式.也可设点斜式求解:
解法一:设所求直线方程为
![]() +
+![]() =1,求得两条已知直线的交点为(4,3)
=1,求得两条已知直线的交点为(4,3)
则有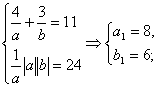
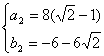 ;
; 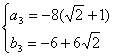
故所求直线有三条:3x+4y-24=0;3(![]() +1)x+4(1-
+1)x+4(1-![]() )y-24=0;
)y-24=0;
3(1-![]() )x+4(1+
)x+4(1+![]() )y-24=0
)y-24=0
解法二:设所求直线斜率为k,由点斜式,所求方程可为y-3=k(x-4).
令x=0,得y=3-4k 令y=0,得x=![]()
∴![]() |(3-4k)
|(3-4k) ![]() |=24;得(4k-3)2=48|k|
|=24;得(4k-3)2=48|k|
若k>0,则(4k-3)2=48k,∴k=![]()
若k<0,则(4k-3)2=-48k,∴k=-![]()
故所求直线方程是:3x+4y-24=0;3(1+![]() )x+4(1-
)x+4(1-![]() )y-24=0;
)y-24=0;
3(1-![]() )x+4(1+
)x+4(1+![]() )y-24=0
)y-24=0
说明:直线在坐标轴上的截距是有向线段的数量而不是长度,故求面积时a,b必须加绝对值.本题也可以用过两直线交点的直线系来解.
例3 过P(3,2)的直线l在两坐标轴上的截距都为正,两交点分别为A,B.
(1)求△AOB的面积的最小值及此时l的方程;
(2)求直线l在两轴上截距之和的最小值(要求用多种方法求解上述问题).
解:(1)△AOB的面积的最小值为12,此时l的方程为2x+3y-12=0;
(2)5+2![]()
【命题趋势分析】
本节考题通常是关于直线方程、倾斜角、斜率、图象的试题,都属于基本要求,以考查基础知识为目的.高考中直线以解答题形式出现的可能性不大,但解答题中关于圆锥曲线的综合题也常考查直线知识,应适当训练一些有关直线知识的小综合题.
【典型热点考题】
例1 过点M(0,1)作直线l,使其夹在两直线l1:x-3y+10=0
l2:2x+y-8=0之间的线段被M平分,求直线l的方程.
分析 所求直线l经过点M(0,1),再找一个条件就可以写出方程,那么只要再求出l上一个点或l的斜率等就行了.
解法一:设l1∩l=P1,l2∩l=P2,l1∩l2=P,作MQ∥l1交于l2于Q点,则Q为PP2的中点,
∴由![]() 得
得![]()
∴P点坐标为(2,4),又MQ的方程为:y-1=![]() (x-0),即x-3y+3=0,
(x-0),即x-3y+3=0,
∴由![]() 得
得![]()
∴Q点坐标为(3,2),因此P2点的坐标为(4,0),
根据两点式方程可得直线l的方程![]() +y=1,即x+4y-4=0.
+y=1,即x+4y-4=0.
解法二:设l的方程为y=kx+1,由![]() 得点P1的坐标为(
得点P1的坐标为(![]() ,
,![]() ),
),
由![]() 得点P2的坐标为(
得点P2的坐标为(![]() ,
,![]() ).
).
∵M(0,1)是P1P2的中点,
∴![]() +
+![]() =0,解之得k=-
=0,解之得k=-![]() .
.
根据直线的点斜式方程可得直线l的方程为:y=-![]() x+1,即:x+4y-4=0.
x+1,即:x+4y-4=0.
解法三:∵P1∈l1,设P1(x1,y1),则x1-3y1+10=0……①
又∵M(0,1)为P1P2的中心,
∴P2的坐标为(-x1,2-y1),由于P2∈l2,所以-2x1+2-y1-8=0,即2x1+y1+6=0……②
由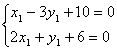
![]()
解之得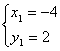 根据直线的两点式方程可得直线l的方程为:
根据直线的两点式方程可得直线l的方程为:![]() =
=![]() ,即x+4y-4=0.
,即x+4y-4=0.
例2 直线l过点M(2,1)且与x轴、y轴的正方向分别交于A、B两点.
(1)求使△AOB的面积最小时的直线l的方程;
(2)求使|MA|·|MB|最小时的直线l的方程;
分析 认真审题,弄清题意,挖掘隐含条件,选择设立合适的直线方程形式是顺利解决综合题的关键.本题考查直线方程、基本不等式、函数最值等知识点.
解:(1)根据意设所求直线方程为![]() +
+![]() =1,显然,a>0,b>0,∵l过点M(2,1) ∴
=1,显然,a>0,b>0,∵l过点M(2,1) ∴![]() +
+![]() =1
=1
解得b=![]() ,由b>0,a>0可知a>2
,由b>0,a>0可知a>2
S△AOB=![]() |a|·|b|=
|a|·|b|=![]() ab=
ab=![]() a·
a·![]() =
=![]()
化简得a2-2as+4s=0 ①
∵a>0,故以上方程有实根.
∴△=4S2-16S≥0,解得S≥4或S≤0(舍去).
∴S=4为面积的最小值,将它代入①式,
得a2-8a+16=0,解得a=4,∴b=![]() =2.
=2.
∴l: ![]() +
+![]() =1.即x+2y-4=0.
=1.即x+2y-4=0.
(2)设所求直线方程为![]() +
+![]() =1,
=1,
由(1)知b=![]() ,且b>0,a>2
,且b>0,a>2
|MA|·|MB|=![]() ·
·![]()
=![]() ·
·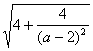
=2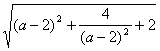 ≥2
≥2![]() =4
=4
当且仅当(a-2)2=![]() 时,|MA|·|MB|取得最小值,由(a-2)4=1可解得a=3或a=1(舍去,∵a>2),当a=3时,b=
时,|MA|·|MB|取得最小值,由(a-2)4=1可解得a=3或a=1(舍去,∵a>2),当a=3时,b=![]() =3,故所求直线方程为:
=3,故所求直线方程为:
![]() +
+![]() =1,即x+y-3=0
=1,即x+y-3=0

【同步达纲练习】
A级
一、选择题
1.下列四个命题中真命题是( )
A.经过定点P0(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示;
B.经过任意两个不同点P1(x1,y1)、P2(x2,y2)的直线都可以用方程(y-y1)(x2-x1)=(x-x1)(y2-y1)表示;
C.不经过原点的直线都可以用方程![]() +
+![]() =1表示;
=1表示;
D.经过定点A(0,b)的直线都可以用方程y=kx+b表示.
2.直线3x+4y-5=0的倾斜角是( )
A.arctan![]() B.arctan(-
B.arctan(-![]() )
)
C.π-arctan![]() D.π+arctan
D.π+arctan![]()
3.若点P(x0,y0)在直线Ax+By+C=0上,则直线方程可表示为( )
A.A(x-x0)+B(y-y0)=0 B.A(x-x0)-B(y-y0)=0
C.B(x-x0)+A(y-y0)=0 D.B(x-x0)-A(y-y0)=0
4.若直线4x-3y-12=0被两坐标轴截得的线段长为![]() ,则c的值为( )
,则c的值为( )
A.1 B. ![]() C.±
C.±![]() D.±1
D.±1
5.过点P(1,1)作直线l,与两坐标轴相交所得三角形面积为10,则直线l有( )
A.1条 B.2条 C.3条 D.4条
二、填空题
6.与直线x-y+![]() =0关于原点成中心对称的直线方程是
.
=0关于原点成中心对称的直线方程是
.
7.将直线y=x+![]() -1绕它上面一点(1,
-1绕它上面一点(1,![]() )沿逆时针方向旋转15°,则所得直线方程为 .
)沿逆时针方向旋转15°,则所得直线方程为 .
8.直线ax-6y-12a=0(a≠0)在x轴上的截距是它在y轴上的截距的3倍,则a等于 .
三、解答题
9.过点A(8,6)引三条直线l1、l2、l3,它们的倾斜角之比为1∶2∶4,若直线l2的方程是y=![]() x,求直线l1、l3的方程.
x,求直线l1、l3的方程.
10.直线l与两坐标轴围成一个面积为18的等腰直角三角形,求直线l的方程.

参考答案:
【同步达纲练习】
A级
1.B 2.C
3.A 4.B 5.D
6.x-y-![]() =0 7.y=
=0 7.y=![]() x 8.-2
x 8.-2
9.解:设直线l2的倾斜角为α,则tanα=![]() ,于是tan
,于是tan![]() =
=![]() =
=![]() =
=![]() ,tan2α=
,tan2α=![]() =
=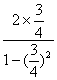 =
=![]() .故所求直线l1的方程为y-6=
.故所求直线l1的方程为y-6=![]() (x-8),即x-3y+10=0,l3的方程为y-6=
(x-8),即x-3y+10=0,l3的方程为y-6=![]() (x-8),即24x-7y-150=0.
(x-8),即24x-7y-150=0.
10.x+y+6=0,x+y-6=0,x-y+6=0,x-y-6=0.
