直线的倾斜角和斜率

	学科：数学
	教学内容：直线的倾斜角和斜率

【基础知识精讲】

课本从此节开始较系统地介绍平面直角坐标系内直线的表示及其性质的运用，建议同学们先复习一次函数的图像与性质，以及正切函数的定义与性质，向量的坐标表示，便于更好地学习本节知识.

本节知识要点：

1.直线的方程和方程的直线的概念.

2.直线的倾斜角的概念，倾斜角范围：0°≤α°＜180°.

3.斜率的概念，k＝tanα.(0°≤α＜180°且α≠90°).

4.过两点的直线的斜率公式k＝.

5.当直线不垂直于x轴时，其方向向量的坐标为(1，k).

本节学习要求

坐标系的建立，使得平面内的点和坐标、曲线和方程等联系起来，为我们运用代数的方法研究几何问题架起了一座“桥梁”，达到了形和数的结合.坐标法是我们研究直线的一种重要方法，也是广泛应用于其它领域的重要数学方法.本节的斜率公式就是通过直线上两点的坐标对直角坐标平面内的直线相对于x轴的倾斜程度的定量刻画.

学习过程中注意体会数形结合的数学思想，逐步学会运用观察、分析、联想、转化等数学方法解决问题.

【重点难点解析】

本小节的重点是直线的倾斜角和斜率概念，过两点的直线的斜率公式，难点是斜率概念的学习和过两点的直线的斜率公式的建立.

1.倾斜角和斜率都是反映直线相对于x轴正方向的倾斜程度的.倾斜角是直接反映这种倾斜程度的，斜率等于倾斜角的正切值.

2.过两点的直线的斜率公式是对斜率的定义式的坐标化.关于斜率公式，应弄清以下几点：(1)斜率公式与两点的顺序无关，即两点的纵坐标和横坐标在公式中的前后次序可以同时颠倒；(2)斜率公式表明，直线对于x轴的倾斜程度，可以通过直线上任意两点的坐标表示，而不需求出直线的倾斜角，因而，使用时较方便；(3)当x₁＝x₂,y₁≠y₂(即直线和x轴垂直)时，直线的倾斜角α等于90°，没有斜率；(4)当α＝0°时，k＝tanα＝0,斜率公式仍适用，只不过此时不必再用公式求得.

例1　经过两点(2，3)和(4，-5)的直线的倾斜角是(　　)

A.arctan4　　  B.arctan(-4)　　　C.π-arctan4　　　D.πtantan4

解：由斜率公式k＝＝＝-4知，直线的倾斜角为钝角，因正切值为-4的相应钝角是π-arctan4，故选C.

例2　设直线的斜率为k，且-<k<，则直线的倾斜角α的取值范围是　　　　　 .

解：由斜率的范围，求倾斜角的范围必须注意倾斜角应在［0，π］内取值.

答：α∈［0，∪(,π

例3　直线l过点A(1，2)、B(m,3)，求l的斜率和倾斜角.

分析　这里m的范围不足，求l的斜率和倾斜角需分类讨论求解.

解：设直线l的斜率为k，倾斜角为α.

(1)当m＝1时，直线l与x轴垂直，斜率k不存在，倾斜角α＝.

(2)当m≠1时，k＝tanα＝＝.

1°当m>1时，α＝arctan

2°当m<1时，α＝π-arctan.

【难题巧解点拨】

例1　(1)如果AC<0且BC<0，那么直线Ax+By+C＝0不通过(　　)

A.第一象限　　　　　　　　  　　B.第二象限

C.第三象限　　　　　　　　　D.第四象限

解：直线方程可变形为y＝-x-

由BC<0知该直线在y轴上的截距->0.

由AC<0,BC<0得ABC²>0,∴AB>0，故该直线的斜率k<0，倾斜角为钝角.作出该直线的示意图知该直线不经过第三象限，选C.

(2)对于直线xcosα+y+1＝0，其倾斜角的取值范围是(　　)

A.［-，］　　　　　　　　　　　B.［,π］

C.［0，］∪［，)　　　　　 D.［0，］∪［，π)

解：斜率为-cosα∈［-1，1］∴选C.

(3)过点A(-1，2)作直线l，使它在x轴、y轴上的截距相等，则这样的直线(　　)

A.只有1条　　　　　　　　　　　B.只有2条

C.只有3条　　　　　　　　　　　D.共有4条

解：过原点和斜率为-1的两条直线满足题意，选B.

例2　已知3x+5y+14＝0，其中x∈［-3，2］，求：｜｜的最小值.

解：由已知得线段：3x+5y+14＝0,x∈［-3，2］的两个端点A(-3，-1)，B(2，4)，而｜｜可以看作线段AB上的点与点(-1，-2)连线斜率的绝对值，记P(-1，-2)，则k_PA＝-，k_PB＝-，当3x+5y+14＝0,x∈［-3，2］时，k＝,x∈［-,- ］,∴｜k｜_min＝.

即｜｜的最小值是.

【命题趋势分析】

本节考点为直线倾斜角的概念、范围，过两点的直线的斜率公式及简单应用，考题通常是与直线方程、三角函数的性质、公式等相联系的综合题.

预测考题：

1.如果AC<0且BC<0，那么直线Ax+By+C＝0，不通过(　　)

A.第一象限　　　　　　　  　B.第二象限

C.第三象限　　　　　　　　　D.第四象限

2.已知有向线段的起点A和终点B的坐标分别为A(-1，1)和B(2，2)，过点(0，-1)的直线l与有向线段不相交，则直线l的斜率的取值范围是　　　　　　 .

【典型热点考题】

例1　已知一条直线的倾角是arcsin，且它与两坐标轴围成的三角形的面积为6，求此直线方程.

解：因为所求直线的倾角是arcsin是锐角.且这个角的正切为，所以直线的斜率为.

设所求直线的方程为y＝x+b

直线与坐标轴的交点分别是(-b,0)和(0,b)

由题意得｜b｜·｜-b｜＝6

∴｜b²｜＝9　即b²＝9

∴b＝±3

∴所求直线的方程为y＝x±3

即3x-4y+12＝0和3x-4y-12＝0

例2　已知直线l经过点P(2，1)，且它的倾斜角等于已知直线l′：3x-4y-17＝0的倾斜角的，求l的方程.

分析　求l的方程可借助求一次函数解析式的方法，用待定系数法由已知倾斜角的关系求斜率，用已知线上的点求纵截距.

解：设直线l′的倾角为α，则l的倾角为.

∴tanα＝>0,0<x<，

∴cosα＝＝

∴tan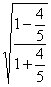＝＝＝故所求直线方程为x-3y+1＝0

说明：求半角的正切值，根据所在象限确定符号，只取正值得一解.如果求出的tanα＝-3或tanα＝有二解，从而忽视了对α所在象限的讨论，不会舍去tanα＝-3而多解.

【同步达纲练习】

A级

一、选择题

1.经过两点M(6，8)、N(9，4)的直线的倾斜角为(　　)

A.arctan　　　　　　　　  　　B.arccot

C.arctan(-)　　　　　　　　　 D.π-arctan

2.若图中的直线l₁、l₂、l₃的斜率分别为k₁、k₂、k₃，则有(　　)

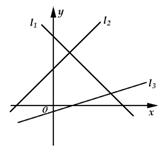
A.k₁<k₂<k₃　　 　 B.k₃<k₁<k₂  C.k₃<k₂<k₁　　　　　 D.k₁<k₃<k₂

3.若三点A(3，1)，B(-2，b)，C(8，11)在同一直线上，则实数b等于(　　)

A.2　　　　　　　B.3　　　　　　　C.9　　　　　　　 D.-9

4.直线ax+by＝ab(a>0,b<0)的倾斜角是(　　)

A.arctan(-)　　　　　　　　　　 B.arctan

C.π-arctan　　　　　　　　　 　 D. +arctan

5.若α是直线的倾斜角，则sin(-α)的取值范围是(　　)

A.［-1，］　　　　　　　　　　　B.(-1，)

C.(- , )　　　　　　　　　　　　D.［-,)

二、填空题

6.若ab<0，则方程ax+by＝1表示的直线的倾斜角的取值范围是　　　　　　 .

7.已知点P(3，-1)，MP连线的倾斜角为arctan，且｜MP｜＝3,则点M的坐标为　　　 .

8.已知直线的斜率的绝对值为，则此直线的倾斜角为　　　　　  .

三、解答题

9.已知A(-3，2)、B(a,3)，求直线AB的斜率与倾斜角.

AA级

一、选择题

1.下列说法中正确的是(　　)

A.一条直线和x轴的正方向所成的正角，叫做这条直线的倾斜角.

B.直线的倾斜角α的取值范围是第一或第二象限角.

C.和x轴平行的直线，它的倾斜角为180°.

D.每一条直线都存在倾斜角，但并非每一条直线都存在斜率.

2.下列多组点中，三点共线的是(　　)

A.(1，4)，(-1，2)，(3，5)　　　　　 B.(-2,-5),(7,6),(-5,3)

C.(1,0),(0,-),(7，2)　　　　　　　D.(0，0)，(2，4)，(-1，3)

3.已知直线l₁的方程是ax-y+b＝0,l₂的方程是bx-y-a＝0(ab≠0,a≠b)，则下列各示意图形中，正确的是(　　)

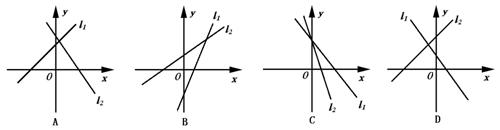
4.设点A(2，-3)，B(-3，-2)，直线l过点P(1，1)且与线段AB相交，则l的斜率k的取值范围是(　　)

A.k≥或k≤-4　　　　　　　　　　 B.k≥或k≤-

C.-4≤k≤　　　　　　　　　　　　 D.- ≤k≤4

5.过原点引直线l，使l与连接A(1，1)和B(1，-1)两点的线段相交，则直线l倾斜角的取值范围是　　　　　　 .

6.已知A(-sinθ,cos²θ),B(0,1)是相异两点，则直线AB的倾斜角的取值范围是　　　　　　 .

7.要使三点A(2，cos²θ),B(sin²θ,- ),C(-4,-4)共线，则角θ的值为　　　　　  .

8.已知直线(2a²-7a+3)x+(a²-9)y+3a²＝0的倾斜角为，则实数a＝　　　　　  .

【素质优化训练】

1.已知点M(rcosα,rsinα),N(rcosβ,rsinβ),(-<  <)，则直线MN的倾斜角为(　　)

A. 　　　　　　　　　 B.

C. 　　　　　　　　　 D.α+β-π

2.若点P₁(2，3)，P₂(3，a)，P₃(4，b)共线，则(　　)

A.a＝4,b＝5　　　　　　　　　　 B.b-a＝1

C.2a-b＝3　　　　　　　　　　　 D.a-2b＝3

3.在直角坐标系中，△ABC的三个顶点是A(0，3)、B(3，3)、C(2，0)，若直线x＝a将△ABC分成面积相等的两部分，则实数a的值为(　　)

A.　　  　　 B.1+　　  　　　C.1+　　 　 　　D.2-

4.点(a+b,c)、(b+c,a)和(c+a,b)的位置关系是(　　)

A.同在一条直线上　　　　　　　　　　　　B.三点间的距离两两相等

C.三点连线组成一个直角三角形　　　　　　D.三点连线组成一个等边三角形

5.设α是直线l的倾斜角，且满足：sinα+cosα＝，则直线l的斜率为(　　)

A. 　　　　　 B.-或-　　　　 C. 　　　　　 D.-

6.过点P(-1，2)的直线l与x轴和y轴分别交于A、B两点，若P分所成的比＝，求直线l的斜率和倾斜角.

补充题：

1.如果AC<0且BC<0，那么直线Ax+By+C＝0，不通过(　　)

A.第一象限　　　　 　　　　 B.第二象限

C.第三象限　　　　　　　　　D.第四象限

2.已知有向线段的起点A和终点B的坐标分别为A(-1，1)和B(2，2)，过点(0，-1)的直线l与有向线段不相交，则直线l的斜率的取值范围是　　　　　　 .

参考答案：

【同步达纲练习】

A级

1.D　2.D  3.D　4.A　5.A  6.(0，)　7.( ，)或(，-)　8.60°或　9.解：a=-3时，斜率不存在，倾斜角为;a≠-3时，斜率k==.当a＞-3时，倾斜角为arctan ;当a＜-3时，倾斜角为π+arctan

AA级

1.D　2.C  3.D　4.A　5.［0, ］∪［π，π］　6.(0, )∪［，π］　7.θ=,k∈Z　8.-

【素质优化训练】

1.A　2.C  3.A　4.A　5.D

6.解：设A(x,0),B(0,y)，则

　 ∴

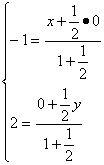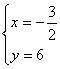
即得A(-，0)，B(0，6)

∴k_AB=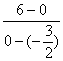=4,倾斜角α=arctan4.

补充题：

1.C　2.(-2，)