直线和圆的方程达标检测(A级)

	学科：数学
	教学内容：；直线和圆的方程达标检测(A级)

【同步达纲练习】

(A级　达纲级)

一、选择题(3′×8)

1.直线ax+by+c＝0通过第一、二、三象限，则(　　)

A.ab>0,bc<0　　　　　　　 　　　B.a＝0,bc<0

C.ac>0,bc<0　　　　　　　　　　 D.c=0,ab>0

2.三条直线2x+3y＝1,3x+2y＝1,ax-y-1＝0交于一点，则a的取值是(　　)

A.a＝3　　　　　B.a＝6　　　　　C.a＝-6　　 D.a＝

3.过点B(2，3)且在两坐标轴上有相等截距的直线方程只能是(　　)

A.x+y-5＝0　　　　　　　　　　　B.x+y+5＝0

C.x+y-5＝0或x+y+5＝0　　　　　 D.x+y-5＝0或2x-2y＝0

4.直线x+2y-2＝0的倾斜角为(　　)

A.arctan(-)　　　　　　　　　 B.π-arctan

C.π-arctan2　　　　　　　　　　D.π+arctan

5.“A＝3”“是直线Ax-2y-1＝0与直线6x-4y+c＝0平行”的(　　)条件.

A.充要条件　　　　　　　　　　　B.充分不必要条件

C.必要不充分条件　　　　　　　　D.既不必要也不充分

6.无论a,b为何值，直线(2a+b)x+(a+b)y+a-b＝0都通过定点(　　)

A.(3,-2)　　　　　　　　　　　　B.(-2，3)

C.(-2，-3)　　　　　　　　　　　D.(-3，-2)

7.如果点(4,a)到直线4x-3y-1＝0的距离不大于3，那么a的取值范围是(　　)

A.(0,10)　　　　B.　　　C.［0，10］　　　　 D.(-∞，0］∪［10，+∞)

8.已知三条不同直线l₁:A₁x+B₁y+C₁＝0,l₂:A₂x+B₂y+C₂＝0,l₃:A₃x+B₃y+C₃＝0(其中A₃＝A₁+A₂，B₃＝B₁+B₂，C₃＝C₁+C₂)，那么l₁,l₂,l₃的位置关系是(　　)

A.两两平行　　　　　　　　　　　B.两两相交且过同一点

C.两两相交但不过同一点　　　　　D.两两平行或交于同一点

二、填空题(4′×2)

1.直线(3a+2)x+(1-4a)y+8＝0与(5a-2)x+(a+4)y-7＝0互相垂直，则a的值为　　　　　　 .

2.平面上一个动点到两个坐标轴的距离相等，这个动点的轨迹方程是　　　　　　 .

三、解答题

1.已知A(1，2)，B(5，4)和直线x-2y-2＝0上一动点P，且点P使｜PA｜+｜PB｜最小，求点P的坐标.(12′)

2.已知△ABC三边所在直线方程是AB：4x-3y+10＝0;BC:y-2＝0;CA:3x-4y-5＝0.求：(15′)

①∠B的大小；

②∠BAC内角平分线方程；

③AB边上的高所在直线方程.

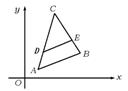
3.如图，△ABC中，DE∥AB，A(1，1)，C(4，5)且S_△CDE＝S_{四边形ABED}，求D点坐标.(12′)

4.P为直线l:Ax+By+c＝0上一动点，M(a,b)为一定点，点Q在直线MP上，且MQ：QP＝λ，求Q点轨迹(λ≠-1，λ≠0).(15′)

5.北京华掀公司计划在今年内同时出售“夜莺牌多功能”电子琴和“OK智能型”洗衣机，由于两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量，以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于两种产品有关数据如下表：

资金　　　　　　　 单位产品所需资金　　　　　　 月资金供应量 　　　　　　　 　　　　　　 (百元)

成本　　　　　　 30　　　　　　　 20　　　　　　　　　 300

劳动力(工资)　　　5　　　　　　　 10　　　　　　　　　 110

单位利润　　　　  6　　　　　　　  8

试问：怎样确定两种货的供应量，才能使总利润最大，最大利润是多少?(14′)

参考答案:

【同步达纲练习】

A级

一、1.C　2.B  3.D　4.B　5.C  6.B　7.C　8.D

二、1.a＝0或a＝1　2.y＝±x

三、1.P(0，1)　2.∠B＝π-arctan；∠BAC内角平分线方程是7x-7y+5＝0;AB边上的高所在直线方程是3x+4y-21＝0　3.D(4-,5-2).　4.Q点的轨迹是与直线l平行的一直线.　5.当供应量为电子琴4架，洗衣机9台时该可获得最大利润，最大利润为96(百元).