试卷类型：A

高中调研高二数学测试题

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页，共150分，考试时间120分钟．

第 Ⅰ 卷 (选择题，共60分)

注意事项：

1．请考生将自己的姓名、学号、班级填写在第Ⅱ卷密封线内．

2．每小题选出答案后在第Ⅱ卷前的答题栏内用铅笔把对应题目的答案代号涂黑，如需改动，必须用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．

一．选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1.　若直线过点(，－3)，且倾斜角为30°，则直线的方程为
　　A．　　　 B．　　　 C．　　　　 D．

2.　直线x－2y＋2＝0与直线3x－y＋7＝0的夹角等于
　　A．　　　　　　　　　　B．　　　　　　　　　　　 C．　　　　　　　　　　 D．arctan 7

3.　不等式ax²＋bx＋2＞0的解集是，则a－b等于
　　A．－4　　　　　　　　　　　B．14　　　　　　　　　　　　C．－10　　　　　　　　　　 D．10

4.　抛物线＝－2y²的准线方程是
　　A．　　　　　　　 B．　　　　　　　 C．　　　　　　　　　D．

5.　已知a、b、c∈R，下列命题正确的是
　　A．a＞b Þ ac²＞bc²　　　　　　　　　　　　　　　　　 B．
　　C．　　　　　　　　　　　　　　　 D．

6.　过点P(2，1)且被圆C：x²＋y²－2x＋4y＝0 截得弦最大的直线l的方程是
　　A．3x－y－5＝0　　　　 B．3x＋y－7＝0　　　　 C．x＋3y－5＝0　　　　 D．x－3y＋5＝0

7.　不等式1＜｜x－2｜≤7的解集是
　　A．[3，9]　　　　　　　　　　　　　　　　　　　　　　　　　 B．[－5，9]
　　C．[－5，1]∪[3，9]　　　　　　　　　　　　　　　　　 D．[－5，1)∪(3，9]

8.　设0＜a＜，下列不等式成立的
　　A．　　　　　　　　B．
　　C．　　　　　　　　 D．

9.　双曲线的焦点在y轴上，则m的取值范围是
　　A．(－2，2)　　　　　　　 B．(1，2)　　　　　　　　　C．(－2，－1)　　　　　 D．(－1，2)

10. 函数的最小值是
　　A．2　　　　　　　　　　　　　B．0　　　　　　　　　　　　　C．1　　　　　　　　　　　　　D．3

11. 已知椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点．一水平放置的椭圆形台球盘，点A，B是它的焦点，长轴长为2a，焦距为2c．当静放在点A的小球（小球的半径不计），从点A沿直线出发，经椭圆壁反弹后再回到点A时，小球经过的路程是
　　A．4a　　　　　　　　　　　　B．2(a－b)　　　　　　　　C．2(a＋c)　　　　　　　　 D．以上答案都可能

12. 若对于任意的实数，不等式｜x＋1｜≥kx恒成立，则实数k的取值范围是
　　A．(－∞，0]　　　　　　 B．[－1，1]　　　　　　　 C．[0，1]　　　　　　　　　D．[1，＋∞)

第Ⅰ卷答题栏

[ A ]

[ B ]

[ C ]

[ D ]

高中调研测试题

高二数学

第 Ⅱ 卷 (非选择题，共90分)

注意事项：

第Ⅱ卷共6页，用钢笔或圆珠笔直接答在试题卷中，答卷前将密封线内的项目填写清楚．

题号	一	二	三						总　分
题号	一	二	17	18	19	20	21	22	总　分
得分

得分	评卷人

二．填空题：本大题共4小题，每小题4分，共16分．将正确答案填在题中横线上．

13. 过点(1，2)和直线x－y＝0平行的直线是　　　　　　　　　．

14. 点(3，1)和(－4，6)在直线3x－2y＋a＝0的两侧，则a满足　　　　　　．

15. 不等式的解集是　　　　　　　　　　　　　．

16. 若实数x，y满足x²＋(y－1)²＝2，且x＋y＋d＝0，则实数d的取值范围是　　　　　　．

三．解答题：本大题共6小题，满分74分．

得分	评卷人

17.　 (本大题满分12分) 已知a、b为正数，n∈N*，证明不等式：
　　　　　　≤．

得分	评卷人

18.　 (本大题满分12分) 已知P(2，0)，Q(8，0)，点M到点P的距离是它到点Q距离的，求点M的轨迹方程，并求轨迹上的点到直线l：8x－y－1＝0的最小距离．

19.　 (本大题满分12分) 自点A(－3，3)发出的光线l射到x轴上被x轴反射，其反射光线所在的直线与圆x²＋y²－4x－4y＋7＝0相切，求反射光线所在直线的方程．

得分	评卷人

20.　 (本大题满分12分) 解关于的不等式 (x∈R)．

得分	评卷人

21.　 (本大题满分12分) 某厂生产甲、乙两种产品，甲种产品每单位需A种原料8克，B种原料24克，每单位利润60元；乙种产品每单位需A种原料和B种原料各16克，每单位利润80元．现有A种原料2400克，B种原料2880克，问甲、乙两产品各生产多少单位，工厂可获得最大利润(原料不再外购，产品可完全售出)．

得分	评卷人

22.　 (本大题满分14分) 如图，已知椭圆(2≤m≤5)，过其左焦点且斜率为1的直线与椭圆及其准线交于A、B、C、D，设f (m)＝AB－CD ．
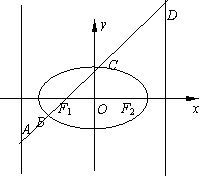　　(1)求f (m)的解析式；
　　(2)求f (m)的最大、最小值．

得分	评卷人

高中调研测试题

高二数学参考答案及评分标准

一．选择题：ABCDC　 ADACC　 AC

二．填空题：

13．x－y＋1＝0　14．(－7，24)　 15．{x｜－＜x＜1或x＞}　　16．[－3，1]

三．解答题

17．证：∵a、b为正数，∴不等式等价于．
　　　　　　　4分
　　当a≥b时，a－b≥0，aⁿ≥bⁿ，即bⁿ－aⁿ≤0，∴(a－b)( bⁿ－aⁿ)≤0，　　　　　　6分
　　当a＜b时，a－b＜0，aⁿ＜bⁿ，即bⁿ－aⁿ＞0，∴(a－b)( bⁿ－aⁿ)＜0，　　　　　　　　　　 8分
　　因此≤0 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　即
　　∴原不等式成立．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

18．解：设M(x，y)，则，
　　由题意得，MP＝MQ，∴　　　　　　　　　　　　　　 4分
　　化简并整理得：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分
　　所求轨迹是以(，0)为圆心，为半径的圆
　　圆心到直线l的距离为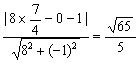　　　　　　　　　　　　　　　　　　　　　　　　　　　　 10分
　　∴圆上的点到直线l的最小距离为．　　　　　　　　　　　　　　　　　　　　　　　　 12分

19．解：点A(－3，3)关于x轴的对称点为B(－3，－3)
　　反射线所在直线过点B，设其方程为y＋3＝k(x＋3)，即kx－y＋3k－3＝0　　　　4分
　　圆x²＋y²－4x－4y＋7＝0的方程可化为　(x－2)²＋(y－2)²＝1
　　∵反射线所在直线与圆相切，∴　　　　　　　　　　　　　　　　　　6分
　　解得　k＝或k＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　10分
　　∴所求直线方程为：3x－4y－3＝0或4x－3y＋3＝0．　　　　　　　　　　　　　　　　　　　　　　 12分

20．解：由，得　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 2分
　　此不等式与同解　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　3分
　　若a＜0，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　6分
　　若a＝0，则x＜0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　8分
　　若a＞0，则x＜0或x＞　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 11分
　　综上，a＞0时，原不等式的解集是(－∞，0)∪(，＋∞)；
　　　　　a＝0时，原不等式的解集是((－∞，0)；
　　　　　a＜0时，原不等式的解集是(，0)　　　　　　　　　　　　　　　　　　　　　　　　　　　12分

21．解：设生产甲、乙两种产品分别为x单位、y单位，所获利润为z元，
　　则z＝60x＋80y　　　　　　　　　　　　 2分
　　依题意，有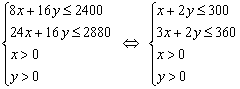 4分
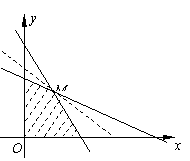
　　作出不等式组表示的平面区域如图　　　　 8分
　　由得M(30，135)
　　将直线60x＋80＝z平移过点M，即x＝30，y＝135时，z取到最大值　　　　　　　　10分
　　∴甲、乙两种产品分别生产30单位和135单位时，工厂可获得最大利润．　　　12分

22．解：(1)设椭圆的焦距为c，则c²＝m－(m－1)＝1，则
　 F₁(－1，0)，F₂(1，0)，椭圆的准线为x＝±m，直线的方程为y＝x＋1
　　易知A(－m，－m＋1)，B(m，m－1)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　4分
　　由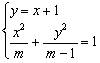消去y并整理得：(2m－1)x²＋2mx＋2m－m²＝0　　　　　　　　　 6分
　　△＝8m(m－1)²，∵ m∈[2，5]，∴△＞0恒成立
　　此时，又直线的斜率k＝1
　　∴　　　　　8分
　　又x_A＝－m，x_D＝m，∴x_A＋x_D＝0
　　故 m∈[2，5]　　　　　　　　　　　　　　　　　　　　　　　　　　 10分

(2)解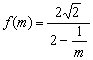：，又m∈[2，5]，易知
　　∴，故　　 14分