[科目] 数学
[年级]
[考试类型] 同步
[关键词] 函数/单调性/奇偶性
[文件] sxtbgd8.doc
[标题] 函数的单调性与奇偶性(２)
[内容]
函数的单调性与奇偶性(２)
一、选择题
1．函数f（x）=
在第一象限为减函数，则m的取值范围是
（ ）
（A）-2＜m＜1（B）m∈R（C）m＜-2或m＞1（D）φ
1． 设f（x）=（x+2）3，则函数y=f（x-2）
（A） 是偶函数（B）是减函数（C）是奇函数（D）图象关于（1，0）对称
3．下列函数中既是奇函数又是偶函数的是 （ ）
（A） f（x）=1，x∈R（B）f（x）=x2，x∈〔-3，3〕
（B） f（x）=0，x∈R（D）f（x）=x+
，x≠0
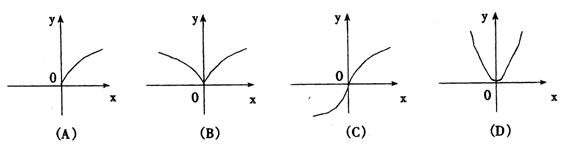
4．函数y=
的图象是 （ ）
5．设函数f（x）=ax3+bx+10，f（1）=5，则f（-1）等于 （ ）
（A） 5（B）-5（C）10（D）15
6．下列命题中正确的是 （ ）
（A） y=2x2+x+1是R上的偶函数（B）y=x3是区间〔a，b〕上的奇函数
（B） y=x是R上的偶函数（D）
是偶函数
7．若a=1.
，
，c=1，则a、b、c的大小关系是 （
）
（A）c＞b＞a（B）a＜c＜b（C）a＞c＞b（D）b＞a＞c
8．下列函数中既是奇函数，又在定义域上单调递减的是 （ ）
（A） y=-x3（B）y=-x3（C）
（D）
9．已知函数y=f（x）是偶函数，且x＞0时，f（x）单调递减，若x2＞0，x2＜0，且x1＜x2，则 （ ）
（A） f（x1）＜f(x2)（B）f(-x2)＞f（x1）
（B） f（-x1）＞f（-x2）（D）f（-x1）＜f（-x2）
10．奇函数y=f（x）（x∈R）的图象上必有点 （ ）
（A）（a，f（-a））（B）（-a，f（a））
（C）（-a，-f（a）） （D）（a，f（a-1））
11．函数y=（x+1）-2的定义域和值域分别是 （ ）
（A） x∈（-1，+∞），y∈〔0，+∞〕
（B） x∈〔-1，+∞〕，y∈〔0，+∞〕
（C） x∈（-∞，-1）∪（-1，+∞），y∈（0，+∞）
（D） x∈（-∞，-1）∪（-1，+∞），y∈〔0，+∞〕
12．函数y=
的定义域是 （ ）
（A）（-∞，0）（B）
（C）
（D）（0，+∞）
13．下列命题中错误的是 （ ）
（A） 若k≠0，则f（x）=
是减函数
（B） 二次函数y=ax2+bx+c，当a＜0时，在
上是增函数，在
上是减函数
（C） 函数y=
在其定义域上是减函数
（D） 函数y=x4在上单调递减，在上单调递增
14． 已知f（x）=ax2+bx+c（a≠0）是偶函数，那么g（x）=ax3+bx2+cx是 （ ）（A）偶函数（B）奇函数（C）非奇非偶函数（D）是奇函数又是偶函数
15． 已知f（x）是奇函数，且当x∈（0，+∞）时，f（x）=x2-2，那么当x∈（-∞，0）时，f（x）等于
（A） x2-2（B）-x2-2（C）2-x2（D）x2+2
一、填空题
16．
已知函数y=x-a在区间
上是增函数，那么a的取值范围是__________.
17． 一次函数y=f(x)满足f(1)=1,f(2)=3,则f(5)=___________.
18．
已知函数f(x)=ax2+bx+c(a≠0)，则
19． 若函数f（x）为偶函数，且当-2≤x≤0时，f（x）=x+1，那么当0＜x≤2时，f（x）=_________.
20.函数y=
的递增区间为__________.
二、解答题
21．
知f（x）=x+，（x≠0），判断f（x）的奇偶性，并按单调性定义证明，f（x）在（0，1）上是减函数，在（1，+∞）上是增函数.
22． 若x，y满足x2+y2=2x，求x2-y2的最大值和最小值.
23．
已知f(x)=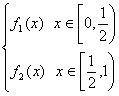
,其中f1(x)=-2(x-
)2+1,f2(x)=-2x+2,
(i) 画出y=f(x)的图象
(ii)
若x0∈
，x1=f（x0），f（x1）=x0，求x0
24． 设f（x）是定义在实数集R上的函数，且对任何x1，x2∈R满足f（x1+x2）=f（x1）+f（x2），求证f（0）=0，且f（x）是奇函数.
25．
设f（x）=
（i）
判断函数f（x）在上的单调性，并按单调性定义证明.
（ii） 求f（x）的值域.
答案
一、选择题
1.A 2.C 3.C 4.B 5.D 6.C 7.B 8.A 9.C 10.C 11.C 12.D 13.A 14.B 15.C
二、填空题
16．α≤2 17.9 18.
19.-x+1 20.
三、解答题
21．f（x）为奇函数，证明略
22．提示：由y2=2x-x2≥0得0≤x≤2，x2-y2=x2-（2x-x2）=2x2-2x，最小值为-，最大值为4.
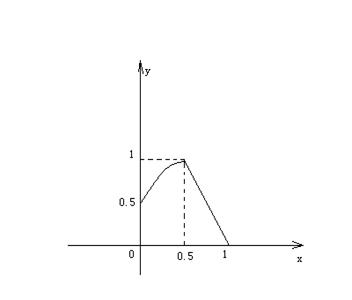
23．（i）如右图.
（ii）由x0∈，得f1（x0）=-2（x0-）2+1，
∴x1=1-2（x0-）2，x1∈〔，1〕
f（x1）=f2（x1）=2-2〔1-2（x0-）2〕=x0
得
x0=1，x0=
∵x0∈∴x0=
24．提示：令x1=x2=0，代入得f（x）=0，令x1=x，x2=-x，代入可证
25．f（x）在上为减函数，单调性证明略，值域为y∈
，由
得
即可求出.