高二数学期中测试题4

高中学生学科素质训练

　

高二数学期中测试题4

（120分钟，满分150分）

题号	一	二	三						总分
			17	18	19	20	21	22
得分

一．选择题（本大题共12小题，每小题5分，共60分）

1． 若直线x =1的倾斜角为α，则α=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　　）

　A． 0°　　　　　　　　　　　 B．45°　　　　　　　　　C． 90°　　　　　　　　　 D．不存在

2．已知直线的斜率等于－2，则直线的倾斜角等于　　　　　　　　　　　　　　　　　　　　　　　　 （ 　　）

A． 　　　　　　　　　　　　　　　　　　　 B． 　 

C． 　　　　　　　　　　　　　　　 D．

3．已知直线l₁和l₂夹角的平分线为y = x，如果l₁的方程是a x +b y +c=0 (ab>0)，那么l₂的方程是　　　　　　　　　 （　　　）

A．b x +a y +c=0　　　　　　　　　　　　　　　　　　 B．a x -b y +c=0

C．b x +a y -c=0　　　　　　　　　　　　　　　　　　　D．b x -a y +c=0

4．使不等式x+1＜2x成立的充分不必要条件是　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

A．－＜x＜1　　　　　B．x＞－　　　　　　C．x＞1　　　　　　　　　　 D．x＞3

5．已知f(x)=,a、b为两个不相等的正实数，则下列不等式正确的是　　　 （　　　）

A．f()＞f()＞f()　　　　　　 　　　 B．f()＞f()＞f()

C．f()＞f()＞f() 　　　　　D．f()＞f()＞f()

6．若a>b>1，，，，则　　　　　　　　　　 （　　　）

A．R<P<Q　　　　　　　　 B．P<Q<R　　　　　　　C．Q<P<R　　　　　　　　 D．Ｐ<R<Q

7．已知a+b=1，则a⁴+b⁴的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

A．2　　　　　　　　　　　　 B．8　　　　　　　　　　　 C． 　　　　　　　　　　　D．

8．一批长200cm的不锈钢条，需要将其截成长18cm和38cm的两种毛坯，则不锈钢条的最大利用率是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　　　　　　　　　　　　　）

　　　 A．99%　　　　　　　　　　B．100%　　　　　　　　 C．85%　　　　　　　　　　　 D．95%

9．

图中阴影部分可用不等式表示为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

　　　 A．　　　　　　　　B．

　　　 C．　　　　　　　D．

10．若am<0, bm<0, 则直线a x +b y +m=0不经过　　　　　　　　　　　　　　　　　　　　　　　　　（　　　）

A．第一象限　　　　　　B．第二象限　　　　　 C．第三象限　　　　　　 D．第四象限

11．已知A(2，－1)，B(5，3)，直线l：2x－y +1=0与AB所在直线相交于点P，则点P分有向线段AB所成的比的值为　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．=－ 　　　　　　B．=－ 　　　　　C．=－　　　　　　　 D．=－

12．甲、乙两工厂2002年元月份产值相同，甲厂的产值逐月增加，且每月增加的产值相等，乙厂的产值也逐月增加，且每月增长的百分率相等，已知2003年元月份两厂的产值相等，则2002年7月份产值高的工厂是　　　　　　　　　（　　　）

A．甲厂　　　　　　　　　 B．乙厂　　　　　　　　　C．产值一样　　　　　　 D．无法确定

二．填空题（本大题共4小题，每小题4分，共16分）

13．过点A（1，-4）且与直线2 x +3 y +5=0平行的直线方程是　　　　　　　　　 ．

14．已知奇函数f(x)在(0，+∞)内单调递增，且f(2)=0，则不等式(x－1)·f(x)＜0的解集

是　　　　　　　　　　　　　　　　　　 ．

15．已知O（0，0）和A（6，3）两点，若点P在直线OA上，且，又P是线段OB的中点，则点B的坐标是　　　　　　　　　　  ．

16．不等式 的解集是　　　　　　　　　　　　　　　　  ．

三．解答题（本大题共6小题，共74分）

17．已知直线l₁的倾斜角=15°，直线l₁与l₂的交点为A，把直线l₂绕着点A按逆时针方向旋转到和直线l₁重合时所转的最小正角为60°，求直线l₂的斜率k₂．（12分）

18．已知两点P（2，－3），Q（3，2），直线ax+y+2=0与线段PQ相交，

求a的取值范围．(12分)

19．已知的定义域为（０，＋∞），且在其上为增函数，满足，，　①求；　　②试解不等式．（12分）

20．已知函数 ，若，

，（12分）

21．某工厂库存A、B、C三种原料，可用来生产甲、乙两种产品，市场调查显示其用料和可获利润等各数据如下表：

原　料 耗料 产品	A（吨）	B（吨）	C（吨）		每吨产品利润（元）
	100	125	156		（I）	（II）
甲产品每1吨	1	2	3		2000	1000
乙产品每1吨	4	3	1		1000	3000

　　　 问：(1) 若市场情况如（I），怎样安排生产才能获得最大利润?

　　 　 　(2) 若市场情况如（II），怎样安排生产才能获得最大利润？（13分）

22．某房屋开发公司用128万元购得一块土地，欲建成不低于五层的楼房一幢，该楼每层的建筑面积为1000平方米，楼房的总建筑面积(即各层面积之和)的每平方米的平均建筑费用与楼层有关，若该楼建成x层时，每平方米的平均建筑费用用f(x)表示，且f(n)=f(m)(1+)(其中n＞m,n∈N)，又知建成五层楼房时，每平方米的平均建筑费用为400元，为了使该楼每平方米的综合费用最省(综合费用是建筑费用与购地费用之和)，公司应把该楼建成几层?（13分）

参考答案

一．选择题（本大题共12小题，每小题5分，共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	C	D	A	D	A	B	D	B	B	C	B	A

二．填空题（本大题共4小题，每小题4分，共16分）

13．2 x +3y+10=0　 14．(－2,0)∪(1,2).　 15．（4，2）　16．(-∞，-4)∪(0，1)∪(1，+∞)　

三．解答题（本大题共6小题，共74分）

17．（12分）

[解析]：设直线l₂的倾斜角为α₂,则由题意知： 180°－α₂+15°=60°,α₂=135°,

∴k₂=tanα₂=tan（180°－45°）=－tan45°=－1.

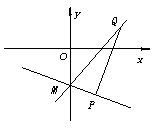18．（12分）

[解析]：如右图直线l：ax+y+2=0恒过定点M（0，－2），

l与线段PQ相交，故k_MP≤k₁≤k_MQ．

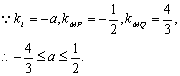
19．（12分）

［解析］：①由题意可得，，

　　　　②因为所以原不等式可化成

由题意可得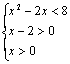， 　故不等式的解集为{x}

20．（12分）

[证明]：由题意可知，即证：

　　 左=

　　 右=

因为，只要证

又因为，>0，只要证

得1+

　　　　　　　　　　　

　　　　　　  而恒成立　 所以原不等式成立

21．（13分）

[解析]：设安排生产甲、乙两种产品的吨数分别为x，y，利润总额为z元.

　　　　 由题意得约束条件为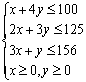　，作出可行域如图.

　　　　 （1）若市场情况如（I），则目标函数

作直线.

　　　　 　 把l₁向右上方平移到l₁′的位置时，直线经过可行域

上的点C，且与原点距离最大，此时z取得最大值.

 解方程组.此即所求最优解.

（2）若市场情况如（II），则目标函数

，即，

把l₂向右上方平移至l₂′的位置时,直线经过可行域上的点B,且与原点距离最大，此时z取得最大值，

解方程组此即所求最优解.

答：（1）若市场情况如（I），应生产甲、乙产品分别为49吨和9吨.

　　　 （2）若市场情况如（II），应生产甲、乙产品分别为40吨和15吨.

22．（13分）

[解析]：设该楼建成x层，则每平方米的购地费用为＝ 　　　 

由题意知f(5)＝400,　f(x)＝f(5)(1+)＝400(1+)　　　　　　　　 

　从而每平方米的综合费用为y=f(x)+＝20（x+）+300≥20×2+300＝620（元），当且仅当x=8时等号成立　　　　　　　　　　　　　　　　　　　　　　

 故当该楼建成8层时，每平方米的综合费用最省.