高二数学期中试卷
一. 选择题（45分）
（1）等差数列
中，
，则
的值为（ ）
A. 3 B.
（2）设是公差为-2的等差数列，如果
，则
等于（ ）
A. 182 B. -82 C. -80 D. 180
（3）抛物线
的准线方程是（ ）
A. 
B.
C.
D.
（4）一动圆与两圆
和
都外切，则动圆圆心轨迹为（ ）
A. 圆 B. 椭圆 C. 双曲线的一支 D. 抛物线
（5）若
，则实数m等于（ ）
A. 
B.
C.
D.
1或2
（6）若将20，50，100各加上相同的常数，组成等比数列，则其公比为（ ）
A. 
B.
C.
D.
（7）
（ ）
A. 0 B.
1 C.
D.
3
（8）一个等比数列中，
，则
等于（ ）
A. 183 B. 108 C. 75 D. 63
（9）
，则
的取值范围是（ ）
A. 
B.
C. 
D.
（10）椭圆
的两焦点
，过
引直线L交椭圆于A、B两点，则
的周长为（ ）
A. 5 B. 15 C. 10 D. 20
（11）若抛物线
与
有公共焦点则（ ）
A. 
B.
C. 
D.
（12）到A（-1，0）和直线x=3的距离相等的点的轨迹方程为（ ）
A. 
B.
C. 
D.
（13）若z为复数且
，则
的最大值为（ ）
A. 1 B.
C.
D.
（14）若椭圆的短轴、焦距、长轴的长度依次成等差数列，则这个椭圆的离心率为（ ）
A. 
B.
C.
D.
（15）已知双曲线
的右焦点为F，点A（9，2），在双曲线上有一点M，使
的值最小，则最小值是（ ）
A. 
B.
C
D.
二. 填空题（15分）
（16）已知a、b、c成等比数列，公比为3，且a、b+8、c成等差数列，则b=_____。
（17）计算机的成本不断降低，若每隔5年价格降低
，现在价格8100元，计算机15年后的价格为__________。
（18）在等比数列中，
，则
_______。
（19）双曲线
的焦距是___________。
（20）顶点在原点，焦点在x轴的负半轴上的抛物线被直线
截得的弦长为
，则抛物线方程是__________________。
三. 解答题（40分）
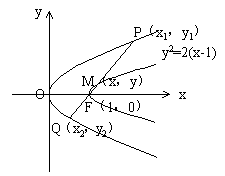
（21）过抛物线
的焦点作直线与此抛物线相交于两点P和Q，求线段PQ中点的轨迹方程。
（22）已知
，且
，求实数a、b的值。
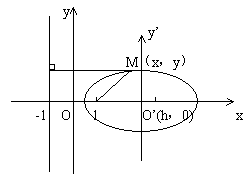
（23）已知椭圆的率心率
且左焦点与左准线分别为抛物线的焦点和准线，求此椭圆方程。
（24）数列中，已知
，
①求出
。
②猜想数列的前n项和
的公式，并加以证明。
③求
的值。
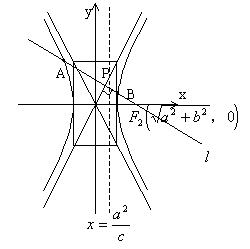
（25）已知双曲线
，过右焦点F作第一、三象限的渐近线的垂线
，垂足为P，且在双曲线左右两支的交点为A、B。
①求证：点P在双曲线的右准线上。
②求双曲线离心率的取值范围。
【试题答案】
一. 选择题。
（1）C （2）B （3）C （4）C （5）B
（6）A （7）C （8）D （9）C （10）D
（11）A （12）A （13）D （14）B （15）B
二. 填空题。
（16）12 （17）2400元 （18）9
（19）10 （20）
三. 解答题。
（21）略解：设线段PQ中点M（x，y）为所求轨迹上任意一点
（k存在）交抛物线于P（x，y），Q（x2，y2）两点
则
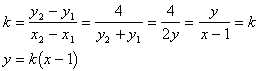
为所求
而k不存在时，PQ的中点为（1，0），亦在
上
（22）解：
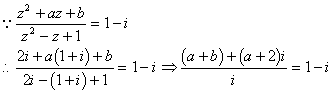
即
为所求
（23）解：
抛物线
设M（x，y）为所求轨迹上任意一点，且
则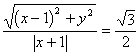
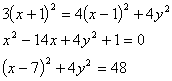
即
为所求
（24）解：①
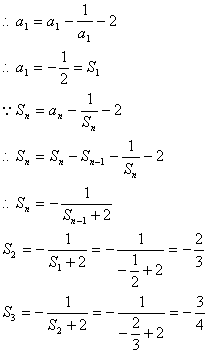
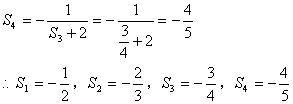
②猜想：
对证明如下：
<1>当
时，已证：
<2>设
，原命题成立
即
当
时，
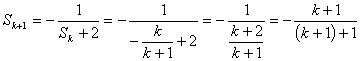
时，原命题成立
由<1>、<2>可知对任意
，原命题都成立
③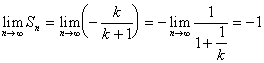
（25）略解：①的右焦点F（c，0）
即
该双曲线在第一、三象限的渐近线方程为
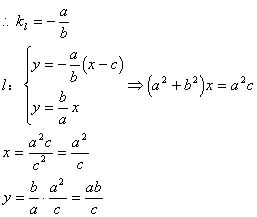
在直线
上，而双曲线右准线为
即P点在双曲线的右准线上
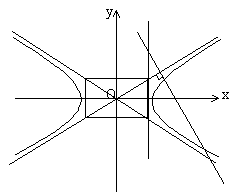
②过双曲线右焦点F作双曲线左右两支的交点为A、B
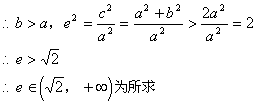
| 年级 | 高二 | 学科 | 数学 | 版本 | 期数 | ||||||||
| 内容标题 | 北京101中学高二数学期中试卷 | ||||||||||||
| 分类索引号 | G.624.6 | 分类索引描述 | 考试试题与题解 | ||||||||||
| 主题词 | 北京101中学高二数学期中试卷 | 栏目名称 | 名校题库 | ||||||||||
| 供稿老师 | 审稿老师 | ||||||||||||
| 录入 | 李红英 | 一校 | 康纪云 | 二校 | 审核 | ||||||||