高二数学期终考试试题
一. 选择题: 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中,只有一项是符和题目要求的.
(1)直线的倾斜角
的取值范围是( ) .
A . 0
<<
B . 0 
C .0 
D .0 
<
(2)方程{
x = a
+ r cos
y = b
+ r sin
( 为参数 )表示的曲线是 (
).
A .椭圆 B.圆 C.双曲线 D.抛物线
(3)等轴双曲线的离心率等于( ).
A. 1
B. 
D.
(4)给出下列四个命题:
①如果a > b,那么a – c > b – c ;②如果a > b ,那么
>
③如果a > b, c > d,那么ac ＞ｂｄ；④如果
＞ 
，那么ａ＞ｂ．
其中真命题的个数为（ ）．
Ａ．１ Ｂ． ２ Ｃ． ３ Ｄ． ４
（５）椭圆
＋２
＝４的准线方程是 （ ）．
Ａ．ｘ＝，ｘ＝－ Ｂ．ｘ＝ ，ｘ＝－
Ｃ．ｘ＝２，ｘ＝－２ Ｄ．ｘ＝
，ｘ＝－
（６）若ａ＝２－
，ｂ＝－２，ｃ＝５－２，则 （ ）．
Ａ． ｂ＜ａ＜ｃ Ｂ．ａ＜ｃ＜ｂ Ｃ．ｃ＜ａ＜ｂ Ｄ．ａ＜ｂ＜ｃ
（７）双曲线－
＝－１的焦点坐标是 （ ）．
Ａ．（０ ，２），（０ ，－２） Ｂ．（２ ，０），（－２，０）
Ｃ．（０ ，），（０ ，－） Ｄ．（０， ４），（０，－４）
（８）若直线（１＋ａ）ｘ＋ｙ＋１＝０与圆+－２ｘ＝０相切，则ａ的值为（ ）．
Ａ．1,－１ B.2 ,- 2 Ｃ．1 Ｄ．－1
（９）椭圆５ ＋ｋ＝５的一个焦点是（０，２），则ｋ＝（ ）．
Ａ．－１ Ｂ．１ Ｃ． Ｄ．－ （１０）若ａ＞ｂ＞１，Ｐ＝
Ｑ＝
，Ｒ＝ｌｇ（
）
则 （ ）．
Ａ．Ｒ＜Ｐ＜Ｑ Ｂ．Ｐ＜Ｑ＜Ｒ Ｃ．Ｑ＜Ｐ＜Ｒ Ｄ．Ｐ＜Ｒ＜Ｑ
（１１）已知两条直线l
:y = x, l
: ax –y = 0,其中a 为实数,当这两条直线的夹角在(0 ,
)变动时,a的取值范围是( ).
A.(0
,-1) B.(
) C.
(
) D.
(1, 
)
(12)过抛物线y =2的焦点F作一直线,交抛物线与M , N两点.若线段MF 与FN 的长分别是m ，ｎ，则
（ ）．
Ａ．４ Ｂ．
Ｃ．８ Ｄ．２
二．填空题：本大题共４小题，每小题４分，共１６分．把答案填在题中横线上．
（１３）电影放映机的聚光灯有一个反射镜，它的形状是旋转椭圆面．为了使片门（电影胶片通过的地方）处获得最强光线，灯丝与片门应位于椭圆的两个焦点处，这是利用＿＿＿＿＿＿＿＿＿＿＿的一个实例．
（１４）如果ａ，ｂ
，且ａ≠ｂ，则
与
的大小关系是＿＿＿＿＿＿＿＿＿＿＿．
（１５）与两圆
及
都外切的圆的圆心在＿＿＿＿＿＿＿＿＿＿＿＿＿上．
（１６）若
，则
的最大值是＿＿＿＿．
三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)已知抛物线的顶点在原点,焦点在y轴的负半轴上, 且抛物线上一点P(m , -3 )到焦点F的距离为5. 求这个抛物线的方程.
(18)(本小题满分12分)解不等式:
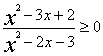
(19)(本小题满分12分)
要将两种大小不同的钢板截成A ,B ,C 三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
| 规格类型 钢板类型 | A规格
|
B规格
|
C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
今需要A ,B ,C三种规格的成品分别为15 ,18 ,27 块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少.
(20)(本小题满分12分)已知 a > 0 , b > 0 , 2c > a + b.求证
c - 
< a < c + .
(21)(本小题满分14分)已知椭圆 C1 :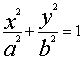
( a > b > 0 )的一条准线方程是 x =
,其左 ,右顶点分别是
A , B ;双曲线 C2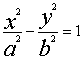 
的一条渐近线方程为 3x – 5y = 0 .
(1)求椭圆 C1的方程和双曲线C2的离心率 ;
(2)在第一象限内取双曲线C2上一点P ,连接AP交椭圆C1于点M ,连接PB并延长交椭圆C1于点N ,若点M恰为线段AP的中点, 求证MN ┷ AB .
(22)(本小题满分12分, 附加题8分)
(Ⅰ)某小区欲建一面积为640
的距形绿地,四周有小路,绿地长边外小路宽
(Ⅱ) (附加题, 答对加8分,但全卷总分不超过150分)
如果将640改为a (
a 
), 并界定绿地长边至多
怎样设计绿地的长宽使绿地和小路总占地面积最小?
2003年高二数学期终考试试题解答
一.(1)D (2)B (3)D (4)B (5)C (6)D (7)A (8)D (9)B (10)B (11)C (12)C
二.(13)椭圆光学性质 (14) > 
b +a
(15)双曲线的一支上
(16) -
三.(17)解: 依题意可设抛物线方程为 
, 由抛物线的定义得
p =4.
所以, 这个抛物线方程为
(18)解: 原不等式等价于
{
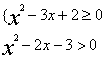或
{
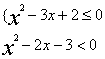
(x-1)(x-2)
或
{(x-1)(x-2)
{ (x-3)(x+1)>0 {(x-3)(x+1)<0
{
或
{ 
x < 1 或x >
3
或 1
.
故原不等式解集为 { x ∣x < - 1或 1 或 x >3 }.
(19)解: 设需截第一种钢板x张, 第二种钢板y张, 则有
2x + y 
,
x
+ 2y 
,
x +3y 
,
x ,
y .
作出可行域(略)
目标函数为
z =x +y,
作出一组平行线
x + y =t,
其中经过可行域的点且和原点距离最近的直线, 是经过x +3y =27 和 2x
+ y =15的交点 ( 
, 
)的直线
x + y =
,
而可行域内点 (
不是最优解.
经过可行域内的整点且与原点最近的直线是
x + y =12,
经过的整点 B( 3, 9 )和 C( 4,8 )是最优解.
答: 满足条件的截法有两种, 即第一种钢板截3 张,第二种钢板截9 张; 或第一种钢板截4 张,第二种钢板截8张.
(20)证明: 原不等式等价于
,
即
∣a
– c ∣< ,
只需证
,
即 a ( a -2c ) < - ab.
因为 a > 0, 2c > a + b 即 a -2c < - b ,
所以 a ( a – 2c ) < - ab ,
故原不等式成立.
(21)解:(1) 因为椭圆C1的准线方程为 x =, 所以 
.
因为双曲线C2
的渐近线方程为 y =
, 所以
.
有 a =5 , b =3.
所以, 椭圆C1 的方程为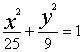
, 双曲线C2 的离心率
e =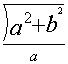
= 
.
(2)设P ( x0 ,y0 ), ( x0 > 5, y0 > 0 ),则有 M (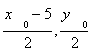
).
因为M在椭圆C1上, P在双曲线C2 上,
所以
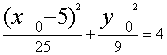① 
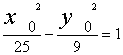②
①+ ② ,得 x0 = 10 或 x0 = - 5 ( 舍 ).
所以 P ( 10, 3 ) ,M
( 
).
lpN :
y = 
,
代入椭圆C1 的方程, 得
2x2 -15x + 25 = 0,
解得 
或 
(舍 )
又
, 故MN┷AB
( 22).解:( Ⅰ )设绿地的长为x m ( x > 0 ),则宽为
m,总占地面积为 S ,
S = ( x + 16 )( + 10 )
=
10 ( x + 
) + 800
+ 800
=1440,
当且仅当 x = 即 x = 32 时,上式取等号.此时 
.
故当绿地长宽分别为.
( Ⅱ )设绿地长为x m( x > 0 ), 则宽为
m,且x > , 总占地面积为S ,
S = ( x + 16 )(
=10x +
+ a +160
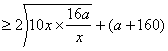
= 8
,
当且仅当 10x = , 即x =
时,上式取等号.
满足等号成立的充要条件
. 20
,
.
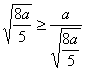即
250
又依条件 300 
, 得
当300 
, 取x =时, S有最小值. 此时长为 m ,宽为
m .
当 490 < a ,
设 u(x) =10x +
,
u(x) – u(28) =10x +
=(28 – x)
,
这是因为 20
, a > 490
使得 28 – x 
因此, 当x =28 时, S 有最小值, 并注意到此时 
< 28 ( a ).
三 2003
