期末复习(一)
教学目标:
要较好地掌握本学期学过的基础知识,解题的基本方法和基本技能;掌握一定的解题技巧和数学思想方法;注意培养和训练自己的计算能力。恒等变形能力和逻辑推理能力;在综合训练的基础上提高分析问题和解决问题的能力。
二. 重点与难点:
重点:
1. 曲线与方程的概念,求曲线方程的一般步骤。
2. 圆的方程(包括:标准方程、一般方程、参数方程)
直线和圆的位置关系,圆与圆的位置关系;
3. 用待定系数法求圆的方程。
难点:
1. 求曲线方程的方法的掌握,及第5步骤的查漏补缺工作的判断与处理。
2. 对圆的方程的理解及圆的知识的综合应用。
说明:1. 第六章知识是在期中考试前讲的,由学生自己复习一下;
2. 第七章内容,期中前讲了§7.1~§7.4,期中考试以后又讲了§7.5~§7.7,下面给出第七章的知识小结,但重点分析讲解§7.5~§7.7内容的题型。
教学过程:
第七章
知识总结:
知识体系表解
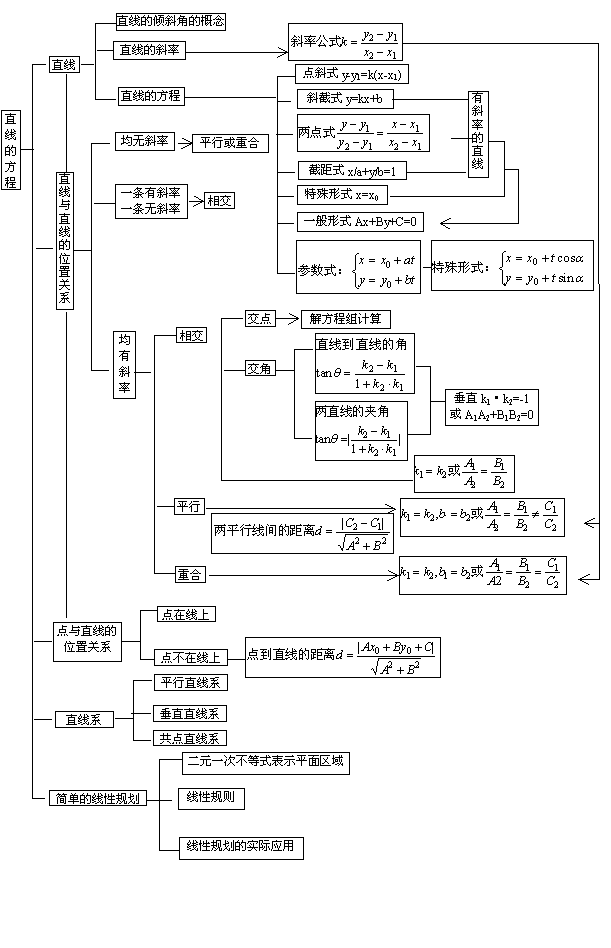
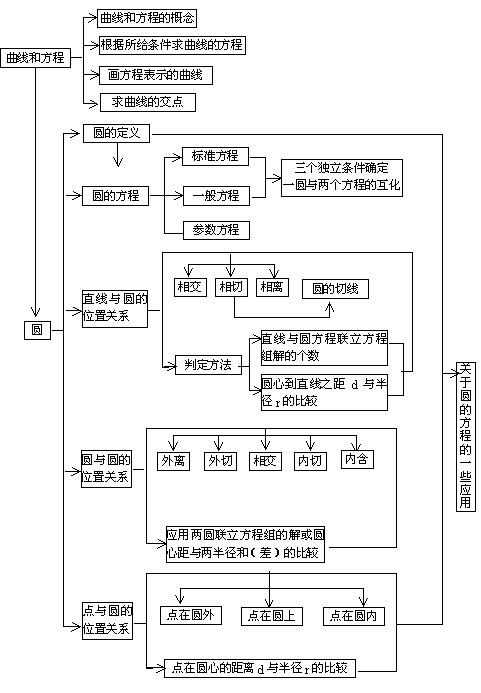
二. 典型例题分析:
例1. 选择题:
1. 点P(2,5)关于直线x+y=0的对称点的坐标是( )
A. (5,2) B. (2,-5)
C. (-5,-2) D. (-2,-5)
![]()
A. 圆 B. 点 C. 直线 D. 椭圆
![]()
![]()
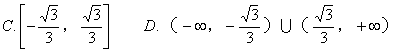
![]()
A. 5 B. 25 C. 9 D. 3
解:1. ∵点P(2,5)关于直线x+y=0对称,设对称点为P′
∴直线x+y=0应是线段PP′的中垂线,∴PP′的中点应在x+y=0上,用代值法排除(A)(B)
再用斜率kPP′=1,排除(D)∴选(C)。
解:2. 把方程配方:2(x-1)2+(y+1)2=0
若两个非负数的和为零,则应它们同时为零。
![]()
解:3. 先把参数方程化为普通方程:(x-2)2+y2=1
![]()
![]()
推出y=kx
问题转化为求斜率k的取值范围。
![]()
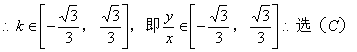
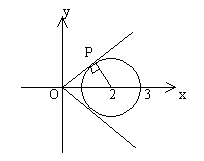
解:4. 先求出已知圆的图形
设x2+y2=r2
![]()
上式表示点P(x,y)到原点的距离
又∵点P在已知圆上,∴观察已知,连接OC时与圆C的交点到原点的距离最小。
![]()
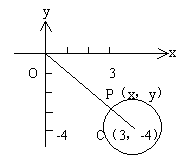
例2. 填空题:
1. 点M(x0,y0)是圆x2+y2=a2(a>0)内不为圆心的一点,则直线x0x+y0y=a2与该圆的位置关系为__________________。
![]() 围是______________。
围是______________。
3. 过点P(2,4),作圆(x-1)2+(y-1)2=1的切线,则圆的切线方程是______________。
解:1. 判断直线与圆的位置关系,应看圆心到直线的距离与圆的半径的大小关系即可。
![]()

![]()
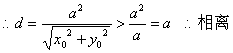
解:2. 数形结合为最佳方法:
![]()
![]()
y=x+b表示一簇与y=x平行的直线,当y=x向上运动到b=1时,直线与曲线有两个交![]()
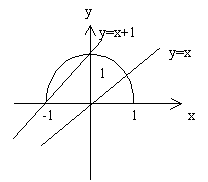
解3:∵点P(2,4)在圆外
∴过点P与圆相切的直线有两条,当斜率存在时,设方程为y-4=k(x-2)
![]()
圆心(1,1)
∵圆心到切线的距离等于半径
![]()
![]()
当斜率不存在时,过点P(2,4)的直线为:x=2
∴所求圆的切线方程为:4x-3y+4=0或x=2

例3. (1)已知圆过点P(2,1),与直线x-y=1相切,且它的圆心在直线y=-2x上,求这个圆的方程。
![]()
x-3y=0上,求此圆的方程。
解:(1)设所求圆的方程为:(x-a)2+(y-b)2=r2
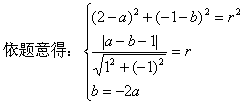
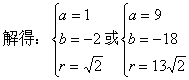
![]()
解:(2)设所求圆的方程为:(x-a)2+(y-b)2=r2
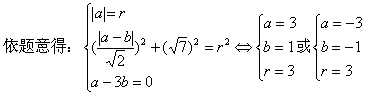
![]()
例4. ![]()
![]()
求点P的轨迹。
解:设P(x,y)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
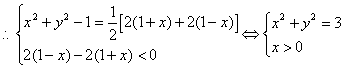
![]()
【模拟试题】
1. 已知:x、y满足x+3y-10=0,则x2+y2的最小值为______________
![]() 求动点Q的轨迹方程。
求动点Q的轨迹方程。
3. 自点P(-3,3)发出的光线l经x轴反射,其反射线所在直线正好与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程。
4. 求经过直线x=-2与已知圆x2+y2+2x-4y-11=0的交点的所有圆中,具有最小面积的圆的方程。
【试题答案】
![]()
![]()
又∵点(x,y)满足x+3y-10=0,∴(x,y)在直线上。
∴题意为:在直线x+3y-10=0上求一点使它到原点距离最小,数形结合即可找到。
![]()
![]()
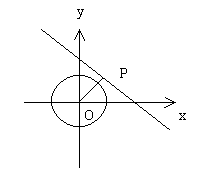
2. 设Q(x,y),P(x1,y1)
![]()
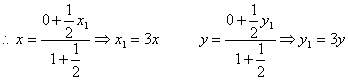
![]()
即:2x+4y+1=0为所求Q点的轨迹方程。
3. 已知圆C的方程化为:(x-2)2+(y-2)2=1
设光线l的方程为:y-3=k(x+3),由题意知k≠0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

4. 分析:过两定点的所有圆中,面积最小的圆是以这两点的连线为直径的圆。因此,只须求出交点,便可确定所求圆的圆心和半径。
解: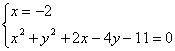
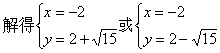
![]()
![]()
![]()
![]()
![]()