高二数学第一学期教学质量检测试卷5
第Ⅰ卷（选择题）
(本试卷满分100分，在100分钟内完成)
一、选择题：（本题共12小题，每小题3分，满分36分）
在每小题给出的四个答案中，只有一个答案是正确的，请将正确的答案选出来，将其代号填写在下表中对应的题号下.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1. 若a，b，c∈R，且a>b，则下列不等式中一定成立的是
A、ac>bc B、ac2>bc2 C、a2>b2 D、c-b>c-a
2.“x<1”是“
”成立的
A、充分但不必要条件 B、必要但不充分条件
C、充要条件 D、非充分非必要条件
3. 若0<a<1，0<b<1，把a＋b，2
，2ab，a2＋b2中最大与最小者分别记为M和m，则
A、M＝a＋b，
m＝2ab
B、M＝a2＋b2， m＝2
C、M＝a＋b，
m＝2
D、M＝a2＋b2， m＝2ab
4.不等式
—3＜1的解集是
A、{x5＜x＜16} B、{x6＜x＜18}
C、{x7＜x＜20} D、{x8＜x＜22}
5.过点(1，0)，斜率为1的直线方程是
A、x-y-1=0 B、y=x+1 C、x+y=1 D、x+y+1=0
6.设点P在有向线段
的延长线上，P分所成的比为
，则
A、 <-1 B、-1<<0 C、0<<1 D、
>1
7.如果直线ax+y+1=0与直线3x-y-2=0平行，那么系数a为
A、-3 B、-6
C、-
D、
8.已知x、y满足约束条件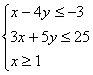
，则z=x+2y的最大值为
A、12 B、
C、9 D、3
9. 圆
上的点到直线2x－y＋1＝0的最短距离是
A、
－1
B、3－
C、－2
D、2
10. 椭圆
=1的离心率为
A、
B、
C、
D、
11.如果抛物线y2=2px
上的点M(x0，8)到焦点的距离为10，则p等于
A、4 B、16 C、8或32 D、4或16翰林汇
12.如果双曲线的两条准线分两焦点间的线段为三等分，则此双曲线的离心率是
A、3
B、 C、
D、
翰林汇
第Ⅱ卷（非选择题）
二、填空题（本题共4小题，每小题3分，共12分）
13. 不等式
＞0的解集是 .
14. 不等式x2+（m—2）x+（5—m）＞0对任意实数x都成立，则实数m的取值范围为 .
15.两直线
和x=1 夹角的平分线方程是
.
16.若m∈R，圆x2＋y2－2mx＋4my＋5m2－1＝0＝0的圆心的轨迹方程是 .
三、解答题（本题满分52分）
17.（本题满分8分）求点（—2，3）关于直线y=x+1对称的点的坐标.
18. （本题满分8分）已知椭圆中心在坐标原点，焦点在x轴上，离心率
，且椭圆过点A（5，4），求椭圆方程。
19. （本题满分8分）求直线y= 
x+1被双曲线
=1截得的弦长.
20. （本题满分8分）建造一个容积为8m3，深为2m的长方体无盖水池. 如果池底和池壁的造价每平方米分别为120元和80元, 那么水池的最低总造价为多少？
21.（本题满分10分）解关于x的不等式
.(a>0，且a≠1)
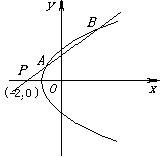
22.（本题满分10分） 已知直线
的斜率为k（k≠0），且过点P(－2，0)，抛物线C： y2=4(x+1).直线与抛物线C有两个不同的交点A、B，
(1)求k的取值范围;
(2)直线的斜率为何值时，A、B与抛物线C的焦点的连线互相垂直.
参考答案
一、选择题
1.D 2.B 3.A 4.B 5.A 6.A 7.A 8.B 9.C 10.A 11.D 12.D
二、填空题
13. {x x＜—1或1＜x＜3} 14.—4＜m＜4
15. 
16. y= 2x
三、解答题
17.解：过点（—2，3）且与直线y=x+1垂直的直线方程为：
y—3= —（x+2）----------------------------------------------------------------------2分
即 y= —x+1
联解方程
得两直线的交点为（0，1）-------------------------------------5分
根据中点坐标公式可得所求点的坐标为（2，—1）.----------------------------------8分
18.解：依题意可设所求椭圆方程为：
+
=1----------------------------------------2分
∵ c2=a2—b2 -----------------------------------------------------------------------------------3分
∴
根据题设可知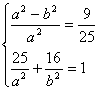
-----------------------------------------------------------5分
解之得 a2=50，b2=32，------------------------------------------------------------------------7分
∴所求椭圆方程为：
+
=1.---------------------------------------------------------------8分
19.解：将直线y= x+1代入双曲线=1中并整理得：
x2—4x—12=0--------------------------------------------------------------------------2分
解之得： x1= —2，x2=6
进而可得：y1=0， y2=4---------------------------------------------------------------------5分
∴弦长d=
------------------------------------------------------6分
=
=4.--------------------------------------------------------------------------------------7分
∴直线y= x+1被双曲线=1截得的弦长为4.------------------------8分
20.解：设长方体的长为xm，宽为ym，总造价为p元.
则 p=120xy+80（4x+4y）-----------------------------------------------------------------2分
又∵2xy=8
∴ p=480+80（4x+
）--------------------------------------------------------------------4分
≥480+80·2
=1760--------------------------------------------------------------------------------------6分
当且仅当4x=即x=2时，p最低.-------------------------------------------------------7分
∴ 当水池是棱长为2m的正方体时，总造价最低为1760元.------------------------8分
21. 解：（1）当a>1时,原不等式化为: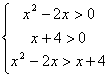
---------------------------2分
-4<x<-1或x>4
---------------------------------------------------------------------5分
（2）当0<a<1时,原不等式化为: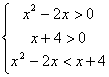
-----------------------------7分
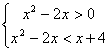
-1<x<0或2<x<4 ----------------------------------------------9分
综上可知,当0<a<1时,不等式的解为-1<x<0或2<x<4 -------------------------------10分
22. 解：(1)直线的方程为y=k
(x+2) ①----------------------1分
将①代入抛物线方程整理得
k2x2+4(k2－1)x+4(k2－1)=0 ②----------------------2分
∵与C有两个不同的交点，∴
，-----------------------------------------------3分
即 16(k2－1)2－16k2(k2－1)＞0，解得 －1＜k＜1.--------------------------------------4分
∴当－1＜k＜1且k≠0时，与C有两个不同的交点.--------------------------------5分
(2)设A(x1，y1)，B(x2，y2)，抛物线的焦点为O(0，0)
由OA⊥OB得 x1x2+y1y2=0 ③----------------------6分
由②可得 
；
④----------------------7分
=[k(x1+2)][k(x2+2)]=k2[x1x2+2(x1+x2)+4]
，
即 y1y2=4 ⑤------------------------8分
将④,⑤代入③得， 
，解得
.-------------------------9分
∴当 时, OA⊥OB.--------------------------------------------------------------10分