高二数学第一学期教学质量检测试卷
第Ⅰ卷(选择题)
(本试卷满分150分,在120分钟内完成)
一、选择题:(本题共10小题,每小题6分,满分60分,请将答案直接填在下表中)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1. 若a,b,c∈R,则下列命题正确的是
(A)如果![]() ,那么
,那么![]() (B)如果
(B)如果![]() ,那么
,那么![]()
(C)如果![]() ,那么
,那么![]() (D)如果
(D)如果![]() ,那么
,那么![]()
2. 已知x>0,则函数![]() 的最小值为
的最小值为
(A)6![]() (B)26
(C)2-4
(B)26
(C)2-4![]() (D)2+4
(D)2+4![]()
3. 已知a、b是不相等的正实数,则下列关系式中值最大的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4. 不等式![]() 的解集为
的解集为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5. 如果经过点A(m,2)、B(-m,![]() ,那么m=
,那么m=
(A)-![]() (B)
(B)![]() (C)-
(C)-![]() (D)
(D)![]()
6. 已知x、y满足约束条件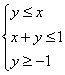 ,则z=2x+y的最小值为
,则z=2x+y的最小值为
(A)3
(B)![]() (C)-3
(D)-4
(C)-3
(D)-4
7. 已知![]() =1,则x+y的最大值为
=1,则x+y的最大值为
(A)![]() (B)1
(C)-1
(D)-
(B)1
(C)-1
(D)-![]()
8. 椭圆![]() =1上一点P到一个焦点的距离等于3,则点P到相对应的准线的距离为
=1上一点P到一个焦点的距离等于3,则点P到相对应的准线的距离为
(A)4
(B)5
(C)![]() (D)
(D)![]()
9. 双曲线![]() 的两条准线的距离等于
的两条准线的距离等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 经过抛物线![]() 焦点的直线l交抛物线于A、B两点,且AB=8,则直线l的倾斜角的大小为
焦点的直线l交抛物线于A、B两点,且AB=8,则直线l的倾斜角的大小为
(A)600 (B)450 (C)600或1200 (D)450或1350
第Ⅱ卷(非选择题)
二、填空题(本题共4小题,每小题4分,共16分)
11. 不等式3x-4≤19的解集是 .
12. 直线![]() 与直线
与直线![]() 夹角的大小是
.
夹角的大小是
.
13. 过点(2,3)且与圆![]() 相切的直线方程为
.
相切的直线方程为
.
14. 如果直线y=kx-1与双曲线![]() 没有公共点,则k的取值范围是
.
没有公共点,则k的取值范围是
.
三、解答题(本大题共6小题,满分74分)
15.(本题满分12分)
求证:![]() .
.
16. (本题满分12分)
已知点P(-1,0)与Q(1,0),且动点M满足![]() ,求点M的轨迹方程,并说明轨迹是什么图形.
,求点M的轨迹方程,并说明轨迹是什么图形.
17. (本题满分12分)
已知双曲线![]() 的两个焦点为F1,F2,点P是双曲线上一点,求使PF1⊥PF2的点P的坐标.
的两个焦点为F1,F2,点P是双曲线上一点,求使PF1⊥PF2的点P的坐标.
18. (本题满分12分)
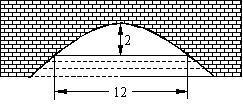
如图,抛物线形拱桥的顶点距水面
19.(本题满分12分)
已知集合A=![]() ,B=
,B=![]() .
.
(Ⅰ)当a=2时,求A![]() B;
B;
(Ⅱ)求使B![]() A的实数a的取值范围.
A的实数a的取值范围.
|
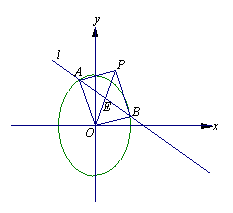
直线l:y=kx+1与椭圆C:![]() 交
交
于A、B两点,以OA,OB为邻边作平行四边形
OAPB(O为坐标原点)(如图).
(Ⅰ)当a=2,k=-1时,求AB的长;
(Ⅱ)当a=2时,求点P的轨迹方程.
参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | D | C | B | B | C | A | B | D | D |
二、填空题
11. ![]() 12. 450
12. 450
13. 3x-4y+6=0 和x=2
14.![]()
三、解答题
15. 证明:∵ ![]() ………………………………………………………4分
………………………………………………………4分
=![]()
=![]() ≥0…………………………………………………………………10分
≥0…………………………………………………………………10分
∴ ![]() ……………………………………………………………………12分
……………………………………………………………………12分
16.解:设点M的坐标为(x,y),………………………………………………………2分
由于![]() ,
,
则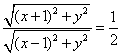 ,……………………………………………………………………6分
,……………………………………………………………………6分
整理得:![]() …………………………………………………………8分
…………………………………………………………8分
即
![]() …………………………………………………………………10分
…………………………………………………………………10分
这就是点M的轨迹方程.图形为以(-![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆.……………12分
为半径的圆.……………12分
17.解:设点P(x0,y0),因为它在双曲线上,所以
![]() ---------------------①………………2分
---------------------①………………2分
双曲线的焦点为F1(-5,0),F2(5,0),……………………………………………6分
∵ PF1⊥PF2,
∴
![]() ---------------②………………8分
---------------②………………8分
解由①、②两式组成的方程组,得
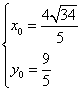 或
或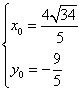 或
或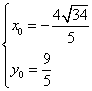 或
或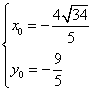 …………………10分
…………………10分
∴ 所求的点有四个:A(![]() ),B(
),B(![]() ),C(
),C(![]() ),
),
D(![]() ).………………………………………………………………………12分
).………………………………………………………………………12分
18. 解:以拱桥的顶点为原点,水平方向为x轴建立直角坐标系,
设拱桥抛物线方程为![]() (p>0),……………………………………………2分
(p>0),……………………………………………2分
∵
拱顶离水面
∴ 62=-2p·(-2),p=9,
即抛物线方程为![]() ………………………………………………………………6分
………………………………………………………………6分
又∵水面上升
x2=-18·(-1),即x=±3![]() ,…………………………………………………10分
,…………………………………………………10分
故这时水面宽为![]() m
m
19. 解:(Ⅰ)当a=2时,A=(2,7),B=(4,5)………………………………2分
∴ A![]() B=(4,5).………………………………………………………………………4分
B=(4,5).………………………………………………………………………4分
(Ⅱ)∵ B=(
当a<![]() 时,A=(
时,A=(
要使B![]() A,必须
A,必须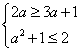 ,此时a=-1;………………………………………7分
,此时a=-1;………………………………………7分
当a=![]() 时,A=
时,A=![]() ,
,
使B![]() A的a不存在;……………………………………………………………………9分
A的a不存在;……………………………………………………………………9分
当a>![]() 时,A=(2,
时,A=(2,
要使B![]() A,必须
A,必须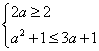 ,此时1≤a≤3.……………………………………11分
,此时1≤a≤3.……………………………………11分
综上可知,使B![]() A的实数a的取值范围为[1,3]∪{-1}……………………………12分
A的实数a的取值范围为[1,3]∪{-1}……………………………12分
20. 解:(Ⅰ)当a=2,k=-1时,
联立方程组得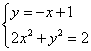 ,解之得
,解之得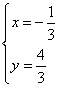 或
或![]() ,…………………………3分
,…………………………3分
即A、B的坐标分别为(![]() )和(1,0)
)和(1,0)
∴ AB=![]() .……………………………………………………6分
.……………………………………………………6分
(也可利于弦长公式计算)
(Ⅱ)设P(x,y),A(x1,y1),B(x2,y2),则E(![]() ).
).
由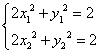 ,两式相减并整理得:
,两式相减并整理得:![]() ,……………………8分
,……………………8分
即![]() ,
,
由于l过定点M(0,1),即![]() ,
,
∴
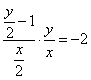 ,…………………………………………………………………………12分
,…………………………………………………………………………12分
即 ![]() ,这就是点P的轨迹方程.…………………………………………14分
,这就是点P的轨迹方程.…………………………………………14分
注:本参考答案只给出一种解法,其他