高二数学第一学期期末考试试题2
说明：（1）试卷分试题卷，答案卷两部分，试题共4页，答卷共6页；
（2）考生必须将班级、姓名、坐号填写在答案卷指定的位置上；解答内容应填写在答案卷相应的位置，否则，答卷无效；
（3）考试结束后，考生只须交回答卷，试题部分不用交．
一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有
一项是符合题目要求的，请将正确答案填在答题卷相应的位置上．）
1、若
且
，则有
（A） 
（B） 
（C） 
（D） 
2、方程
表示的曲线是
（A） 一条直线 （B） 一条射线 （C） 两条射线 （D） 两条直线
3、直线l1：x＋3y－7＝0，直线l２：kx－y－2＝0与x轴、y轴正向所围成的四边形有外接圆，则k的值为
（A） －3 （B） 3 （C） －6 （D） 6
4、“直线
平行于抛物线的对称轴”是“直线
与抛物线仅有一个交点”的
（A）充分不必要条件 （B）必要不充分条件
（C）充要条件 （D）不充分不必要条件
5、已知复数
则复数
的虚部为
1
i
－1
－i
6、与两圆
及
都内切的圆的圆心在
一个椭圆上
双曲线一支上
一条抛物线上
一个圆上
7、如果直线l的斜率k满足k≤1，则直线l的倾斜角的取值范围是
（A） 
（B） 
（C） 
（D） 
8、设P(x，y)是第一象限的点，且点P在直线3x＋2y＝6上移动，则xy的最大值是
（A） 1.44 （B） 1.5 （C） 2.5 （D） 1
9、若直线
和曲线
有两个交点，则
的取值范围是
（A） 
（B） 
（C） 
（D） 
10、经抛物线
的焦点作一直线l交抛物线于
、
，则
4
－4
p2
－p2
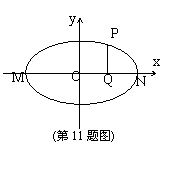11、如图，椭圆
的长轴为MN，P为椭圆上任一点，PQ⊥MN于Q且PQ2＝kMQ•QN，则k的值
等于
等于
等于1
与P的位置有关
12、设双曲线
的半焦距为c，
直线l过(a，0)，(0，b)两点，已知原点到直线l的距离为
c，则双曲线的离心率为
（A） 2
（B） 
（C） 
（D） 
二、填空题（本大题共4小题，每小题4分，共16分．请将正确答案填在答题卷相应的位
置上．）
13、实数a、b、c、d满足下列三个条件：
．则将a、b、c、d按由大到小的顺序排列为
．（不按要求作答不给分）
14、点
到直线
的距离等于4，且不在不等式
表示的平面区域
内，则点P的坐标为 ．
15、双曲线
的两条渐近线的夹角是
．
16、给出下列四个命题：
①平行直线
和
的距离是
；
②方程
不可能表示圆；
③双曲线
的离心率为
，则k的取值范围是
；
④曲线
关于原点对称．
其中正确的命题的序号是 ．
三、解答题（本大题共6小题共48分．解答应写出文字说明，证明过程或演算步骤．请将
解答过程写在答题卷相应的位置上．）
17、（本小题满分6分）
解关于x的不等式：
．
18、（本小题满分8分）
△ABC的边AB为定长c，若边BC的中线为定长r，试求顶点C的轨迹方程．
19、（本小题满分8分）
椭圆的离心率是
，它被直线
截得的弦长是
，求椭圆的方程．
20、（本小题满分8分）
学校打印室和电脑室每学期分两次同时到印刷厂购买打印纸，每次两室购买价格相同，
但打印纸价格随时间变化，打印室每次购买3 000元打印纸，电脑室每次购买3 000张打印纸，一学期里哪个室购买打印纸的平均价格低？说明理由（平均价格＝总价值÷总张数）．
21、（本小题满分8分）
已知双曲线方程为
．过定点Q（1，1）能否作直线
，使与此双曲线相交于两点Q1、Q2，且Q是Q1Q2的中点？若存在求出的方程,若不存在，说明理由．
22、（本小题满分10分）
是抛物线上三点，其中
，并且A、B、C三点到焦点的距离成等差数列．
（1）求抛物线方程；
（2）证明：
．
第一学期期末考试
高二数学参考答案及评分标准
选择题答案（每小题3分）：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | B | A | A | B | D | B | D | B | A | A |
提示：3．“四边形有外接圆”即“四边形对角互补”，即“直线l1，l２：互相垂直”．
5．见“复数同步练习题”习题14．2选择题2．
7．由定义，可汰（C），又k存在，可汰（A），取k＝0代入，满足条件，选（D）．
8．
，（当且仅当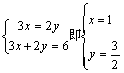
时取等号）．
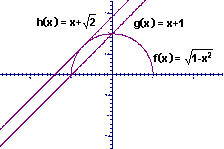
9．用数形结合法，如图．此题不能用判别式法，否则，视为判断直线和整个圆有两个交点．
10．用特殊值法．取l为通径，则
，
，
．
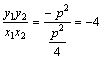11．用特殊值法．取P与短轴顶点重合，则PQ＝
，MQ＝a，QN＝a，PQ2＝kMQ•QN即
；取Q与右焦点重合，则PQ＝
，MQ＝（a＋c），QN＝（a－c），PQ2＝kMQ•QN即
．
12．直线l的方程为
，原点到直线l的距离为c，即
，解得
，或
，当时，
符合条件．
填空题答案（每小题4分）：
13、bdca 14、（7，3） 15、60O 16、①④
解答题答案：
17、原不等式等价于
①
．．．．．．
1分
（1）当
时，
，这时由①得
原不等式的解集为
．．．．．．．．．．．．．．．．．．．．．． 3分
（2）当
时，原不等式无解 ．．．．．．．．．．．．．．．．．．．．．． 4分
（3）当
时，
，这时由①得
原不等式的解集为
．．．．．．．．．．．．．．．．．．．．．． 6分
18、以AB所在的直线为x轴，A为原点建立直角坐标系， ．． 2分
如图，则点A、B的坐标分别为（0，0）、（c，0），
设点C的坐标为（x，y）． ．．．．．．．．．．．．．．．．． 3分
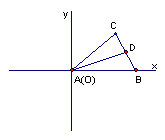设AB的中点为D（x1，y1），
∴
∴D的坐标为（
）． ．．．．．．．．．．．．．．．． 5分
又AD=r，即
．．．．． 6分
当C在AB所在的直线上时，不符合题意，即y≠0 ．．．． 7分
∴点C的轨迹方程是
．．．．．．．．．8分
19、∵
∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 2分
∴椭圆方程可写为
将直线方程代入椭圆方程，消去y，整理得
．．．．．．．．．．．．．．．．．．．． 4分
依韦达定理得
．．．．．．．．．．．．． 5分
∴
解得c＝1 ∴a2＝3，b2＝2． ．．．．．．．．．．．．．．．．．．．．．．．． 7分
∴椭圆方程为
．．．．．．．．．．．．．．．．．．．．．．．．．． 8分
20、设两次价格分别为x和y（x≠y），则 ．．．．．．．．．．．．．．．．．．．．．．．．．．． 1分
打印室购纸平均价为：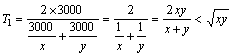
．．．．．．．
4分
电脑室购纸平均价为：
．．．．．．．．．．． 7分
∴打印室购纸平均价格较低． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 8分
21、假设这样的直线
存在,设
,
,
则有
,
, ．．．．．．．．．．．．．．．．．．．．．．．． 1分
又
、
在双曲线上,∴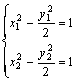
, ．．．．．．．．．．．．．．．．．．．．．．． 2分
两式相减得
,
即
,
∴
.
．．．．．．．．．．．．．．．．．．．．．．． 3分
若直线
没有斜率,则
不可能是 的中点, ．．．．．．．．．．．．．．． 4分
所以直线
有斜率,于是斜率
.
直线的方程为
,即
．．．．．．．．．．．．．．．．．．．．． 5分
将其代入得
,
∴△=16-24<0, ．．．．．．．．．．．．．．．．．．．．．． 7分
这就是说,直线与双曲线没有公共点,
∴这样的直线不存在. ．．．．．．．．．．．．．．．．．．．．．．． 8分
22、（1）由抛物线的定义，A、B、C三点到焦点的距离分别为
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 2分
依题意得
解得
．
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 3分
将
代入
，得
， ．．．．．．．．．．．．．．．．．．．．．．．． 4分
所以抛物线方程为
． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 5分
（2）因为，所以
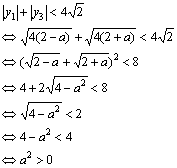．．．．．．．．．．．．．．．．．．．．．．．． 4分
而这是显然成立的，所以成立． ．．．．．．．．．．．．． 5分
附：考点分布情况
| 章 节 | 知 识 点 | 题 号 | 分 值 | 备 注 |
| 不等式 | 1、不等式的性质 | 13 | 29 | |
| 2、均值不等式 | 8、20 | |||
| 3、不等式的证明 | 22（2） | |||
| 4、不等式的解法 | 17 | |||
| 5、含绝对值不等式 | 1、 | |||
| 直线和圆 | 6、倾斜角、斜率 | 7、 | 68 | |
| 7、直线方程 | （21） | |||
| 8、两直线的位置关系 | 3、 | |||
| 9、线性规划 | 14、 | |||
| 10、曲线与方程 | 2、18 | |||
| 11、圆 | （6、9） | |||
| 圆锥曲线 | 12、椭圆 | 11、19 | ||
| 13、双曲线 | 12、15、 | |||
| 14、抛物线 | 10、22（1） | |||
| 15、直线与圆锥曲线 | 4、9、 | |||
| 16、圆锥曲线综合 | 6、16、21 | |||
| 复数 | 17、复数 | 5 | 3 | |
| 100 |