高二数学第一学期期末练习（三）
一．选择题：
1．方程x2+y2+2ax－2ay=0表示的圆（ ）。
（A）关于直线y=x对称 （B）关于直线x+y=0对称
（C）过原点且圆心在x轴上 （D）过原点且圆心在y轴上
2．椭圆
(a>b>0)的左焦点到左准线的距离是
（A）a－c （B）a－b （C）
（D）
3．双曲线
的离心率e∈(1, 2)，则k的取值范围是
（A）(0, 6) （B）(3, 12) （C）(1, 3) （D）(0, 12)
4．抛物线y=x2上的点到直线2x－y=4的最短距离是
（A）
（B）
（C）
（D）
5．双曲线
上的点P到点(5, 0)的距离是15，则点P到点(－5, 0)的距离是
（A）7 （B）23 （C）5或25 （D）7或23
6．椭圆
上的点M到焦点F1的距离是2，N是MF1的中点，则ON为
（A）4 （B）2 （C）8 （D）
7．已知0<r<
+1，则两圆x2+y2=r2与(x－1)2+(y+1)2=2的位置关系是
（A）相切 （B）相交 （C）外离 （D）内含
8．若AB是抛物线y2=18x的一条过焦点F的弦，AB=20, AD、BC垂直于y轴，D、C分别为垂足，则梯形ABCD的中位线的长是
（A）5 （B）10 （C）
（D）
9．从动点P(a, 2)向圆(x+3)2+(y+3)2=1作切线，则切线长的最小值为
（A）4 （B）2
（C）5 （D）
10．双曲线kx2+4y2=4k的离心率小于2，则k的取值范围是
（A）(－12, 0) （B）(－3, 0) （C）(－∞, 0) （D）(－60, －12)
11．已知曲线y=
与直线x+y－m=0有两个不同的交点，则m的取值范围是
（A）(0,－1)（B）[0,－1)（C）(－2,－1)（D）(－－1,－1)
12．设P为抛物线y=x2上的一个动点，则定点A(a, 0)关于P点的对称点Q的轨迹方程是
（A）y=
(x－a)2
（B）y=(x+a)2 （C）y=(x+2a)2 （D）y=(x+a)2
二．填空题：
13．
以椭圆
+y2=1的右焦点F为焦点，以原点为顶点做抛物线，抛物线与椭圆准线的一个交点为A，则AF=
.
14．双曲线
与椭圆
有共同的焦点，则m=
.
15．已知定点A(3, 2)在抛物线y2=2px (p>0)的内部，F为抛物线的焦点，点Q在抛物线上，当AQ+QF取最小值4时，p= .
16．已知直线y=kx+1与曲线x2－y－8=0的两个交点关于y轴对称，则这两个交点的坐标是 .
三．解答题：
17．已知抛物线的顶点在原点，焦点在y轴上，抛物线上一点(a, －3)到焦点的距离等于5，求a的值，并写出抛物线的方程，准线方程，焦点坐标。
18．半径为5的圆过点A(－2, 4)，并且以M(－1, 3)为中点的弦长为4
，求此圆的方程。
19．椭圆ax2+by2=1与直线x+y=1相交于A、B两点，若AB=2，且AB的中点C与椭圆中心连线的斜率为
，求a, b的值。
20．若抛物线y=ax2－1上存在A, B两点关于直线l: x+y=0对称，求实数a的取值范围。
21．已知圆C: x2+y2+6x－91=0及圆内一点P(3, 0)，求过点且与已知圆相内切的圆的圆心M的轨迹方程。
22．已知直线l的方程为y=mx+m2(m∈R)，抛物线C1的顶点和双曲线C2的中心都在坐标原点，且它们的焦点都在y轴上，
（1）当m=1时，直线l与抛物线C1有且只有一个公共点，求抛物线C1的方程；
（2）若双曲线C2的两个焦点和虚轴的一个端点组成的三角形的面积为8，且当m≠0时，直线l过C2的一个焦点和虚轴的一个端点，求双曲线C2的方程。
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | D | B | D | A | B | D | B | A | B | B |
二．填空题：
13． 14．
15．2
16．(3, 1), (－3, 1)
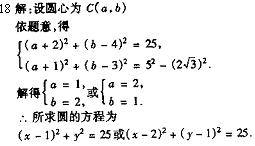
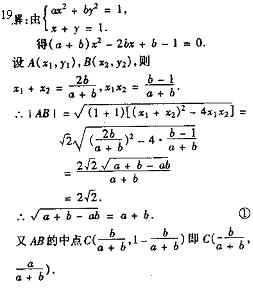
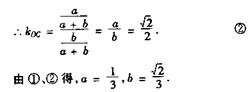
20.
