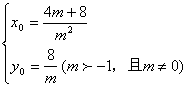高二数学第一学期期末质检复习题
一、选择题（每题3分，共36分）
1．若
，则下列不等式均成立的是（ ）
（A）
（B）
（C）
（D）
2．一个直角三角形的周长为
，其斜边长的最小值是（ ）
（1）1 （B）
（C）2 （D）
3．对于直线
，其倾斜角的取值范围是（ ）
（A）
（B）
（C）
（D）
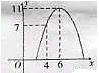4．某汽车运输公司，购买了一批豪华大客车投入营运，据市场分析
每辆客车营运的总利润
（亿元）与营运年数
为二次函数关
系如图示，则每辆客车营运多少年，其营运的年平均利润最大？（ ）
（A）3 （B）4 （C）5 （D）6
5．圆
与直线
的位置关系是（ ）
（A）相交 （B）相切 （C）相离 （D）不确定
6．与圆
外切又与
内切的圆的圆心的轨迹足（ ）
（A）两个椭圆 （B）双曲线的一支 （C）双曲线 （D）双曲线的一支和一条直线
7．设坐标原点为O，抛物线
与过焦点的直线交于A、B两点，则
等于（ ）
（A）
（B）
（C）3 （D）-3
8．双曲线
的一条准线与两条渐进线交于A、B两点，相应的焦点为F，若以AB为直径的圆恰好过F点，则双曲线的离心率为（ ）
（A）
（B）
（C）2 （D）3
9．P是长轴在x轴的椭圆
上的点，F1、F2是椭圆的两个焦点，椭圆的半焦距为c，则
的最大值与最小值之差一定是（ ）
（A）1 （B）
（C）
（D）
10．设a、b、c是△ABC的三个内角A、B、C所对的边，且lgsinA、lgsinB、lgsinC成等差数列，则直线xsin2A+ysinA-a=0与直线xsin2B+ysinC-c=0的位置关系是 （ ）
（A）平行 （B）垂直 （C）相交但不垂直 （D）重合
11．方程
表示焦点在y轴上的椭圆，则k的整数值有（ ）
（A）1个 （B）2个 （C）3个 （D）4个
12．不论
为何值，方程
的曲线都不会是 （ ）
（A）两条直线 （B）圆 （C）双曲线 （D）抛物线
二、填空题（每小题3分，共15分）
13．不等式
取等号的条件是_____________
14．两条直线
关于直线x-y=0对称，如果
的斜率为
，则
的斜率为______
15．设椭圆
的长轴两端点为M、N，P在C上，则PM与PN的斜率之积为___________
16．不等式
的解集是_________
17．若实数x、y满足x+y-4=0，则x2+y2的最小值是__________
三、解答题（18、19题每小题7分，20、21每小题8分，22题9分，23题10分，共69分）
18．已知a>0，b>0，a+b=1 求证：
19．求两直线x-3my-3=0.3mx+y+9m=0的交点的轨迹，并画出轨迹图形。
20．已知椭圆C的焦点分别为
，
，长轴长为6，设直线
交椭圆C于A、B两点，求线段AB中点坐标。
21．配制A、B两种药剂，需要甲、乙两种原料，已知配A种药需甲料3毫克，乙料5毫克；配B种药需甲料5毫克，乙料4毫克，今有甲料20毫克，乙料25毫克，若A、B两种药至少各配一剂，问共有多少种配制方法？
22．已知F1、F2为双曲线
的焦点，过F2作垂直于x轴的直线交双曲线于点P，且
PF
23．已知直线
：y=mx-4和抛物线C：y2=16x
（1）m取何值时，和C有且仅有一个公共点；
（2）若与C有两个公共点，求直线的倾斜角
的取值范围；
（3）若与C有两个公共点M和N，试用m表示MN和中点P的坐标。
参考答案
一、1.B 2.A 3.C 4.C 5.C 6.B 7.B 8.A 9.D 10.D 11.B 12.D
二、13．ab≤0 14.3 15. 16.
17.
8
三、18．略
19.所求轨迹方程为
，其圆形为圆心在原点，半径为3除去一点D（3，0）的圆。
20. 
21.区域内的整点为（1，1）、（1，2）、（1，3）、（2，1）、（2，2）、（3，1）、（3，2）、（4，1），所以在至少配一剂的情况下共有8种不同的配剂方法。
22. 
23. （1）m=0或m=-1（提示： m=0与m≠0两种情况）
（2）
或
（3）