高二数学第一学期期中考试试卷5（共四页）
命题教师：杨逸民
注：本试卷所有答案一律做在（第三、四页）答卷页上。
一． 选择题（本大题共15小题，每题3分，共45分。在每小题给出的四个选项中，只有一
项是符合题中要求的）
1. 直线2x + ay + 3 = 0的倾斜角为120°，则a的值为( )
(A)
(B) –
(C)2
(D) –2
2. 函数y = 
的定义域是 ( )
（A）x > –2 （B）x > –1 （C）x > –2 且x 
1 （D）–2 < x < –1
3. 若f(x) = 3x2 – x + 1, g (x) = 2x2 + x – 1, 则f(x)与g (x)的大小关系是 ( )
（A）f(x) > g (x) （B）f(x) = g (x)（C）f(x) < g (x)（D）随x值变化而变化
4. 过(x1，y1)和(x2，y2)两点的直线的方程是 ( )
(C) (y2 – y1)(x – x1) – (x2 – x1)(y – y1) = 0 (D) (x2 – x1) (x – x1) – (y2 – y1) (y – y1) = 0
5. 条件甲：x3 – 4x2 + 3x 
0, 条件乙：x2 – 3x + 2 0,那么甲是乙的（ ）
（A）必要但不充分的条件 （B）充分但不必要的条件
（C）充要条件 （D）既不充分又不必要的条件
6. 设a、b是满足ab < 0的实数，那么 ( )
（A）a + b > a – b （B）a + b < a – b
（C）a – b < a – b （D）a – b < a + b
7．直线l与两直线y = 1,x – y – 7 = 0分别交于P,Q两点，线段PQ中点是（1，–1），则直
线l斜率是 （ ）
(A) 
(B) 
(C) –
(D) –
8．不等式xx – 3x – 2x + 6 < 0的解区间是（ ）
（A）(3, +¥) （B）(2, 3) （C）(–¥, –3)∪(2, 3) （D）(–3, 2)∪(3, +¥)
9．设P = {x
0}, Q = {xx – 1 < a}, 若P∪Q ={xx < 5}, 则实数a的取值范
围为（ ）
（A）[1，4] （B）
（C）[3，4] （D）
10．如果点(5, b)在两条平行直线6x - 8y + 1 = 0和3x - 4y + 5 = 0之间，则b应取的整数值是 ( )
(A) – 4 (B) 4 (C) –5 (D) 5
11．点M(x, y)在直线x + 2y + 1 = 0上移动，函数z = 2x + 4y的最小值是 ( )
（A）
（B）
（C）2 （D）4
12. 两直线x2 – xy – 6y2 = 0所夹的锐角是 ( )
（A）
（B）
（C）
（D）
13. A，B是x轴上两点，点P的横坐标为2，且PA=PB，若直线PA的方程为
x–y + 1 = 0，则直线PB的方程为( )
(A) 2x – y – 1 = 0 (B) x + y – 5 = 0 (C) 2x + y – 7 = 0 (D)2y – x – 4 = 0
14. 对于任意x Î R, 
> k恒成立，则正整数k的值为 ( )
（A）1 （B）2 （C）3 （D）4
15. 若2 – m与 m – 3异号，则m的取值范围是 ( )
（A）m > 3 （B）–3 < m < 3 （C）2 < m < 3 （D）–3 < m < 2 或m > 3
二．填空题（本大题共5小题，每题4分，共20分）
16．经过点(2, –1), 方向向量为(–7, –2)的直线方程为_________.
17. 如果关于x的不等式x > 
的解集为(0, +¥), 那么实数a的取值范围为_______.
18. 点A(4, 5)关于直线l 的对称点为B(–2, 7), 则直线l的方程为____________.
19. b克糖水中有a 克糖(b > a > 0), 若再添上m克糖(m > 0), 则糖水就变甜了，试根据
这个事实提炼一个不等式___________.
20. 已知三个不等式 ① ab > 0 ② 
③ bc > ad
以其中两个作为条件，余下一个作为结论，可以组成_______个正确的命题。
三．解答题（本大题共4小题，共35分。解答应写出文字说明，证明过程或演算步骤）
21．（本小题满分7分）△ABC的顶点坐标分别为A(–3, 0), B(9, 5), C(3, 9), 直线l过点C且
把△ABC的面积分成1∶2两部分，求直线l的方程。
22．（本小题满分8分）
已知不等式x2 – 3x + a < 0的解集为{x 1 < x < b, x Î R },
(1) 求a,b的值；
(2) 解不等式 logc(–bx2 + 3x + 1 – a) < 0, 其中c > 0且c 
1.
23．（本小题满分10分）已知直线(a – 2)y = (3a – 1)x – 1.
(1)求证无论a为何值，直线总过第一象限；
(2)为使这直线不过第二象限，求a的范围。
24．（本小题满分10分）某企业决定投资生产某种产品，并用广告方式促销。已知生产这种
产品的年固定投资为10万元，每生产1万件产品还需投入18万元；又已知年销售量
（万件）与广告费
（万元）之间的函数关系为
，且已知投入广告费1万元时，可销售2万件产品。预计此种产品的年销售收入
（万元）等于年成本（万元）的150%与年广告费用50%的和。
（1）试将年利润
（万元）表示为年广告费（万元）的函数；
（2）当年广告费多少万元时，使年利润最大？年最大利润是多少万元？
四．附加题（本题满分10分，解答应写出文字说明，证明过程或演算步骤）
25．设函数f (x) = 2 x –1 –2 – x –1, x Î R. 若当0 £θ£
时, f (cos2
+ 2msin) + f(-2m–2)< 0
恒成立，求实数m的取值范围。
高二数学第一学期期中考试答卷页
一．选择题: (本大题共15小题，每小题3分，共45分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
二．填空题: (本大题共5小题，每小题4分，共20分)
16.__________________ 17.___________________ 18.____________________
19.__________________ 20.___________________
三．解答题: (本大题共4小题，21题7分，22题8分，23题10分，24题10分，共35分)
21．
22．
|
24．
四：附加题（本题10分）
25．
高二数学第一学期期中考试试卷答案
1. A 2. B 3. A 4. C 5. A 6. B 7．C 8．C 9．C 10．B 11．B 12. B
13. B 14. A 15. D
16． __2x – 7y
– 11 = 0___. 17. _
_. 18.
_3x – y + 3 = 0______
19. __
_< 
_____
20. __3__
21． 解：直线l的方程为11x – 3y – 6 = 0或17x + 6y – 105 = 0
22．解：(1) a = 2, b = 2
(2) 当c > 1时，原不等式的解集为{x 
< x < 1 }
当0 < c < 1时，原不等式的解集为f
23． 解：（1）直线系恒过第一象限内的定点(
,
)
(2) 当 a = 2时，直线x = 不过第二象限；
当 a 2时，直线方程为：y = 
x –
, 不过第二象限的充要条件为
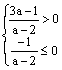
a > 2
总之，a ³ 2时，直线不过第二象限。
24．（本小题满分10分）某企业决定投资生产某种产品，并用广告方式促销。已知生产这种产品的年固定投资为10万元，每生产1万件产品还需投入18万元；又知年销售量
（万件）与广告费（万元）之间的函数关系为
，且知投入广告费1万元时，可销售2万件产品。预计此种产品的年销售收入
（万元）等于年成本（万元）的150%与年广告费用50%的和。
（1）试将年利润
（万元）表示为年广告费（万元）的函数；
（2）当年广告费多少万元时，使年利润最大？年最大利润是多少万元？
解：（1）年利润
∴
（2）
（万元）
等号当且仅当
，即
，
时成立。
即是年广告费为5万元时，使年利润最大，最大利润26.5万元。
杭高2002年度第一学期期中考试高二数学试卷答案
实验班：
1. A 2. B 3. A 4. C 5. A 6. B 7．A 8． C 9． C 10．B 11．B
12. C 13. B 14. A 15. C
16． __. 17. x
< 1或x > 3 .18. ____8____.
19. ___
____. 20.
__3__
21．直线l的方程为11x – 3y – 6 = 0或17x + 6y – 105 = 0
22．a 
或0 < b 
6.
23．解：（1）直线AC的方程为：5x + y – 25 = 0, x – 5y + 21 = 0
（2）点A的横坐标的取值范围为[3，6]
24．解：（1）年利润
∴
（2）
（万元）
等号当且仅当，即，时成立。
即是年广告费为5万元时，使年利润最大，最大利润26.5万元。