高二数学第一学期期中考试试卷

高二数学第一学期期中考试试卷(实验班)

一、选择题（本大题共10小题，每小题4分，共40分）

1，  直线2x－y=0与x－3=0的夹角为（　）

A　 arctan2　　　　　　　　  B－arctan2　　 C arctan　 D－arctan

2，  不等式（x³－1）(x －1)(x+2)>0 的解集（　）

A {xx>－2}　　　　　　　　　　  B{xx>-2且x≠1}

C{xx<-2或x>1}　　　　　　　　  D{x-2<x<1}

3，若直线x+ay-2=0，与(3a-1)x-ay-1=0平行，则a的值为（　）

A6　　B 1/6　　C　0或6　　　 D　0或1/6

4，若0<a<1,0<b<1则 a+b,,a²+b²,2ab中最大的一个是（　）

A a+b　　　B 　　 C　a²+b²　D　2ab

5，若图中l₁, l₂,l₃,l₄的斜率分别为k₁　k₂　k₃　k₄则（　）

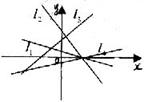A K₃>K₄>K₂>K₁　　　 B K₄>K₃>K₁>K₂

C K₃>K₄>K₁>K₂　　　 D K₄>K₃>K₂>K_1­

6，点p(x₁,y₁)关于直线x+y+1=0对称的点的坐标为

（　）

A （-y₁-1 ,-x₁-1） B　(y₁-1,-x₁-1)　　C　(-y₁+1,-x₁+1)　 D　(y₁+1,x₁+1)

7、A=C≠0B=0是Ax²+Bxy+Cy²+Dx+Ey+F=0表示圆的（　）

A、充分不必要条件　　　　  B、必要不充分条件

C、充要条件　　　　　　　  D、既不充分又不必要条件

8、过椭圆=1（a>b>0）中心的直线与椭圆交于A，B两点，设椭圆焦点分别为F₁(-c,0),F₂(c,0),则四边形面积最大值（　）

A　 ab　　B　2ab　　C　 bc　　　　D 2ab

9，如果椭圆=1的弦被点（4，2）平分，那么这条弦所在直线的方程是（　）

A　x-2y =0　　 B　x+2y-4=0　　C　2x+3y-12=0　D x+2y-8=0

10，我国发射的神州号宇宙飞船的运行轨道是以地心为一个焦点的椭圆，设地球的半径为R，飞船的近地点，远地点距地面分别为r₁,r₂,则飞船运行轨迹短轴长为　（　）

A　2r₁r­_{2­　 ­}　　B r₁r₂　　C2　 D

二，填空题（共四小题，每小题4分，共16分）

13，曲线x=2cosθ　　上的点到直线4x+3y-12=0的距离最大值_____________

　　　  Y=2sinθ　　

14，设F₁，F₂是双曲线=1的焦点，AB是过左焦点F₁的弦，且A，B两点都在左支上，若△ABF₂的周长为30，则AB_________________

15，若椭圆两准线间的距离等于焦距的4倍，则椭圆的离心率为_________

16经过直线2x+y+4=0和圆x²+y²+2x-4y+1=0的两个交点且面积最小的圆的方程________________

三解答题（共五个大题，64分）

17：（12分）一动圆与两定圆C₁：（x+3）²+y²=9和C₂：（x-3）²+y²=1都外切，求动圆圆心p的轨迹方程。

18；（12分）已知椭圆中心在原点，对称轴为坐标轴，椭圆短轴端点B与两焦点F₁，F₂组成三角形的周长为4+2且∠F₁BF₂=120°，求椭圆的方程。

19；（12分）下表给出甲，乙，丙三种食物中维生素A，B的含量及成本

	甲	乙	丙
维生素A（单位/千克）	400	600	400
维生素B（单位/千克）	800	200	400
成本（元/千克）	7	6	5

　营养师想买这三种食物共10千克，使之所含维生素A不少于4400单位，维生素B不少于4800单位，问这三种食物各购买多少时，成本最低，最低成本是我少？

20：（14分）已知点A（）B（），动点C到A，B两点的距离的差的绝对值为2，点C的轨迹与直线y=x-2交于D,　E两点，求线段DE的长

21：（14分）直线y=kx+1与双曲线3x²-y²=1相交于不同的两点A，B

（1）　　　 若以AB为直径的圆恰好过原点，求k的值

（2）　　　 是否存在实数k，使A，B两点关于直线y=2x对称，若存在求k 的范围，若不存在，说明理由。

高二数学其中考试实验班答案

一、BBDAC， ABDDC

二、（13）　（14）9　（15）　　 （16）x²+y²+x-

三、解答题

17解：设动圆圆心P(x,y)p 半径为r

由已知C₁(－3,0)　半径 r₁=3　 C₂(3,0)　　 半径r₂=1

则PC₁=r₁+r=3+r　 PC₂=r₂+r=1+r

∴PC₁－PC₂=（3+r）－(1+r)=2　　  根据双曲线定义

∴P点为以C₁ C₂为焦点的双曲线的右支

∴2a=2　　a=1　 2c=6　c=3　 ∴b²=c²－a²=8

所求P点轨迹方程为（x>0）

18，解由椭圆几何意义可知，△F₁BF₂的周长为BF₁+BF₂+F₁F₂

即a+a+2C=2a+2C=4+2　　 ∴a+c=2+①

∵△F₁BF₂为等腰三角形，顶角F₁BF₂=120°∴∠F₁BO=60°

∴a=　∴C=a　②

由①②可知　a=2　　c=　　 ∴b=1

故所求椭圆方程为或

19,解：设所购甲,乙两种食品分别为x, y千克则丙食物为10-x-y千克成本

 =7x+6y+5(10－x－y)由题意　 x, y满足的线性条件　　　　

为400x+600y+400(10－x－y)≥4400　　 即　　y≥2　　　　　 

　800x+200y+400(10－x－y) ≥4800　　　　2x－y≥4

目标函数=7x+6y+5(10-x-y)=2x+y+50

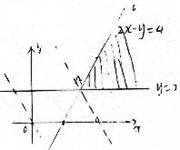
作出上述不等式所确定的平行或如图令2x+y=m　则直线2x+y=m经过平行域中的A点时m最小

而　 y=2

2x-y=4　得A(3　2) ∴_min=2×3+2+50=58

故甲乙丙三种食品各3千克，2千克，5千克是成本最低，最低成本58元

20、解：设点（x .y）则CA－CB=±2　根据双曲线定义可知点C的轨迹方程为双曲线=1　 由2a=2　 a=1　2C=AB=2　 ∴C=　　∴b²=2 故C点轨迹方程为x²－

由x²－

 y=x－2　　得x²+4x-6=0 ∵△=4²+4×6>0 ∴直线与曲线有两交点

设D（x₁,y₁） E(x₂ y₂) 则x₁+x₂=－4　x₁·x₂=－6　故

DE=

（3-k2）x2-2kx-2=0

21、解（1）设A（x₁,y_1­） B(x₂, y₂)则　y=kx+1

　　　　　　　　　　　　　　　　  3x²+y²=1　　　　

由韦达定理　　x₁+x₂=　　　　x­₁·x₂= 　则y₁y₂=(kx₁+1)(kx₂+1)

=k²x₁x₂+k(x₁+x₂)+1=　+K·　 +1=1　 又AB为直径的圆过原点

∵DA⊥OB ∴　x₁x₂+y₁y₂=0　 即　+1=0　 K=±1

（2）假设存在实数使A B两点关于y=2x对称， 则AB中点在y=2x上

由（1）可知中点M（±1　）　 ∴=2·　即K=±

而AB与y=2x垂直∴K_AB=-　与K=±矛盾故假设不成立

∴不存在实数K满足上述条件