高二数学第一学期月考(二)试卷
一、填空题:(4×12=48)
1.设集合![]() 则满足
则满足![]() 的集合C的个数
的集合C的个数
是 。
2.设![]() , b是两个实数,给出下列条件:①
, b是两个实数,给出下列条件:①![]() ②
②![]() ③
③![]() ④
④![]()
⑤![]() ,其中能推出“
,其中能推出“![]() , b中至少有一个数大于
, b中至少有一个数大于
3.方程![]() 的解是 。
的解是 。
4.正三棱锥![]() 中,
中,![]()
![]() ,体积为
,体积为![]() ,则侧棱与底面所成角的大小为
。
,则侧棱与底面所成角的大小为
。
5.从编号为![]() 到
到![]() 的
的![]() 张卡片中任取
张卡片中任取![]() 张,则取出至少有
张,则取出至少有![]() 张是奇数号的概率是
。
张是奇数号的概率是
。
6.若![]() 为非零向量,且
为非零向量,且![]() =
=![]() =
=![]() ,则
,则![]() 与
与![]() 的夹角为 。
的夹角为 。
7.若角![]() 终边落在直线
终边落在直线![]() 上,则
上,则![]() +
+![]() 的值等于 。
的值等于 。
8.对于函数![]() =
=![]() (
(![]() ), 则它的值域为
。
), 则它的值域为
。
9.若三数![]() ,
,![]() ,
, ![]() 成等差数列,且
成等差数列,且![]() 又成等比数列,则
又成等比数列,则![]() 的值为 。
的值为 。
10.一种专门占据内存的计算机病毒,开机时占据内存![]() KB,然后每
KB,然后每![]() 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的![]() 倍,那么开机后经过 分钟,该病毒占据
倍,那么开机后经过 分钟,该病毒占据![]() MB内存(
MB内存(![]() MB=
MB=![]() KB)。
KB)。
11.对任意两个复数![]() 定义运算“*”为
定义运算“*”为![]() ,设非零复数
,设非零复数![]() 在复平内对应点为
在复平内对应点为![]() ,若
,若![]() ,则在△
,则在△![]() 中(
中(![]() 为原点)
为原点)![]()
等于 。
12.设函数![]() 的定义域关于原点对称,且适合下列三个条件:
的定义域关于原点对称,且适合下列三个条件:
①对于定义域内的![]() 都有
都有![]() =
=![]() ; ②存在常数
; ②存在常数![]()
![]() 0,使
0,使![]() ;
;
③对于![]() 有
有![]() 。试求它的一个周期
。
。试求它的一个周期
。
二、选择题:(4×4=16)
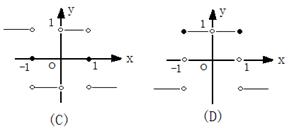
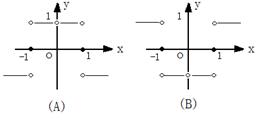 13.函数
13.函数![]() 的大致图象为 ( )
的大致图象为 ( )
14.已知直二面角![]() ,直线
,直线![]() ,直线
,直线![]() ,且
,且![]() 与
与![]() 不垂直,
不垂直,![]() 与
与![]() 不垂直,那么( )
不垂直,那么( )
A.![]() 与
与![]() 可能垂直,但不可能平行 B.
可能垂直,但不可能平行 B.![]() 与
与![]() 可能垂直,也可能平行
可能垂直,也可能平行
C.![]() 与
与![]() 不可能垂直,不可能平行
D.
不可能垂直,不可能平行
D.![]() 与
与![]() 不可能垂直,但可能平行
不可能垂直,但可能平行
15.若函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的范围是
( )
的范围是
( )
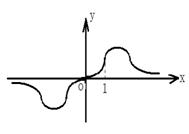 |
A.![]() B.(0,3)
B.(0,3)
C.(1,3) D.(2,3)
16.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示。某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
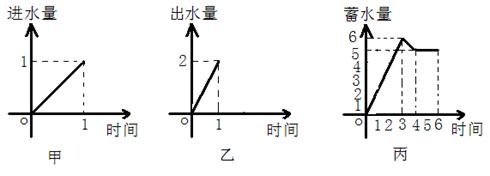 |
给出以下![]() 个论断:
个论断:
①![]() 点到
点到![]() 点只进水不出水;②
点只进水不出水;②![]() 点到
点到![]() 点不进水只出水;③
点不进水只出水;③![]() 点到
点到![]() 点不进水不出水。
点不进水不出水。
则一定确定的论断是: ( )
A.① B.①② C.①③ D.①②③
三、解答题:(12+12+14+14+16+18)
17.设函数![]()
①求证:![]() 能表示成一个奇函数
能表示成一个奇函数![]() 和一个偶函数
和一个偶函数![]() 的和,并求出
的和,并求出![]() 和
和![]() 的表达式;
的表达式;
②若![]() 和
和![]() 在区间
在区间![]() 上均是减函数,求
上均是减函数,求![]() 的取值范围。
的取值范围。
18.有关于![]() 的一元二次方程
的一元二次方程![]() -(
-(![]() +i)
+i)![]() -(2+i)=0(
-(2+i)=0(![]() ,
,![]()
![]()
![]() )
)
①若此方程有一实数根,求锐角![]() 的值;
的值;
②求证:对任意的实数的![]() ,原方程不可能有纯虚数根。
,原方程不可能有纯虚数根。
19.正三棱柱![]() 所有棱长均为4,
所有棱长均为4,![]() 是
是![]() 的中点,
的中点,![]() 是侧棱
是侧棱![]() 上的一点,
上的一点,![]()
①建立适当的坐标系,求![]() 点的坐标;
点的坐标;
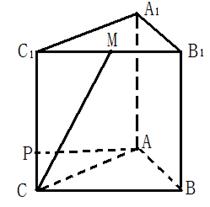 ②求
②求![]() 与底面
与底面![]() 所成角的大小。
所成角的大小。
20.已知数列![]() ,前
,前![]() 项和
项和
![]()
①判断两数列各是什么数列,并求出它们的通项公式;
②能否找到一个不为![]() 的整数
的整数![]() 使
使![]() 为常数?若找不到,请说明理由;若能找到,试求
为常数?若找不到,请说明理由;若能找到,试求![]() 与这个常数。
与这个常数。
21.某租赁公司拥有汽车![]() 辆,当每辆车的月租金为
辆,当每辆车的月租金为![]() 元时,可全部租出,当每辆车的月租金每增加
元时,可全部租出,当每辆车的月租金每增加![]() 元时,未租出的车将会增加一辆,租出的车每辆每月需维护费
元时,未租出的车将会增加一辆,租出的车每辆每月需维护费![]() 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费![]() 元
元
①当每辆车的月租金定为![]() 元时,能租出多少辆车?
元时,能租出多少辆车?
②当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
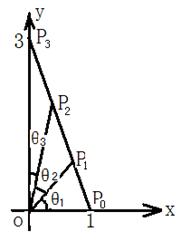 22.已知两点
22.已知两点![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的两点 设
上的两点 设![]()
![]() =
=![]() ,
,![]()
![]()
![]() ,
, ![]()
![]() ,
,
①若![]() 为线段
为线段![]() 的三等分点,求:
的三等分点,求:![]() ,
,![]() ,
,![]() 的值;
的值;
②若![]() ,求
,求![]() 两点的坐标。
两点的坐标。
松江一中2003学年第一学期月考(二)试卷
一、填空题:(4×12=48)
1.设集合![]() 则满足
则满足![]() 的集合C的个数是
的集合C的个数是 ![]() 。
。
2.设![]() , b是两个实数,给出下列条件:①
, b是两个实数,给出下列条件:①![]() ②
②![]() ③
③![]() ④
④![]()
⑤![]() ,其中能推出“
,其中能推出“![]() , b中至少有一个数大于
, b中至少有一个数大于
3.方程![]() 的解是
的解是 ![]() 。
。
4.正三棱锥![]() 中,
中,![]()
![]() ,体积为
,体积为![]() ,则侧棱与底面所成角的大小为
,则侧棱与底面所成角的大小为 ![]() 。
。
5.从编号为![]() 到
到![]() 的
的![]() 张卡片中任取
张卡片中任取![]() 张,则取出至少有
张,则取出至少有![]() 张是奇数号的概率是
张是奇数号的概率是 ![]() 。
。
6.若![]() 为非零向量,且
为非零向量,且![]() =
=![]() =
=![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为 ![]() 。
。
7.若角![]() 终边落在直线
终边落在直线![]() 上,则
上,则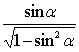 +
+![]() 的值等于
的值等于 ![]() 。
。
8.对于函数![]() =
=![]() (
(![]() ), 则它的值域为
), 则它的值域为 ![]() 。
。
9.若三数![]() ,
,![]() ,
, ![]() 成等差数列,且
成等差数列,且![]() 又成等比数列,则
又成等比数列,则![]() 的值为
的值为 ![]() 。
。
10.一种专门占据内存的计算机病毒,开机时占据内存![]() KB,然后每
KB,然后每![]() 分钟自身复制一次,复制后所占内存是原来的
分钟自身复制一次,复制后所占内存是原来的![]() 倍,那么开机后经过
倍,那么开机后经过 ![]() 分钟,该病毒占据
分钟,该病毒占据![]() MB内存(
MB内存(![]() MB=
MB=![]() KB)。
KB)。
11.对任意两个复数![]() 定义运算“*”为
定义运算“*”为![]() ,设非零复数
,设非零复数![]() 在复平内对应点为
在复平内对应点为![]() ,若
,若![]() ,则在△
,则在△![]() 中(
中(![]() 为原点)
为原点)![]()
等于 ![]() 。
。
12.设函数![]() 的定义域关于原点对称,且适合下列三个条件:
的定义域关于原点对称,且适合下列三个条件:
①对于定义域内的![]() 都有
都有![]() =
=![]() ; ②存在常数
; ②存在常数![]()
![]() 0,使
0,使![]() ;
;
③对于![]() 有
有![]() 。试求它的一个周期
。试求它的一个周期 ![]() 。
。
二、选择题:(4×4=16)
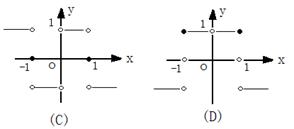
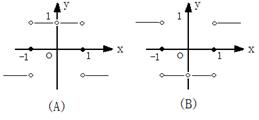 13.函数
13.函数![]() 的大致图象为 ( A )
的大致图象为 ( A )
14.已知直二面角![]() ,直线
,直线![]() ,直线
,直线![]() ,且
,且![]() 与
与![]() 不垂直,
不垂直,![]() 与
与![]() 不垂直,那么( D )
不垂直,那么( D )
A.![]() 与
与![]() 可能垂直,但不可能平行 B.
可能垂直,但不可能平行 B.![]() 与
与![]() 可能垂直,也可能平行
可能垂直,也可能平行
C.![]() 与
与![]() 不可能垂直,不可能平行
D.
不可能垂直,不可能平行
D.![]() 与
与![]() 不可能垂直,但可能平行
不可能垂直,但可能平行
15.若函数![]() 的图象如图所示,则
的图象如图所示,则![]() 的范围是
( C )
的范围是
( C )
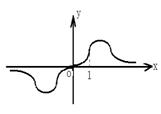 |
A.![]() B.(0,3)
B.(0,3)
C.(1,3) D.(2,3)
16.一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示。某天0点到6点,该水池的蓄水量如图丙所示。(至少打开一个水口)
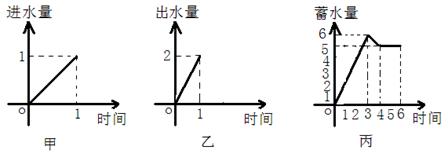 |
给出以下![]() 个论断:
个论断:
①![]() 点到
点到![]() 点只进水不出水;②
点只进水不出水;②![]() 点到
点到![]() 点不进水只出水;③
点不进水只出水;③![]() 点到
点到![]() 点不进水不出水。
点不进水不出水。
则一定确定的论断是: ( A )
A.① B.①② C.①③ D.①②③
三、解答题:(12+12+14+14+16+18)
17.设函数![]()
①求证:![]() 能表示成一个奇函数
能表示成一个奇函数![]() 和一个偶函数
和一个偶函数![]() 的和,并求出
的和,并求出![]() 和
和![]() 的表达式;
的表达式;
②若![]() 和
和![]() 在区间
在区间![]() 上均是减函数,求
上均是减函数,求![]() 的取值范围。
的取值范围。
解:① ![]()
② 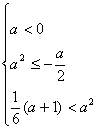 ,
,![]()
18.有关于![]() 的一元二次方程
的一元二次方程![]() -(
-(![]() +i)
+i)![]() -(2+i)=0(
-(2+i)=0(![]() ,
,![]()
![]()
![]() )
)
①若此方程有一实数根,求锐角![]() 的值;
的值;
②求证:对任意的实数的![]() ,原方程不可能有纯虚数根。
,原方程不可能有纯虚数根。
解:① 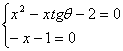 ,
,![]()
② 设![]() ,则
,则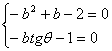 ,
,![]()
19.正三棱柱![]() 所有棱长均为4,
所有棱长均为4,![]() 是
是![]() 的中点,
的中点,![]() 是侧棱
是侧棱![]() 上的一点,
上的一点,![]()
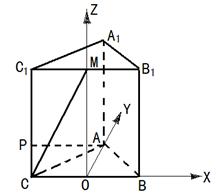 ①建立适当的坐标系,求
①建立适当的坐标系,求![]() 点的坐标;
点的坐标;
②求![]() 与底面
与底面![]() 所成角的大小。
所成角的大小。
解:① ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
② ![]()
![]()
20.已知数列![]() ,前
,前![]() 项和
项和
![]()
①判断两数列各是什么数列,并求出它们的通项公式;
②能否找到一个不为![]() 的整数
的整数![]() 使
使![]() 为常数?若找不到,请说明理由;若能找到,试求
为常数?若找不到,请说明理由;若能找到,试求![]() 与这个常数。
与这个常数。
解:① ![]() ,
,![]()
② ![]()
![]() ,
,![]() ,
,![]()
![]()
21.某租赁公司拥有汽车![]() 辆,当每辆车的月租金为
辆,当每辆车的月租金为![]() 元时,可全部租出,当每辆车的月租金每增加
元时,可全部租出,当每辆车的月租金每增加![]() 元时,未租出的车将会增加一辆,租出的车每辆每月需维护费
元时,未租出的车将会增加一辆,租出的车每辆每月需维护费![]() 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费![]() 元
元
①当每辆车的月租金定为![]() 元时,能租出多少辆车?
元时,能租出多少辆车?
②当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:① ![]() 辆
辆
② 月租金定为![]() 元,月收益为
元,月收益为![]() 元
元
![]()
月租金定为![]() 元,最大月收益是
元,最大月收益是![]() 元。
元。
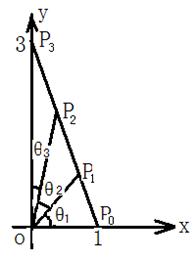 22.已知两点
22.已知两点![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的两点 设
上的两点 设![]()
![]() =
=![]() ,
,![]()
![]()
![]() ,
, ![]()
![]() ,
,
①若![]() 为线段
为线段![]() 的三等分点,求:
的三等分点,求:![]() ,
,![]() ,
,![]() 的值;
的值;
②若![]() ,求
,求![]() 两点的坐标。
两点的坐标。
解:① ![]()
![]()
![]()
②
![]()
![]()