直线和平面平行

　　　　　  高二数学期末复习讲义（3）　　

直线和平面平行

一．复习目标：

1．了解直线和平面的位置关系；掌握直线和平面平行的判定定理和性质定理．

二、基础知识：

1、直线和平面的位置关系有＿＿＿＿＿＿＿＿＿＿＿＿，符号表示：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

２　线面平行判断定理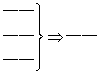　　性质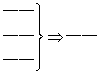

　判断和证明线面平行的方法有：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

　怎样转化＂线面平行＂：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿

二．课前预习：

1．已知直线、和平面，那么的一个必要不充分的条件是　　　 （ 　 ）

，　　　　　　　 　　　，

且　　　　　　　　　  、与成等角

2．　若直线l与平面α的一条平行线平行，则l和α的位置关系是　　　　　　　  (　　 )

　 A　　　　　B 　　　　 C 　　　 D

3. E、F、G分别是四面体ABCD的棱BC、CD、DA的中点，则此四面体中与过E、F、G的截面平行的棱的条数是　　　　　　　　　　　　　　　　　　　　　　 

　 A．0　　　　　  B 1　　　　　　  C 2　　　　　　　　　 D3

4．空间四边形的两条对角线，，则平行于两对角线的截面四边形的周长的取值范围是　　　　　　　 ．　

三．例题分析：

例1　18．已知P、Q是单位正方体ABCD-A₁B₁C₁D₁的面AA₁D₁D、面A₁B₁C₁D₁中心。　

（1）　　　 求线段PQ的长；

（２）证明：PQ//平面AA₁B₁B

小结：

例2．如图，已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点．

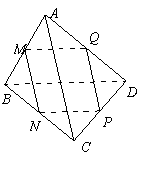求证：(1)线段MP和NQ相交且互相平分；(2)AC∥平面MNP，BD∥平面MNP．

证明：　

　

小结：

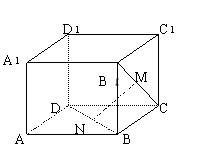
例３．如图，正方形ABCD-ABCD中，点N在BD上，点M在BC上，且CM=DN，求证：MN∥平面A A BB．

小结：

四．课后作业： 　　　　　　　　　　　　　班级　　　学号　　　姓名　　　　　 

1．设线段是夹在两平行平面间的两异面线段，点，，若分别为的中点，则有　　　　 （ 　 ）　　　　　　　　　

　　　　　　　 

　　　　　　　 

2．下列各命题：

（1）　　　 经过两条平行直线中一条直线的平面必平行于另一条直线；

（2）　　　 若一条直线平行于两相交平面，则这条直线和交线平行；

（3）　　　 空间四边形中三条边的中点所确定平面和这个空间四边形的两条对角线都平行。

 其中假命题的个数为　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

A　0　　　　　 B 1　　　　　　  C 2　　　　　　　　　 D 3

3．在正四棱柱中，分别为棱、、、的中点，是的中点，点在四边形及其内部运动，则满足条件　　　　

时，有平面．　）

4．在长方体中，经过其对角线的平面分别与棱、相交于两点，则四边形的形状为　　　　　　  ．（　

5．．判断下列命题是否正确：

(1)过平面外一点可作无数条直线与这个平面平行　　　　　　　　　　  　　 (　　)

(2)若直线，则l不可能与α内无数条直线相交　　　　　　　　　　　  (　　)

(3)若直线l与平面α不平行，则l与α内任一直线都不平行　　　　　　　　  (　　)

(4)经过两条平行线中一条直线的平面平行于另一条直线　　　　　　　  　　 (　　)

(5)若平面α内有一条直线和直线l异面，则　　　　　　　　　　　　  (　　)

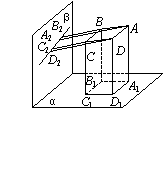６．如图，A，B，C，D四点都在平面a，b外，它们在a内的射影A₁，B₁，C₁，D₁是平行四边形的四个顶点，在b内的射影A₂，B₂，C₂，D₂在一条直线上，求证：ABCD是平行四边形．

证明：　

　

6．若一直线与一个平面平行，则过平面内的一点且与这条直线平行的直线必在此平面内．

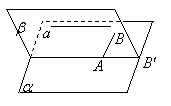解：　

7. 用平行于四面体ABCD的一组对棱AB、CD的平面截此四面体

(1)求证：所得截面MNPQ是平行四边形；

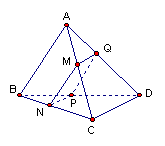(2)如果AB=CD=a，求证：四边形MNPQ的周长为定值。