直线和圆的方程本章综合训练
一、选择题（每小题的四个选项中，只有一项符合题目要求）
1．若直线
不经过第一象限，则实数m的取值范围是（ ）
A．
B．
C．
D．
2．如果直线l沿x负方向平移3个单位，再沿y轴正方向平移1个单位后，又回到原来的位置，那么直线l的斜率为（ ）
A．
B．-3
C．
D．3
3．已知两点A（0，1），B（1，0），若直线y=k(x+1)与线段AB总有公共点，则k的取值范围是（ ）
A．[-1，1]
B．[0，1]
C．[-1，0]
D．[0，+∞]
4．已知直线2x+y-2=0和mx-y+1=0的夹角为45°，那么m的值为（ ）
A．或-3
B．或3
C．或3
D．或-3
5．方程
表示圆，则a的取值范围是（ ）
A．a<-2或
B．
C．-2<a<0
D．
6．两圆
，
的公切线有（ ）
A．2条
B．3条
C．4条
D．以上都不对
7．若圆
上有且只有两个点到直线4x-3y=2的距离等于1，则半径r的取值范围是（ ）
A．（4，6）
B．[4，6）
C．（4，6]
D．[4，6]
8．如果直线y=ax+2与直线y=3x-b关于直线y=x对称，那么（ ）
A．
，b=-6
B．，b=6
C．a=3，b=-2
D．a=3，b=6
9．圆
关于直线x+y=2对称的充要条件是（ ）
A．D+E+2=0
B．D+E+4=0
C．D+E=2
D．D+E=4
10．参数方程：
表示的图形是（ ）
A．圆心为（-3，3），半径为9的圆
B．圆心为（-3，3），半径为3的圆
C．圆心为（3，-3），半径为9的圆
D．圆心为（3，-3），半径为3的圆
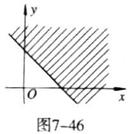
11．图7-46中表示的平面区域满足不等式（ ）
A．x+y-1>0
B．x+y-1≥0
C．x+y-1≤0
D．x+y-1<0
12．已知x、y的约束条件是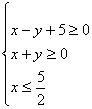
则f(x，y)=2x+4y的最小值为（ ）
A．5
B．-5
C．10
D．-10
二、填空题
13．过点（10，-4）且倾斜角的正弦是
的直线方程是___________。
14．过点（2，1）且在两条坐标轴上截距相等的直线方程是___________。
15．在△ABC中，A（2，4），B（-1，2），C（1，0），若Q（x，y）在△ABC内部和边界上运动，那么函数z=x-y的最大值为___________。
16．过点P（6，4）且被圆
截得长为
的弦所在直线方程为___________。
三、解答题
17．求经过点（2，-1），倾斜角为直线4x+3y-1=0的倾斜角的一半的直线方程。
18．直线y=2x是△ABC中∠C的平分线所在的直线，若A、B坐标分别是
，
，求点C的坐标，并判断△ABC的形状。
19．三角形三个顶点为A(1，a)，B(-1，0)，C(2a，1)(1)求满足条件
的动点P的轴迹方程；
（2）求上述曲线通过线段AB中点的充要条件。
20．圆与y轴相切，圆心在直线x-3y=0上，且在直线y=x上截得的弦长为
，求此圆的方程。
21．若直线xcosθ+ysinθ=2(θ∈[0，π]与曲线
有公共点，求θ的取值范围。
22．将两种大小不同的钢板截成A、B、C三种不同规格的小钢板，第一种钢板可截得A、B、C三种不同规格的小钢板块数分别1、2、1；第二种钢板可截得A、B、C三种不同规格的小钢板块数分别为1、1、3。每张钢板的面积第一种为
，第二种为
，今需要A、B、C三种规格的小钢板成品各为12块、15块、27块。问各截这两种钢板多少张，可得所需三种规格的成品且所用钢板面积最小？
答案与提示
一、1．D
2．A
3．B
4．C
5．D
6．A
7．A
8．B
9．B
10．D
11．B
12．B
二、13．5x-12y-98=0或5x+12y-2=0
14．x+y=3或
15．
16．x-y-2=0或7x-17y+26=0
三、17．2x-y-5=0。 提示：用点斜式。 求斜率时可用半角的正切公式或万能公式，同时要注意倾斜角的范围。
18．C（2，4），△ABC是以∠C为直角的直角三角形。 提示：用到角公式。通过斜率求点C的坐标；用三边的斜率判定该三角形是直角三角形。
19．（1）
（2）所求的充要充件为a=0或
20．所求圆的方程为
或
21．
。 提示：通过判别式建立关于θ的不等式
22．应截取第一种钢板4张，第二种钢板8张，得所需A、B、C三种规格的钢板且所使用的面积最小